Cicle (permutació)

En matemàtiques, i en particular en teoria de grups, una permutació cíclica és una permutació dels elements d'un conjunt X que transforma els elements d'un subconjunt S de X els uns en els altres de manera cíclica, mentre que manté fixos (és a dir, transforma en ells mateixos) la resta d'elements de X. Per exemple, la permutació de {1, 2, 3, 4} que envia 1 a 2, 2 a 3, 3 a 4 i 4 a 1 és un cicle, mentre que la permutació que envia 1 a 3, 3 a 1, 2 a 4 i 4 a 2 no ho és (permuta de manera separada els parells {1, 3} i {2, 4}).

Un cicle d'una permutació és un subconjunt dels elements que s'intercanvien de forma cíclica. El conjunt S s'anomena òrbita del cicle. Tota permutació d'un nombre finit d'elements es pot descompondre en un nombre finit de cicles amb òrbites disjuntes. En alguns contextos, hom anomena cicle a una permutació cíclica.

Definició

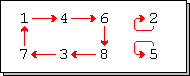
Hom diu que una permutació és una permutació cíclica si i només si consisteix d'un sol cicle no trivial (un cicle de longitud > 1).^[1]

Exemple:

${\displaystyle {\begin{aligned}&{\begin{pmatrix}1&2&3&4&5&6&7&8\\4&2&7&6&5&8&1&3\end{pmatrix}}&=\\=&{\begin{pmatrix}1&4&6&8&3&7&2&5\\4&6&8&3&7&1&2&5\end{pmatrix}}&=\\=&(146837)(2)(5)\end{aligned}}}$

(1)

Alguns autors restringeixen la definició a aquelles permutacions que tenen exactament un cicle (és a dir, no s'hi permeten punts fixos).^[2]

Exemple:

${\displaystyle {\begin{aligned}&{\begin{pmatrix}1&2&3&4&5&6&7&8\\4&5&7&6&8&2&1&3\end{pmatrix}}&=\\=&{\begin{pmatrix}1&4&6&2&5&8&3&7\\4&6&2&5&8&3&7&1\end{pmatrix}}&=\\=&(14625837)\end{aligned}}}$

(2)

Més formalment, hom diu que una permutació d'un conjunt X, que és una funció bijectiva ${\displaystyle \sigma :X\to X}$, és un cicle si l'acció sobre X del subgrup generat per ${\displaystyle \sigma }$ té com a màxim una òrbita amb més d'un element.^[3] Aquest concepte s'usa sobretot si X és un conjunt finit; en aquest cas, és evident que l'òrbita més gran, S, també és finita. Sigui ${\displaystyle s_{0}}$ un element qualsevol de S, i escrivim ${\displaystyle s_{i}=\sigma ^{i}(s_{0})\,}$ per a qualsevol ${\displaystyle i\in \mathbf {Z} }$. Si S és finit, llavors existeix un nombre mínim ${\displaystyle k\geq 1}$ tal que ${\displaystyle s_{k}=s_{0}}$. Aleshores ${\displaystyle S=\{s_{0},s_{1},\ldots ,s_{k-1}\}}$, i ${\displaystyle \sigma }$ és la permutació definida per

${\displaystyle \sigma (s_{i})=s_{i+1}\quad {\mbox{per }}0\leq i<k}$

i ${\displaystyle \sigma (x)=x}$ per a qualsevol element de ${\displaystyle X\setminus S}$. Els elements que no queden fixats per ${\displaystyle \sigma }$ es poden visualitzar com

${\displaystyle s_{0}\mapsto s_{1}\mapsto s_{2}\mapsto \cdots \mapsto s_{k-1}\mapsto s_{k}=s_{0}}$.

Hom pot escriure un cicle emprant la notació de cicles compacta ${\displaystyle \sigma =(s_{0}~s_{1}~\dots ~s_{k-1})}$ (notem que no hi ha comes entre els elements, per evitar confusions amb una k-tupla). La longitud d'un cicle és el nombre d'elements de la seva òrbita més gran. Un cicle de longitud k també es diu k-cicle.

Hom diu que l'òrbita d'un 1-cicle és un punt fix de la permutació, però pensat com a permutació, tot 1-cicle és la permutació identitat.^[4] Quan s'utilitza la notació de cicles, hom acostuma a suprimir els 1-cicles, si no hi ha confusió.^[5]

Propietats bàsiques

Un dels resultats bàsics dels grups simètrics estableix que tota permutació es pot expressar com a producte de cicles disjunts (més precisament: cicles amb òrbites disjuntes); aquests cicles disjunts commuten els uns amb els altres, i l'expressió de la permutació és única llevat de l'ordre dels cicles (observem, però, que la notació de cicles no és única: cada k-cicle es pot escriure de k maneres diferents, depenent de l'elecció de ${\displaystyle s_{0}}$ en la seva òrbita).^[6] Per tant, el multiconjunt de les longituds dels cicles expressats d'aquesta forma (l'indicador de cicles) està unívocament determinat per la permutació, i també determina tant la signatura com la classe de conjugació de la permutació del grup simètric.^[7]

El nombre de k-cicles del grup simètric S_n ve donat, per ${\displaystyle 1\leq k\leq n}$, per les següents fórmules equivalents:

${\displaystyle {\begin{aligned}{\binom {n}{k}}(k-1)!&={\frac {n(n-1)\cdots (n-k+1)}{k}}\\&={\frac {n!}{(n-k)!k}}\end{aligned}}}$

Un k-cicle té signatura (−1)^{k − 1}.

Transposicions

Una transposició és un cicle amb dos elements. Per exemple, la permutació de {1, 2, 3, 4} que envia 1 a 1, 2 a 4, 3 a 3 i 4 a 2 és una transposició (la transposició que intercanvia 2 i 4).

Propietats

Qualsevol permutació es pot expressar com a composició (producte) de transposicions; formalment, les transposicions són generadores del grup.^[8] De fet, si hom pren ${\displaystyle a=1}$, ${\displaystyle b=2}$, ..., ${\displaystyle e=5}$, llavors qualsevol permutació es pot expressar com a producte de transposicions adjacents, és a dir, com a transposicions de la forma ${\displaystyle (k~~k+1)}$; en aquest cas, ${\displaystyle (1~2)}$, ${\displaystyle (2~3)}$, ${\displaystyle (3~4)}$ i ${\displaystyle (4~5)}$. Això és una conseqüència del fet que qualsevol transposició es pot expressar com a producte de transposicions adjacents. Concretament, hom pot expressar la transposició ${\displaystyle (k~~l)}$ on ${\displaystyle k<l}$ movent k a la posició de l un pas a cada iteració, i llavors movent l a la posició original de k, la qual cosa intercanvia aquests dos elements i no realitza cap més canvi:

${\displaystyle (k~~l)=(k~~k+1)\cdot (k+1~~k+2)\cdots (l-1~~l)\cdot (l-2~~l-1)\cdots (k~~k+1)}$.

La descomposició d'una permutació en producte de transposicions s'obté, per exemple, escrivint la permutació com a producte de cicles disjunts, i després separant iterativament cadascun dels cicles de longitud ≥3 en producte d'una transposició i un cicle de longitud igual a la longitud del cicle original menys 1:

${\displaystyle (a~b~c~d~\ldots ~y~z)=(a~b)\cdot (b~c~d~\ldots ~y~z)}$

Això significa que l'objectiu inicial és moure ${\displaystyle a}$ cap a ${\displaystyle b}$, ${\displaystyle b}$ cap a ${\displaystyle c}$, ${\displaystyle y}$ cap a ${\displaystyle z}$ i finalment ${\displaystyle z}$ cap a ${\displaystyle a}$. En comptes d'això, es poden desplaçar els elements mantenint ${\displaystyle a}$ al seu lloc, primer executant el factor dret (de la manera habitual en la notació d'operadors, i seguint la convenció de l'article Permutació). Amb aquesta operació hem aconseguit moure ${\displaystyle z}$ a la posició de ${\displaystyle b}$, de tal manera que, després de la primera permutació, els elements ${\displaystyle a}$ i ${\displaystyle z}$ encara no estan a les seves posicions finals. La transposició ${\displaystyle (a~b)}$, executada a continuació, identifica l'element ${\displaystyle z}$ mitjançant l'índex de ${\displaystyle b}$, per tal d'intercanviar el que inicialment eren ${\displaystyle a}$ i ${\displaystyle z}$.

Un dels resultats principals sobre grups simètrics afirma que o bé totes les descomposicions d'una permutació donada tenen un nombre parell de transposicions, o bé tenen totes un nombre senar de transposicions.^[9] Això permet que la paritat d'una permutació sigui un concepte ben definit (és a dir, no hi ha ambigüitat possible, perquè davant de dues descomposicions diferents, són ambdues o bé parelles o bé senars).

Referències

Bibliografia

• Anderson, Marlow; Feil, Todd. A First Course in Abstract Algebra. 2a edició. Chapman & Hall/CRC, 2005). ISBN 1-58488-515-7. 
• Fraleigh, John. A first course in abstract algebra. 5a edició. Addison Wesley, 1993. ISBN 978-0-201-53467-2. 
• Rotman, Joseph J. A First Course in Abstract Algebra with Applications. 3a edició. Prentice-Hall, 2006. ISBN 978-0-13-186267-8. 
• Sagan, Bruce E. The Symmetric Group / Representations, Combinatorial Algorithms & Symmetric Functions. Wadsworth & Brooks/Cole, 1991. ISBN 978-0-534-15540-7. 

Enllaços externs

• Permutations as a Product of Transpositions

Aquest article conté material de la pàgina cycle a PlanetMath, llicenciat sota la Llicència de Creative Commons Reconeixement i Compartir-Igual.

Viccionari