Abbildungsklassengruppe

Die Abbildungsklassengruppe eines Raumes ist die Gruppe der „Symmetrien“ (Klassen von Abbildungen) dieses Raumes. Dabei werden Abbildungen, die sich stetig ineinander deformieren lassen, als jeweils eine Klasse von Abbildungen angesehen.

Formaler betrachtet man alle Homöomorphismen (stetige Selbstabbildungen, die eine stetige Umkehrabbildung besitzen) ${\displaystyle f\colon S\to S}$ eines Raumes ${\displaystyle S}$. Man sagt, dass zwei Homöomorphismen ${\displaystyle f_{0},f_{1}}$ zur selben Isotopieklasse gehören bzw. isotop sind, wenn es eine stetige Abbildung ${\displaystyle F\colon S\times \left[0,1\right]\to S}$ mit ${\displaystyle F(s,i)=f_{i}(s)}$ für alle ${\displaystyle s\in S}$ und ${\displaystyle i\in \left\{0,1\right\}}$ gibt. Diese Isotopieklassen von Homöomorphismen bilden mit der (wohldefinierten) Verknüpfung von Homöomorphismen eine Gruppe und diese wird als Abbildungsgruppe ${\displaystyle \operatorname {Mod} (S)}$ oder ${\displaystyle \operatorname {MCG} (S)}$ bezeichnet.

Im Kontext orientierbarer Mannigfaltigkeiten betrachtet man nur die Isotopieklassen orientierungserhaltender Homöomorphismen. (Die Gruppe aller Isotopieklassen wird dann als erweiterte Abbildungsklassengruppe bezeichnet.) Im Fall von Mannigfaltigkeiten mit Rand betrachtet man nur diejenigen Homöomorphismen, die den Rand punktweise fest lassen und erlaubt auch nur solche Isotopien. Man kann dann also formal definieren

${\displaystyle \operatorname {Mod} (S):=\pi _{0}(\operatorname {Homeo} ^{+}(S,\partial S))}$,

wobei ${\displaystyle \operatorname {Homeo} ^{+}(S,\partial S))}$ die kompakt-offene Topologie trägt und ${\displaystyle \pi _{0}}$ die ${\displaystyle 0}$-te Homotopiemenge (also die Menge der Wegzusammenhangskomponenten) bezeichnet.

Meist, insbesondere in gruppentheoretischem Kontext, sind Abbildungsklassengruppen von orientierbaren Flächen gemeint, wenn von „Abbildungsklassengruppen“ die Rede ist.^[1]

Dieser Artikel behandelt im Weiteren ausschließlich Abbildungsklassengruppen von orientierbaren Flächen.

Beispiele

Kreisscheibe

Aus dem Alexander-Trick folgt ${\displaystyle \operatorname {Mod} (D^{2})=0}$: jede den Rand punktweise festlassende Selbstabbildung der Kreisscheibe ist homotop zur Identitätsabbildung.

Sphäre

Ebenfalls aus dem Alexander-Trick folgt ${\displaystyle \operatorname {Mod} (S^{2})=0}$: jede Selbstabbildung der Sphäre ist homotop zur Identitätsabbildung.

Hose

Die Abbildungsklassengruppe der Hose ist ebenfalls trivial. Falls man den Rand nicht notwendig festlassende Abbildungen betrachtet, bekommt man als Abbildungsklassengruppe die symmetrische Gruppe ${\displaystyle \Sigma _{3}}$.

Kreisring

Die Abbildungsklassengruppe des Kreisringes ist zyklisch von unendlicher Ordnung, ein Erzeuger ist der Dehn-Twist an der Kernkurve.

Torus

Die Abbildungsklassengruppe des Torus ist die modulare Gruppe: ${\displaystyle \operatorname {Mod} (T^{2})=\operatorname {SL} (2,\mathbb {Z} )}$. Dasselbe gilt für den Torus mit Loch.^[2]

Flächen höheren Geschlechts

Für ${\displaystyle S\not =S^{2},\mathbb {R} ^{2},D^{2},T^{2}}$ sind die Zusammenhangskomponenten von ${\displaystyle \operatorname {Homeo} ^{+}(S,\partial S)}$ zusammenziehbar, also ${\displaystyle \operatorname {Homeo} ^{+}(S,\partial S)}$ homotopieäquivalent zu ${\displaystyle \operatorname {Mod} (S)}$. (Hamstrom)

Weil die Abbildungsklassengruppen von Sphäre, Kreisscheibe, Kreisring und Torus leicht zu beschreiben sind, werden wir uns in diesem Artikel im Weiteren nur mit den Abbildungsklassengruppen von Flächen negativer Euler-Charakteristik ${\displaystyle \chi (S)<0}$ befassen.

Präsentierungen der Abbildungsklassengruppe

Erzeuger

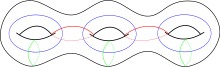
Die Abbildungsklassengruppe einer Fläche wird von Dehn-Twists erzeugt. Wie Lickorish bewiesen hat, genügen die Dehn-Twists an den 3g-1 im Bild rechts dargestellten Kurven, um die Abbildungsklassengruppe zu erzeugen. Ein anderes Erzeugendensystem mit nur 2g-1 Dehn-Twists wurde von Humphries angegeben.

Relationen

Es gibt eine Reihe von Relationen zwischen Dehn-Twists. Im Folgenden listen wir einige Beispiele, wobei ${\displaystyle \tau _{\alpha }}$ jeweils den Dehn-Twist an der Kurve ${\displaystyle \alpha }$ und

${\displaystyle i(\alpha ,\beta ):=\min \left\{\mid \alpha ^{\prime }\cap \beta ^{\prime }\mid \colon \alpha ^{\prime }\ {\mbox{isotop zu}}\ \alpha ,\beta ^{\prime }\ {\mbox{isotop zu}}\ \beta ,\alpha ^{\prime }\pitchfork \beta ^{\prime }\right\}}$

die geometrische Schnittzahl der Kurven ${\displaystyle \alpha ,\beta }$ bezeichnet.

Disjunkt-Relation: Wenn die Schnittzahl ${\displaystyle i(\alpha ,\beta )=0}$ ist, dann ${\displaystyle \left[\tau _{\alpha },\tau _{\beta }\right]=1}$.

Zopf-Relation: Wenn die Schnittzahl ${\displaystyle i(\alpha ,\beta )=1}$ ist, dann ${\displaystyle \tau _{\alpha }\tau _{\beta }\tau _{\alpha }=\tau _{\beta }\tau _{\alpha }\tau _{\beta }}$.

Laternen-Relation: Wenn 7 Kurven wie im Bild rechts angeordnet sind, dann gilt ${\displaystyle \tau _{A}\tau _{B}\tau _{C}=\tau _{R}\tau _{S}\tau _{T}\tau _{U}}$, wobei ${\displaystyle A,B,C}$ die im Bild blauen und ${\displaystyle R,S,T,U}$ die im Bild roten Kurven bezeichnet.

Andererseits gilt für ${\displaystyle i(\alpha ,\beta )\not \in \left\{0,1\right\}}$, dass die Dehn-Twists ${\displaystyle \tau _{\alpha },\tau _{\beta }}$ eine freie Gruppe erzeugen.

Präsentierungen

Es gibt verschiedene Möglichkeiten, explizite Präsentierungen der Abbildungsklassengruppen anzugeben, beispielsweise die Wajnryb-Präsentierung oder die Gervais-Präsentierung.

Zum Beispiel hat ${\displaystyle \operatorname {Mod} (S_{1})=\operatorname {Mod} (T^{2})}$ die Präsentierung ${\displaystyle \operatorname {Mod} (T^{2})=\langle \tau _{l},\tau _{m}\mid \tau _{\alpha }\tau _{\beta }\tau _{\alpha }=\tau _{\beta }\tau _{\alpha }\tau _{\beta },(\tau _{\alpha }\tau _{\beta })^{6}=1\rangle }$ und ${\displaystyle \operatorname {Mod} (S_{2})}$ hat die Birman-Hilden-Präsentierung.

Algebraische Eigenschaften der Abbildungsklassengruppen

Das Zentrum von ${\displaystyle \operatorname {Mod} (S_{g})}$ ist trivial für ${\displaystyle g\geq 3}$.

Die erste Gruppenhomologie ${\displaystyle H_{1}(\operatorname {Mod} (S_{g});\mathbb {Z} )}$ ist trivial für ${\displaystyle g\geq 3}$. Für ${\displaystyle g=2}$ hat man ${\displaystyle H_{1}(\operatorname {Mod} (S_{2});\mathbb {Z} )=\mathbb {Z} /10\mathbb {Z} }$ und für den Torus ${\displaystyle H_{1}(\operatorname {Mod} (S_{1});\mathbb {Z} )=\mathbb {Z} /12\mathbb {Z} }$.

Die zweite Gruppenhomologie wurde von Harer berechnet, für ${\displaystyle g\geq 4}$ hat man ${\displaystyle H_{2}(\operatorname {Mod} (S_{g});\mathbb {Z} )=\mathbb {Z} }$.

Die Abbildungsklassengruppen sind residuell endlich.

Kurven auf Flächen

Seien ${\displaystyle \alpha ,\beta }$ einfache geschlossene Kurven auf einer zusammenhängenden Fläche ${\displaystyle S}$. Wir bezeichnen mit ${\displaystyle S_{\alpha },S_{\beta }}$ die durch Aufschneiden entlang ${\displaystyle \alpha }$ bzw. ${\displaystyle \beta }$ aus ${\displaystyle S}$ entstehenden Flächen. Wir sagen, dass ${\displaystyle \alpha }$ eine separierende bzw. nicht separierende Kurve ist wenn ${\displaystyle S_{\alpha }}$ unzusammenhängend bzw. zusammenhängend ist.

Die folgende Eigenschaft wird als change of coordinates principle für die Wirkung der Abbildungsklassengruppe bezeichnet:

Es gibt einen Homöomorphismus ${\displaystyle \phi \colon S\to S}$ mit ${\displaystyle \phi (\alpha )=\beta }$ dann und nur dann, wenn

• entweder ${\displaystyle \alpha }$ und ${\displaystyle \beta }$ beide nicht-separierende Kurven sind,
• oder beide separierende Kurven sind und die (unzusammenhängenden) Flächen ${\displaystyle S_{\alpha }}$ und ${\displaystyle S_{\beta }}$ zueinander homöomorph sind.

Ein wichtiges Hilfsmittel beim Studium der Abbildungsklassengruppe ist der Kurvenkomplex.

Satz von Dehn-Nielsen-Baer

Die Abbildungsklassengruppe ${\displaystyle \operatorname {Mod} (S)}$ ist eine Untergruppe vom Index 2 in der „erweiterten Abbildungsklassengruppe“ ${\displaystyle Mod^{\pm }(S)}$ der Isotopieklassen aller (nicht-notwendig orientierungserhaltender) Homöomorphismen.

Der Satz von Dehn-Nielsen-Baer (benannt nach Max Dehn, Jakob Nielsen und Reinhold Baer) besagt, dass es einen Isomorphismus

${\displaystyle \operatorname {Mod} ^{\pm }(S)=\operatorname {Out} (\pi _{1}S)}$

gibt, wobei ${\displaystyle \pi _{1}S}$ die Fundamentalgruppe der Fläche ${\displaystyle S}$ und ${\displaystyle \operatorname {Out} (\pi _{1}S):=\operatorname {Aut} (\pi _{1}S)/\operatorname {Inn} (\pi _{1}S)}$ ihre äußere Automorphismengruppe bezeichnet.^[3]

Für jeden asphärischen Raum ${\displaystyle M}$ ist die Gruppe der Selbst-Homotopieäquivalenzen modulo Homotopie isomorph zu ${\displaystyle \operatorname {Out} (\pi _{1}M)}$. Aus dem Satz von Dehn-Nielsen-Baer folgt also, dass man die Abbildungsklassengruppe äquivalent auch als Gruppe der Selbst-Homotopieäquivalenzen (statt nur der Homöomorphismen) modulo Homotopie definieren könnte.

Torelli-Gruppe

Die Wirkung von ${\displaystyle \operatorname {Mod} (S_{g})}$ auf ${\displaystyle H_{1}(S_{g};\mathbb {R} )}$ erhält die Schnittform, welche eine symplektische Form ist. Man erhält dadurch einen surjektiven Homomorphismus

${\displaystyle \operatorname {Mod} (S_{g})\to \operatorname {Sp} (2g;\mathbb {Z} )}$,

dessen Kern als Torelli-Gruppe bezeichnet wird.

Satz von Johnson: Für ${\displaystyle g\geq 3}$ wird die Torelli-Gruppe erzeugt von ${\displaystyle \tau _{\alpha }\tau _{\beta }^{-1}}$ für Paare ${\displaystyle (\alpha ,\beta )}$, die einen 2-fach punktierten Torus beranden.^[4]

Alle 3-dimensionalen Homologiesphären lassen sich durch Heegaard-Zerlegungen gewinnen, deren Verklebeabbildung ein Element der Torelli-Gruppe repräsentiert.

Flächen mit markierten Punkten

Für eine geschlossene, orientierbare Fläche ${\displaystyle S}$ vom Geschlecht ${\displaystyle g}$ mit ${\displaystyle r}$ Punkten ${\displaystyle x_{1},\ldots ,x_{r}\in S}$ definiert man

${\displaystyle \Gamma _{g,r}=\operatorname {Mod} (S_{g,r})}$

als die Gruppe der Homotopieklassen von Homöomorphismen ${\displaystyle \phi \colon S\to S}$ mit ${\displaystyle \phi (x_{1})=x_{1},\ldots ,\phi (x_{r})=x_{r}}$, wobei auch die Homotopien die Punkte ${\displaystyle x_{1},\ldots ,x_{r}}$ festlassen sollen.

Die Abbildungsklassengruppen ${\displaystyle \Gamma _{g,r}}$ für unterschiedliche ${\displaystyle r}$ hängen über Birman-Sequenzen miteinander zusammen.

In verschiedenen Zusammenhängen ist es einfacher, ${\displaystyle \Gamma _{g,1}}$ statt ${\displaystyle \Gamma _{g,0}}$ zu untersuchen, etwa bei der Berechnung der stabilen Homologie von Abbildungsklassengruppen (Satz von Madsen-Weiss).

Literatur

• Benson Farb, Dan Margalit: A primer on mapping class groups. (= Princeton Mathematical Series. 49). Princeton University Press, Princeton, NJ 2012, ISBN 978-0-691-14794-9. (online; pdf)
• Nikolai Ivanov: Mapping class groups. In: R. J. Daverman (Hrsg.): Handbook of geometric topology. North-Holland, Amsterdam 2002, ISBN 0-444-82432-4, S. 523–633.

Weblinks

• Yair Minsky: A brief introduction to mapping class groups.
• Gwenaël Massuyeau: A short introduction to mapping class groups.

Einzelnachweise

1. ↑ Für Flächen kann man die Abbildungsklassengruppe äquivalent auch durch Isotopieklassen von Diffeomorphismen definieren: ${\displaystyle \operatorname {Mod} (S):=\pi _{0}(Diff^{+}(S,\partial S))}$. Weiterhin besagt ein Satz von Baer, dass Homöomorphismen von Flächen genau dann isotop sind, wenn sie homotop sind, weshalb man die Abbildungsklassengruppe von Flächen auch durch Homotopieklassen von Homöomorphismen definieren könnte. Das gilt entsprechend auch für Flächen mit Rand, wo zwei den Rand punktweise festlassende Homöomorphismen genau dann isotop sind, wenn sie homotop sind (bzgl. den Rand punktweise festlassender Isotopien bzw. Homotopien).
2. ↑ Alle Beispiele in diesem Abschnitt finden sich in Kapitel 2 von Farb-Margalit (op.cit.).
3. ↑ H. Zieschang, E. Vogt, H.-D. Coldewey: Flächen und ebene diskontinuierliche Gruppen. (= Lecture Notes in Mathematics. Vol. 122). Springer-Verlag, Berlin/New York 1970, ISBN 3-540-04911-8.
4. ↑ Dennis L. Johnson: Homeomorphisms of a surface which act trivially on homology. In: Proc. Amer. Math. Soc. 75, no. 1, 1979, S. 119–125.