Dodekaeder

Regelmäßiges Pentagondodekaeder
Art der Seitenflächen	regelmäßige Fünfecke
Anzahl der Flächen	12
Anzahl der Ecken	20
Anzahl der Kanten	30
Schläfli-Symbol	{5,3}
dual zu	Ikosaeder
Körpernetz
Anzahl verschiedener Netze	43380
Anzahl Kanten in einer Ecke	3
Anzahl Ecken einer Fläche	5

Das Dodekaeder [ˌdodekaˈʔeːdɐ] (von griech. Zwölfflächner; dt. auch (das) Zwölfflach) ist ein Körper mit zwölf Flächen. In der Regel ist damit ein platonischer Körper gemeint, nämlich das regelmäßige Pentagondodekaeder, ein Körper mit

• 12 kongruenten regelmäßigen Fünfecken
• 30 gleich langen Kanten, von denen jede die Seite von zwei Fünfecken ist
• 20 Ecken, in denen jeweils drei dieser Fünfecke zusammentreffen

Es gibt aber auch andere Dodekaeder von hoher Symmetrie.

Symmetrie

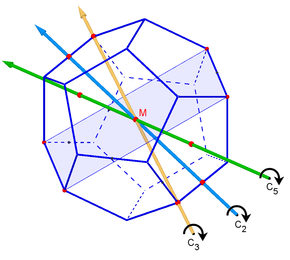
Wegen seiner hohen Symmetrie – alle Ecken, Kanten und Flächen sind untereinander gleichartig – ist das Dodekaeder ein reguläres Polyeder. Es hat:

• 6 fünfzählige Drehachsen ${\displaystyle C_{5}}$ (durch die Mittelpunkte zweier gegenüberliegender Flächen)
• 10 dreizählige Drehachsen ${\displaystyle C_{3}}$ (durch gegenüberliegende Ecken)
• 15 zweizählige Drehachsen ${\displaystyle C_{2}}$ (durch die Mittelpunkte gegenüberliegender Kanten)
• 15 Symmetrieebenen (durch einander gegenüberliegende und parallele Kanten)

und ist

• punktsymmetrisch (Punktspiegelung bezüglich des Dodekaedermittelpunkts)

Insgesamt hat die Symmetriegruppe des Dodekaeders – die Dodekaedergruppe oder Ikosaedergruppe – 120 Elemente. Die 60 orientierungserhaltenden Symmetrien entsprechen der alternierenden Gruppe ${\displaystyle A_{5}}$. Manchmal wird auch diese Untergruppe Ikosaedergruppe genannt. Die volle Symmetriegruppe ist isomorph zu dem direkten Produkt ${\displaystyle A_{5}\times C_{2}}$. Dass das Produkt direkt ist, sieht man daran, dass die Punktspiegelung am Mittelpunkt mit den Drehungen kommutiert.

Die Symmetrie des Dodekaeders ist durch die hier auftretenden fünfzähligen Symmetrieachsen mit einer periodischen Raumstruktur nicht verträglich (siehe Parkettierung). Es kann daher kein Kristallgitter mit Ikosaedersymmetrie geben (siehe Quasikristalle).

Struktur

Das Ikosaeder ist das zum Dodekaeder duale Polyeder und umgekehrt.

Mit Hilfe von Dodekaeder und Ikosaeder können zahlreiche Körper konstruiert werden, die ebenfalls die Dodekaedergruppe als Symmetriegruppe haben. So erhält man zum Beispiel

• das abgestumpfte Dodekaeder mit 12 Zehnecken und 20 Dreiecken durch Abstumpfung der Ecken eines Dodekaeders
• das Ikosidodekaeder mit 12 Fünfecken und 20 Dreiecken
• das abgestumpfte Ikosaeder (Fußballkörper) mit 12 Fünfecken und 20 Sechsecken als Durchschnitt eines Dodekaeders mit einem Ikosaeder (siehe archimedische Körper, Fullerene)
• und das Rhombentriakontaeder mit 12 + 20 = 32 Ecken und 30 Rauten als Flächen. Es entsteht durch das Aufsetzen gerader Pyramiden auf das Dodekaeder, von denen je zwei Seitenflächen einander ergänzen, d. h. in einer Ebene liegen und eine Kante gemein haben.

Aus den Kanten des Dodekaeders kann man 3 Paare gegenüberliegender Kanten so auswählen, dass diese Paare 3 kongruente, zueinander paarweise orthogonale Rechtecke aufspannen. Die restlichen 8 Ecken bilden dann die Ecken eines dem Dodekaeder einbeschriebenen Würfels. Insgesamt gibt es fünf derartige Positionen, wobei jede Kante des Dodekaeders zu genau einer solchen Position gehört und jede Ecke Eckpunkt von zwei einbeschriebenen Würfeln ist. Die Symmetriegruppe des Dodekaeders bewirkt alle 5! = 120 Permutationen dieser fünf Positionen bzw. Würfel.

Da die Kanten des einbeschriebenen Würfels Diagonalen der Fünfecke sind, entspricht das Verhältnis der Längen der Kanten des Dodekaeders und jener eines eingeschriebenen Würfels dem Goldenen Schnitt.

Konstruktion

Euklid beschreibt und beweist im dreizehnten Buch seines Werkes Elemente, unter Proposition 17, die Konstruktion des Dodekaeders.

Um den Aufwand zu minimieren, enthält die folgende sphärischen Darstellung nur die Schritte, die für das Dodekaeder vonnöten sind. Von Vorteil ist hierzu die Anwendung einer sogenannten Dynamische-Geometrie-Software (DGS). Zur besseren Übersicht sind die Kreise und Hilfskugeln zur Erzeugung der Schnittpunkte nur in den betreffenden Bildern der Konstruktion (siehe nebenstehendes Bild der Konstruktionsskizze) bzw. in den animierten Bildern eingezeichnet.

Gegeben sei eine Umkugel, z. B mit dem Radius gleich ${\displaystyle 1}$ und deren Mittelpunkt ${\displaystyle U}$. Beim Bestimmen der ${\displaystyle x-,\;y-}$ und ${\displaystyle z-}$Achsen eines kartesischen Koordinatensystems, entstehen die Punkte ${\displaystyle A_{1},\;B_{1},\;C_{1}}$ und ${\displaystyle D_{1}}$ auf der Oberfläche der Umkugel.

Um ein Dodekaeder darstellen zu können bedarf es hierzu auch der Konstruktion eines Würfels, der ebenfalls von derselben Kugel einbeschrieben ist.^[1][2] Vorab werden aus einem rechtwinkligen Dreieck die beiden Größen Kantenlänge des Würfels und Kantenlänge ${\displaystyle a}$ des Dodekaeders ermittelt.

Auf der verlängerten ${\displaystyle z-}$Achse wird der Punkt ${\displaystyle U'}$ festgelegt und anschließend der Kugeldurchmesser ${\displaystyle |A'_{1}B'_{1}|=2}$ mit Mittelpunkt ${\displaystyle U'}$ auf einer zur ${\displaystyle y-}$Achse Parallelen projiziert. Eine Hilfskugel mit Radius ${\displaystyle |A'_{1}U'|=1}$ markiert ${\displaystyle E_{1}}$ als dritten Punkt für den darauffolgenden Umkreisbogen ${\displaystyle A'_{1}E_{1}B'_{1}}$. Das anschließend eingezeichnete rechtwinklige Dreieck ${\displaystyle D_{2}B'_{1}F_{1}}$ mit der Kathete ${\displaystyle {\overline {B'_{1}D_{2}}}={\tfrac {1}{3}}|A'_{1}B'_{1}|}$ liefert als Hypotenuse ${\displaystyle {\overline {B'_{1}F_{1}}}}$ die Kantenlänge des Würfels. Ihre Teilung im Goldenen Schnitt führt zur Kantenlänge ${\displaystyle a}$ des Dodekaeders.^[3] Zwecks besserer Übersicht wird in diesem Fall die Hypotenuse ${\displaystyle {\overline {B'_{1}F_{1}}}}$ mithilfe eines Kreises um ${\displaystyle B'_{1}}$ mit Richtung parallel zur ${\displaystyle z-}$Achse auf den Durchmesser ${\displaystyle |A'_{1}B'_{1}|}$ übertragen, der Schnittpunkt ist ${\displaystyle G_{1}}$. Nach dem klassischen Verfahren mit innerer Teilung von Heron von Alexandria, folgt die Halbierung der Strecke ${\displaystyle {\overline {B'_{1}G_{1}}}}$ in ${\displaystyle H_{1}}$, das Errichten der Senkrechten in ${\displaystyle G_{1}}$, ein Kreis um ${\displaystyle G_{1}}$ mit Richtung parallel zur ${\displaystyle y-}$Achse (Schnittpunkt ist ${\displaystyle I_{1}}$) und das Einzeichnen des rechtwinkligen Dreiecks ${\displaystyle G_{1}B'_{1}I_{1}}$. Mittels einer ersten Hilfskugel mit Radius ${\displaystyle {\overline {G_{1}I_{1}}}}$ wird die Kathete auf die Hypotenuse ${\displaystyle {\overline {B'_{1}I_{1}}}}$ projiziert, der Schnittpunkt ist ${\displaystyle J_{1}}$. Eine zweite Hilfskugel mit Radius ${\displaystyle {\overline {B'_{1}J_{1}}}}$ erzeugt den Schnittpunkt ${\displaystyle N'}$ auf der Hypotenuse ${\displaystyle {\overline {B'_{1}F_{1}}}}$. Die Länge ${\displaystyle |B'_{1}N'|=a}$ ist der größere Teil der im Goldenen Schnitt geteilten Kantenlänge ${\displaystyle |B'_{1}F_{1}|}$ des Würfels (siehe Bild 4 der Konstruktion). Nach der Halbierung der Kathete ${\displaystyle {\overline {D_{2}F_{1}}}}$ in ${\displaystyle K_{1}}$, der Halbierung der Strecke ${\displaystyle {\overline {B'_{1}N'}}}$ in ${\displaystyle M_{1}}$ und dem Ziehen einer Parallele zu ${\displaystyle {\overline {B'_{1}D_{2}}}}$ mit Schnittpunkt ${\displaystyle M'_{1}}$ liefert die Ähnlichkeit der Dreiecke ${\displaystyle (\triangle {D_{2}B'_{1}F_{1}}\sim \triangle {D_{2}L_{1}K_{1}})}$ den Nachweis: Die Länge ${\displaystyle {\tfrac {1}{2}}a}$ ist der konstruktiv benötigte größere Teil einer im goldenen Schnitt geteilten halben Kante des einbeschriebenen Würfels.^[1]

Die eigentliche Konstruktion des Dodekaeders beginnt mit dem Einzeichnen des Inkreises des Würfels um Mittelpunkt ${\displaystyle U}$ mit Radius ${\displaystyle {\tfrac {1}{2}}|B'_{1}F_{1}|}$ sowie Richtung ${\displaystyle y-}$ und ${\displaystyle z-}$Achse. Die Fertigstellung des Würfels ${\displaystyle ADCBD_{3}FEA_{3}}$, mit den zwölf Punkten aus den Halbierungen der Kanten sowie den acht Mittelpunkten der Quadratflächen, erreicht man mit Parallelen zu den drei Koordinatenachsen, wie z. B. die Kante ${\displaystyle {\overline {AD}}}$ mit der Parallelen zur ${\displaystyle y-}$Achse durch den zuvor ermittelten Kantenmittelpunkt ${\displaystyle L}$ (siehe Bild 6 der Konstruktion).

Weiter geht es mit der Positionierung der regelmäßigen Fünfecke. Bei jedem dieser zwölf Fünfecke liegen zwei seiner gegenüberliegenden Eckpunkte (z. B.: ${\displaystyle B}$ und ${\displaystyle C}$) auf Ecken des Würfels, ein weiterer Eckpunkt (z. B.: ${\displaystyle X}$) hat, so wie die beiden letzten Eckpunkte (z. B.: ${\displaystyle V}$ und ${\displaystyle W}$), den senkrechten Abstand ${\displaystyle {\tfrac {1}{2}}a}$ zu einer Würfelfläche. Die Beschreibung zur Positionierung der Fünfecke erfolgt nun beispielhaft an den beiden Fünfecken ${\displaystyle BXCWV}$ und ${\displaystyle CI_{2}O_{2}FW}$.

Auf der Würfelfläche ${\displaystyle BCFE}$ wird ein Kreis mit Radius ${\displaystyle {\tfrac {1}{2}}a}$ um den Flächenmittelpunkt ${\displaystyle P}$ mit Richtung ${\displaystyle z-}$Achse gezogen. Damit ist die Strecke ${\displaystyle {\overline {NP}}}$ in ${\displaystyle R}$ und die Strecke ${\displaystyle {\overline {PO}}}$ in ${\displaystyle S}$ im Goldenen Schnitt geteilt. Es folgt das Errichten einer Senkrechten zur Würfelfläche in ${\displaystyle S}$. Hierzu zieht man durch ${\displaystyle S}$ eine Parallele zur ${\displaystyle z-}$Achse und den Kreis mit Radius ${\displaystyle {\tfrac {1}{2}}a}$ um ${\displaystyle S}$ mit Richtung parallel zur ${\displaystyle y-}$Achse, der Schnittpunkt ist ${\displaystyle W}$. Eine Parallele zu ${\displaystyle {\overline {NO}}}$ durch ${\displaystyle W}$ und eine Parallele zur ${\displaystyle z-}$Achse durch ${\displaystyle R}$ erzeugen mit ${\displaystyle {\overline {RV}}}$ ebenfalls den Abstand ${\displaystyle {\tfrac {1}{2}}a}$ (siehe Bild 7 der Konstruktion). Nun folgt um den Flächenmittelpunkt ${\displaystyle Q}$, der Würfelfläche ${\displaystyle ADCB}$, ein Kreis mit Radius ${\displaystyle {\tfrac {1}{2}}a}$ mit Richtung parallel zur ${\displaystyle y-}$Achse. Die anschließende Parallele zur ${\displaystyle z-}$Achse durch ${\displaystyle Q}$ schneidet den Kreis in ${\displaystyle T}$. Der nächste Kreis mit Radius ${\displaystyle {\tfrac {1}{2}}a}$ um ${\displaystyle T}$ mit Richtung parallel zur ${\displaystyle y-}$Achse und die Parallele zur ${\displaystyle x-}$Achse durch ${\displaystyle T}$ schneiden sich in ${\displaystyle X}$ (siehe Bild 8 der Konstruktion). Das Fünfeck ${\displaystyle BXCWV}$ wird nun durch Verbinden der soeben bestimmten Eckpunkte fertiggestellt.

Für das Beispiel Fünfeck ${\displaystyle CI_{2}O_{2}FW}$ sind nur noch zwei Eckpunkte zu finden. Um den Flächenmittelpunkt ${\displaystyle K_{2}}$, der Würfelfläche ${\displaystyle DD_{3}FC}$, wird der Kreis mit Radius ${\displaystyle {\tfrac {1}{2}}a}$ um den Flächenmittelpunkt ${\displaystyle K_{2}}$ mit Richtung parallel zur ${\displaystyle z-}$Achse gezogen. Der Schnittpunkt ${\displaystyle F_{2}}$ liegt auf der ${\displaystyle y-}$Achse. Ein zweiter Kreis mit gleichem Radius wird um ${\displaystyle F_{2}}$ mit Richtung ${\displaystyle y-}$Achse eingezeichnet. Die nachfolgende Parallele zur ${\displaystyle x-}$Achse schneidet den Kreis in den Punkten ${\displaystyle I_{2}}$ und ${\displaystyle O_{2}}$ (siehe Bild 13 der Konstruktion). Das Fünfeck ${\displaystyle CI_{2}O_{2}FW}$ wird nun durch Verbinden der betreffenden Eckpunkte fertiggestellt.

Formeln

Die folgende Tabelle ist eine Zusammenstellung von metrischen Eigenschaften eines regulären Dodekaeders, die im nächsten Abschnitt hergeleitet werden.

Größen eines Dodekaeders mit Kantenlänge a
Volumen	${\displaystyle V={\frac {a^{3}}{4}}\left(15+7{\sqrt {5}}\right)\approx 7{,}663\cdot a^{3}}$	ohne Raumwinkel ${\displaystyle \Omega }$ in den Ecken
Oberflächeninhalt	${\displaystyle A_{O}=3{\sqrt {25+10{\sqrt {5}}}}\;a^{2}\;\approx 20{,}646\cdot a^{2}}$
Umkugelradius	${\displaystyle r_{u}={\frac {a}{4}}({\sqrt {5}}+1){\sqrt {3}}\approx 1{,}401\cdot a}$
Kantenkugelradius	${\displaystyle r_{k}={\frac {a}{4}}\left(3+{\sqrt {5}}\right)\approx 1{,}309\cdot a}$
Inkugelradius	${\displaystyle r_{i}={\frac {a}{20}}{\sqrt {250+110{\sqrt {5}}}}\approx 1{,}114\cdot a}$
Verhältnis von Volumen  zu Umkugelvolumen	${\displaystyle {\frac {V}{V_{UK}}}={\frac {\sqrt {15}}{6\pi }}\left(1+{\sqrt {5}}\right)\approx 0{,}665}$
Innenwinkel des regelmäßigen Fünfecks	${\displaystyle \alpha =108^{\circ }}$
Winkel zwischen benachbarten Flächen	${\displaystyle \beta =180^{\circ }-2\arctan \left({\frac {{\sqrt {5}}-1}{2}}\right)\approx 116,56^{\circ }}$
Winkel zwischen Kante und Fläche	${\displaystyle \gamma =90^{\circ }+\arctan \left({\frac {{\sqrt {5}}-1}{2}}\right)\approx 121,72^{\circ }}$
Raumwinkel in den Ecken	${\displaystyle \Omega =2\pi -6\arctan \left({\frac {{\sqrt {5}}-1}{2}}\right)\approx 2{,}962\;\mathrm {sr} }$
Sphärizität	${\displaystyle \Psi ={\frac {\sqrt[{3}]{180\,\pi \left(47+21{\sqrt {5}}\right)}}{6{\sqrt {\left(25+10{\sqrt {5}}\right)}}}}\approx 0{,}91}$

Winkel, Punkte, Flächen, Radien, Koordinaten

Einbeschriebener Würfel

Viele metrische Eigenschaften eines Dodekaeders lassen sich aus der im Bild gezeigten Koordinatendarstellung berechnen/ablesen. In dem Bild wird der Dodekaeder mit der Kantenlänge ${\displaystyle a}$ aus dem Würfel mit der Kantenlänge ${\displaystyle c={\tfrac {{\sqrt {5}}+1}{2}}a}$, der Länge der Diagonale in einer Seitenfläche (5-Eck), aufgebaut. Die Würfelpunkte sind ${\displaystyle (\pm {\tfrac {c}{2}},\pm {\tfrac {c}{2}},\pm {\tfrac {c}{2}})}$. Sie sind 8 der 20 Dodekaeder Punkte. ${\displaystyle P_{1}=({\tfrac {c}{2}},{\tfrac {c}{2}},{\tfrac {c}{2}})}$ ist solch ein Punkt. Beim Rechnen ist immer wieder die Gleichung ${\displaystyle c^{2}=ac+a^{2}}$ nützlich (siehe Goldener Schnitt).

${\displaystyle P_{2}=(0,{\tfrac {a+c}{2}},{\tfrac {a}{2}})}$ ist ein Dodekaederpunkt in der y-z-Ebene.

Um dies einzusehen, muss gezeigt werden, dass der

• Abstand ${\displaystyle d}$ einer nicht in einer Würfelebene liegenden Kante von der Würfelebene gleich ${\displaystyle {\tfrac {a}{2}}}$ ist.

Hierzu wird der Tangens des Winkels ${\displaystyle \varphi }$ (siehe Bild Berechnung v. Winkel) auf zwei Arten ausgedrückt:

${\displaystyle \tan \varphi =d/{\frac {c}{2}}=\left({\frac {c}{2}}-{\frac {a}{2}}\right)/d}$

${\displaystyle \to \ d^{2}={\frac {1}{4}}c(c-a)={\frac {a^{2}}{4}}\ \to \ d={\frac {a}{2}}}$

${\displaystyle \to \ \tan \varphi ={\frac {{\sqrt {5}}-1}{2}}\ \to \ \varphi \approx 31{,}72^{\circ }}$

Winkel

Damit ist (siehe nebenstehendes Bild) der

• Winkel zwischen Seitenflächen ${\displaystyle \ \beta =180^{\circ }-2\varphi \approx 116{,}56^{\circ }}$
• Winkel zwischen einer Kante und einer Seitenfläche ${\displaystyle \ \gamma =90^{\circ }+\varphi \approx 121{,}72^{\circ }}$

Punkte des Dodekaeders

Startet man mit den oben beschriebenen – auch im Bild erkennbaren – Punkten (8 Würfelpunkte, 12 Andere) und will nachweisen, dass sie die Ecken eines regulären Dodekaeders sind, zeigt man, dass

1. alle Punkte auf einer Kugel liegen (Ihr Abstand zum Nullpunkt ist gleich)
2. die Punkte jedes Fünfecks in einer Ebene liegen
3. benachbarte Punkte den Abstand ${\displaystyle a}$ haben.

Unter diesen Bedingungen liegen die Punkte eines jeden Fünfecks auf einem ebenen Schnitt mit der Kugel, also auf einem Kreis, und benachbarte Punkte haben den gleichen Abstand, d. h., das Fünfeck ist regulär.

Um/In/Kanten-Kugelradien

Aus der Zeichnung erkennt man ferner den

• Kantenkugelradius ${\displaystyle \ r_{k}={\frac {a+c}{2}}={\frac {a}{4}}(3+{\sqrt {5}})\approx 1{,}31\;a}$
• Umkugelradius ${\displaystyle \ r_{u}=|OP_{1}|={\frac {c}{2}}{\sqrt {3}}={\frac {a}{4}}({\sqrt {5}}+1){\sqrt {3}}}$

${\displaystyle \qquad \qquad \qquad \quad \;=|OP_{2}|={\frac {a}{4}}{\sqrt {18+6{\sqrt {5}}}}\approx 1{,}40\;a}$

Der Inkugelradius ist (siehe Bild Berechnung v. Winkel) der Abstand der Gerade in der y-z-Ebene durch den Punkt ${\displaystyle (0,r_{k})}$ mit der Steigung ${\displaystyle \tan \varphi }$. Diese Gerade hat die Gleichung

${\displaystyle z={\frac {{\sqrt {5}}-1}{2}}\;y+{\frac {a}{4}}(3+{\sqrt {5}})\ \to \ ({\sqrt {5}}-1)y-2z+{\frac {a}{2}}(3+{\sqrt {5}})=0}$.

Bestimmt man den Abstand dieser Gerade vom Nullpunkt mit Hilfe der Hesseschen Normalform, so ergibt sich der Inkugelradius ${\displaystyle r_{i}}$. Es ist

${\displaystyle r_{i}^{2}={\frac {1}{4}}{\frac {(3+{\sqrt {5}})^{2}}{({\sqrt {5}}-1)^{2}+4}}\;a^{2}={\frac {7+3{\sqrt {5}}}{4(5-{\sqrt {5}})}}\;a^{2}={\frac {50+22{\sqrt {5}}}{80}}\;a^{2}}$

Damit ist der

• Inkugelradius${\displaystyle \ r_{i}={\frac {a}{20}}{\sqrt {250+110{\sqrt {5}}}}\approx 1{,}11\;a}$.

Oberfläche, Volumen

Die Oberfläche des Dodekaeders ist die Summe der 12 der 5-Eckflächen. Die Fläche eines regelmäßigen 5-Ecks ist ${\displaystyle A_{5}={\tfrac {1}{4}}{\sqrt {25+10{\sqrt {5}}}}\;a^{2}\ }$. Damit ist die

• Oberfläche des Dodekaeders: ${\displaystyle \ A_{O}=3{\sqrt {25+10{\sqrt {5}}}}\;a^{2}}$.

Das Volumen des Dodekaeders (Bild 1) ist die Summe des Würfelvolumens und der 6 über jeder Würfelseite liegenden dach-ähnlichen Teile. Das Volumen ${\displaystyle V_{D}}$ eines solchen Dachteiles setzt sich aus dem Volumen einer Pyramide mit Grundfläche ${\displaystyle c(c-a)}$ und Höhe ${\displaystyle {\frac {a}{2}}}$ (siehe Bild) sowie dem dreieckigen Prisma mit Grundfläche ${\displaystyle {\tfrac {1}{2}}c{\tfrac {a}{2}}}$ und Länge ${\displaystyle a}$ zusammen. Also ist

${\displaystyle V_{D}={\frac {1}{3}}c(c-a){\frac {a}{2}}\;+\;{\frac {1}{2}}c{\frac {a}{2}}a={\frac {a^{3}}{24}}(7+3{\sqrt {5}})}$

und es ist das

• Volumen des Dodekaeders: ${\displaystyle \ V=c^{3}+6V_{D}={\frac {a^{3}}{4}}(15+7{\sqrt {5}})\approx 7{,}66\;a^{3}}$

Eine weitere Möglichkeit der Volumenberechnung (Bild 2) ergibt sich, wenn man das Dodekaeder als einen Zusammenbau von 12 gleich großen Pyramiden mit fünfeckiger Grundfläche ansieht. Das Volumen des Dodekaeders entspricht dann dem Volumen von 12 Pyramiden.

Für das Volumen der Pyramide gilt allgemein ${\displaystyle V={\tfrac {1}{3}}Gh}$. Nimmt man für ${\displaystyle G}$ die fünfeckige Grundfläche ${\displaystyle A_{5}={\tfrac {1}{4}}{\sqrt {25+10{\sqrt {5}}}}\;a^{2}\ }$, für ${\displaystyle h}$ die Höhe der Pyramide gleich dem Inkugelradius ${\displaystyle r_{i}={\tfrac {a}{20}}{\sqrt {250+110{\sqrt {5}}}}}$ des Dodekaeders und setzt abschließend den Faktor 12, ergibt sich

${\displaystyle V={\frac {1}{3}}\cdot {\frac {1}{4}}{\sqrt {25+10{\sqrt {5}}}}\;a^{2}\cdot {\frac {a}{20}}{\sqrt {250+110{\sqrt {5}}}}\cdot 12}$

daraus folgt ebenfalls

• Volumen des Dodekaeders: ${\displaystyle \ V={\frac {a^{3}}{4}}(15+7{\sqrt {5}})\approx 7{,}66\;a^{3}}$

Raumwinkel in den Ecken

Der Raumwinkel ${\displaystyle \Omega }$ in einer Dodekaederecke ist der Flächeninhalt des in dem Bild durch rote Punkte markierten sphärischen Dreiecks, das die Kanten einer Ecke auf der Einheitskugel an dieser Ecke ausstechen. Die Winkel dieses sphärischen Dreiecks sind alle gleich dem Winkel ${\displaystyle \beta }$ (siehe oben) zwischen zwei Dreiecksebenen. Der Flächeninhalt des sphärischen Dreiecks ist der Raumwinkel

• ${\displaystyle \Omega =3\beta -\pi =3\left(\pi -2\arctan \left({\frac {{\sqrt {5}}-1}{2}}\right)\right)-\pi }$

${\displaystyle \qquad =2\pi -6\arctan \left({\frac {{\sqrt {5}}-1}{2}}\right)\approx 2{,}961739154\;\mathrm {sr} .}$

Dieser Raumwinkel entspricht der Fläche eines Kugelsegments auf der Einheitskugel mit einem halben Öffnungswinkel ${\displaystyle \theta \approx 58{,}1^{\circ }}$

Anwendungen

• Einige geodätische Kuppeln sind Polyeder, die vom Dodekaeder abgeleitet sind, indem die Fünfecke weiter in gleichschenkelige Dreiecke unterteilt werden.
• Es gibt dodekaederförmige Spielwürfel.
• Dodekaeder werden auch als originelle Wertstoff-Sammelbehälter eingesetzt, zum Beispiel in Paris.
• In der Bauakustik werden dodekaederförmige Lautsprecher verwendet, um eine möglichst gute Kugelcharakteristik zu erhalten.
• Statt einer Glaskugel werden kristallene Zwölfflächner zur Raumausleuchtung verwendet.
• Der Verwendungszweck des römischen Pentagondodekaeders ist bis heute unklar.

• Ein Dodekaeder kann auch als Jahres-Kalender verwendet werden: jeder Monat erhält ein eigenes Fünfeck.
• Sowohl Megaminx als auch Alexander’s Star sind Varianten des Zauberwürfels in Form eines Dodekaeders als dreidimensionales Puzzle.
• In Waldorfschulen ist der Grundstein, der traditionell am Eingangsportal einer jeden Schule platziert wird, ein kupfernes Pentagondodekaeder.^[4][5]

• 
  Ein Dodekaeder als Spielwürfel
• 
  Megaminx, eine Zauberwürfel-Variante
• 
  Ein Dodekaeder als Weihnachtsstern aus der Ausstellung "Sterne – nicht nur zur Weihnachtszeit" im Museum Europäischer Kulturen in Berlin
• 
  Römisches Dodekaeder im Landesmuseum Württemberg, Stuttgart

Pentagondodekaeder mit unregelmäßigen Flächen

Pyritoeder

Das Pyritoeder hat ebenfalls 12 Flächen, 20 Ecken und 30 Kanten. Die Flächen sind aber nicht regelmäßig. Jede der 12 Flächen ist ein Fünfeck mit vier kürzeren und einer längeren Kante. Insgesamt besitzt dieses Polyeder 24 kürzere und 6 längere Kanten.^[6] Wie auch beim regelmäßigen Pentagondodekaeder bilden 8 der 20 Ecken einen einbeschriebenen Würfel (Vergl. Abschnitt 1.3.1); in der Abbildung sind sie gelb markiert. In der Natur kommt Pyrit (FeS₂) manchmal in dieser Gestalt vor. Deshalb wird diese Varietät des Pentagondodekaeder in der Mineralogie auch Pyrit-Dodekaeder oder Pyritoeder^[7] genannt. Bei Kristallen sind fünfzählige Achsen unmöglich, wie das reguläre Pentagondodekaeder sie besitzt, weil es keine lückenlose periodische Flächenfüllung mit fünfzähliger Symmetrie gibt. Nur bei nicht streng periodischen „Kristallen“, also Quasikristallen, ist ein reguläres Pentagondodekaeder denkbar.

Netze des Dodekaeders

Das Dodekaeder hat 43380 Netze.^[8] Das heißt, es gibt 43380 Möglichkeiten, ein hohles Dodekaeder durch Aufschneiden von 19 Kanten aufzuklappen und in der Ebene auszubreiten. Die anderen 11 Kanten verbinden jeweils die 12 regelmäßigen Fünfecke des Netzes. Um ein Dodekaeder so zu färben, dass keine benachbarten Flächen dieselbe Farbe haben, braucht man mindestens 4 Farben.

Graphen, duale Graphen, Zyklen, Färbungen

Das Dodekaeder hat einen ihm zugeordneten ungerichteten planaren Graphen mit 20 Knoten, 30 Kanten und 12 Gebieten, der 3-regulär ist, d. h. von jedem Knoten gehen 3 Kanten aus, sodass der Grad für alle Knoten gleich 3 ist. Bei planaren Graphen ist die genaue geometrische Anordnung der Knoten unwesentlich. Wichtig ist allerdings, dass sich die Kanten nicht schneiden müssen. Die Knoten dieses Dodekaedergraphen entsprechen den Ecken des Dodekaeders.

Die Knoten des Dodekaedergraphen können mit 3 Farben so gefärbt werden, dass benachbarte Knoten immer unterschiedlich gefärbt sind. Dies bedeutet, dass die chromatische Zahl dieses Graphen gleich 3 ist (siehe Knotenfärbung). Außerdem können die Kanten mit 3 Farben so gefärbt werden, dass benachbarte Kanten immer unterschiedlich gefärbt sind. Mit 2 Farben ist das nicht möglich, sodass der chromatische Index für die Kantenfärbung gleich 3 ist (das nebenstehende Bild veranschaulicht diese Färbungen).

Um die entsprechende nötige Anzahl der Farben für die Flächen oder Gebiete zu bestimmen, ist der duale Graph (Ikosaedergraph) mit 12 Knoten, 30 Kanten und 20 Gebieten hilfreich. Die Knoten dieses Graphen werden dabei den Gebieten des Dodekaedergraphen eineindeutig (bijektiv) zugeordnet und umgekehrt (siehe bijektive Funktion und Abbildung). Die Knoten des Ikosaedergraphen können mit 4 Farben so gefärbt werden, dass benachbarte Knoten immer unterschiedlich gefärbt sind, aber nicht mit 3 Farben, sodass die chromatische Zahl des Ikosaedergraphen gleich 4 ist. Daraus lässt sich indirekt schließen: Weil die chromatische Zahl gleich 4 ist, sind 4 Farben für eine solche Flächenfärbung des Dodekaeders oder eine Färbung der Gebiete des Dodekaedergraphen nötig.^[9]

Die 19 aufgeschnittenen Kanten jedes Netzes (siehe oben) bilden zusammen mit den Ecken (Knoten) einen Spannbaum des Dodekaedergraphen. Jedes Netz entspricht genau einem Spannbaum und umgekehrt, sodass hier eine eineindeutige (bijektive) Zuordnung zwischen Netzen und Spannbäumen besteht. Wenn man ein Dodekaedernetz ohne das äußere Gebiet als Graphen betrachtet, erhält man als dualen Graphen jeweils einem Baum mit 12 Knoten und 11 Kanten und dem maximalen Knotengrad 3. Jede Fläche des Dodekaeders wird dabei einem Knoten des Baums zugeordnet. Dabei kommt nicht jede graphentheoretische Konstellation (siehe Isomorphie von Graphen) solcher Bäume vor, aber einige mehrfach.

Der Dodekaedergraph besitzt 60 Hamiltonkreise, aber keine Eulerkreise.^[10]

Andere Dodekaeder

Andere Dodekaeder sind zum Beispiel:

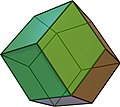
• Das Rhombendodekaeder besitzt 12 kongruente Rauten als Flächen, 14 Ecken und 24 Kanten. Es ist ein catalanischer Körper und dual zum Kuboktaeder. Es bildet die typische Kristallform der Granate.
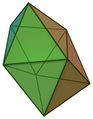
• Das Trigondodekaeder besitzt 12 kongruente gleichseitige Dreiecke als Flächen, 8 Ecken und 18 Kanten. Es ist ein Deltaeder und Johnson-Körper.
• Ausgehöhltes Dodekaeder
• Großes Dodekaeder
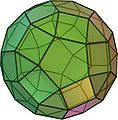
• Rhombenikosidodekaeder
• Verlängertes Rhombendodekaeder

Einige dieser Polyeder haben mehr als 12 Flächen, sind also keine echten Dodekaeder.

• 
  Rhombendodekaeder
• 
  Trigondodekaeder
• 
  Ausgehöhltes Dodekaeder
• 
  Großes Dodekaeder
• 
  Rhombenikosidodekaeder
• 
  Verlängertes Rhombendodekaeder

Weblinks

• Euklid: Stoicheia. Buch XIII.17. Dodekaeder einer Kugel ...
• Herleitung der Formeln
• Bastelbogen für Kalender in Dodekaeder-Form
• Dodekaeder. Mathematische Basteleien
• Dodekaeder-Rechner für Kantenlänge, Oberflächeninhalt, Rauminhalt, Umkugelradius, Kantenkugelradius und Inkugelradius
• Wilfried Stevens: Das Dodekaeder Beitrag im Mystikum-Magazin, Juni 2019

Einzelnachweise

1. ↑ ^{a b c} Euklid, deutsch Rudolf Haller: Stoicheia. Buch XIII.17., S. 20
2. ↑ Euklid, deutsch Rudolf Haller: Stoicheia. Buch XIII.15., S. 15
3. ↑ Euklid, deutsch Rudolf Haller: Stoicheia. Buch XIII.18., S. 24
4. ↑ waldorfschule-muenster.de (Memento vom 11. Juni 2015 im Internet Archive)
5. ↑ siehe z. B. Georg Unger: Das offenbare Geheimnis des Raumes. Meditationen am Pentagondodekaeder nach Carl Kemper. Verlag Freies Geistesleben, Stuttgart 1963.
6. ↑ Dodekaeder / Pentagondodekaeder / Pentagonal dodecahedron. Mineralienatlas, abgerufen am 25. Dezember 2020. 
7. ↑ Nichtsilikate. RUB Fakultät für Geowissenschaften, 2022, abgerufen am 9. Oktober 2022: „Pyrit (FeS2) ist ein messinggelb, metallisch glänzendes und relativ hartes Sulfid, welches gerne in Form von Pentagondodekaedern („Pyritoeder“), Würfel und seltener auch Oktaedern vorkommt (typisch ist außerdem, dass einige Flächen eine Längsstreifung aufweisen können).“ 
8. ↑ Eric Weisstein: Dodecahedron. Netze. In: MathWorld Wolfram. A Wolfram Web Resource, abgerufen am 1. Juli 2020. 
9. ↑ Mike Zabrocki: HOMEWORK #3 SOLUTIONS - MATH 3260. (PDF) York University, Mathematics and Statistics, Toronto, 2003, S. 4, abgerufen am 31. Mai 2020. 
10. ↑ Eric Weisstein: Dodecahedral Graph. Graphen. In: MathWorld Wolfram. A Wolfram Web Resource, abgerufen am 1. Juli 2020.