Koalgebra

Eine Koalgebra ist ein Vektorraum, der die zu einer Algebra duale Struktur besitzt. Das heißt anstelle einer Multiplikation, die zwei Elemente auf ihr Produkt abbildet, gibt es eine Komultiplikation, die ein Element auf ein Tensorprodukt abbildet, und anstelle eines neutralen Elements, das die Einbettung des Grundkörpers in die Algebra ermöglicht, gibt es eine Abbildung aus der Koalgebra in den Grundkörper, die Koeins genannt wird.

Definition

Eine Koalgebra über einem Körper ${\displaystyle k}$ ist ein ${\displaystyle k}$-Vektorraum ${\displaystyle C}$ mit Vektorraumhomomorphismen ${\displaystyle \Delta _{C}\colon C\to C\otimes _{k}C}$, genannt Komultiplikation, Koprodukt oder auch Diagonale, und ${\displaystyle \epsilon _{C}\colon C\to k}$, genannt Koeins, so dass

${\displaystyle (\mathrm {id} _{C}\otimes \Delta _{C})\circ \Delta _{C}=(\Delta _{C}\otimes \mathrm {id} _{C})\circ \Delta _{C}}$ (Koassoziativität)

${\displaystyle (\mathrm {id} _{C}\otimes \epsilon _{C})\circ \Delta _{C}=\mathrm {id} _{C}=(\epsilon _{C}\otimes \mathrm {id} _{C})\circ \Delta _{C}}$ (Koeins)

Ein Koalgebrahomomorphismus zwischen zwei Koalgebren C und D ist ein Vektorraumhomomorphismus ${\displaystyle f\colon C\to D}$ mit

${\displaystyle f\otimes f\circ \Delta _{C}=\Delta _{D}\circ f}$ und ${\displaystyle \epsilon _{C}=\epsilon _{D}\circ f}$.

Beispiel

Sei ${\displaystyle (e_{1},e_{2},e_{3})}$ die kanonische Basis von ${\displaystyle \mathbb {R} ^{3}}$. Man kann auf ${\displaystyle \mathbb {R} ^{3}}$ eine Koalgebra-Struktur mittels

${\displaystyle \Delta _{\mathbb {R} ^{3}}(e_{i})=e_{i}\otimes e_{i}}$

und

${\displaystyle \epsilon _{\mathbb {R} ^{3}}(e_{i})=1}$

definieren.

${\displaystyle \Delta _{\mathbb {R} ^{3}}}$ ist koassoziativ, da

${\displaystyle e_{i}\otimes \Delta _{\mathbb {R} ^{3}}(e_{i})=e_{i}\otimes e_{i}\otimes e_{i}=\Delta _{\mathbb {R} ^{3}}(e_{i})\otimes e_{i}}$,

und ${\displaystyle \epsilon _{\mathbb {R} ^{3}}}$ ist Koeins, da

${\displaystyle e_{i}\otimes \epsilon _{\mathbb {R} ^{3}}(e_{i})=e_{i}=\epsilon _{\mathbb {R} ^{3}}(e_{i})\otimes e_{i}}$.

Die Elemente von ${\displaystyle \mathbb {R} ^{3}\otimes \mathbb {R} ^{3}}$ sind Tensoren zweiter Stufe und können daher als Matrizen dargestellt werden. Die Komultiplikation ist dann

${\displaystyle \Delta _{\mathbb {R} ^{3}}{\begin{pmatrix}a_{1}\\a_{2}\\a_{3}\end{pmatrix}}=a_{1}\Delta _{\mathbb {R} ^{3}}{\begin{pmatrix}1\\0\\0\end{pmatrix}}+a_{2}\Delta _{\mathbb {R} ^{3}}{\begin{pmatrix}0\\1\\0\end{pmatrix}}+a_{3}\Delta _{\mathbb {R} ^{3}}{\begin{pmatrix}0\\0\\1\end{pmatrix}}={\begin{pmatrix}a_{1}&0&0\\0&a_{2}&0\\0&0&a_{3}\end{pmatrix}}}$.

Dualität

Die Multiplikation ${\displaystyle \mu _{A}}$ einer (unitären assoziativen) Algebra ${\displaystyle A}$ ist bilinear, und aufgrund der Universellen Eigenschaft des Tensorprodukts kann sie als Abbildung von ${\displaystyle A\otimes A}$ nach ${\displaystyle A}$ aufgefasst werden. Die Multiplikation ist genau dann assoziativ, wenn das folgende Diagramm kommutiert.

Eine Algebra ${\displaystyle A}$ besitzt genau dann ein neutrales Element, wenn es einen Vektorraumhomomorphismus ${\displaystyle \eta _{A}}$ gibt, so dass das folgende Diagramm kommutiert:

In diesem Fall gilt ${\displaystyle 1_{A}=\eta _{A}(1_{k})}$.

Eine Koalgebra ${\displaystyle C}$ ist eine Algebra in der zu den Vektorräumen ${\displaystyle \mathrm {Vekt} }$ dualen Kategorie ${\displaystyle \mathrm {Vekt} ^{\mathrm {op} }}$. Das heißt, anstelle der Multiplikation gibt es eine Abbildung ${\displaystyle \Delta _{C}\colon C\to C\otimes C}$, so dass das folgende duale Diagramm kommutiert:

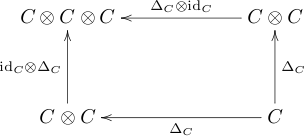
Und anstelle eines neutralen Elements gibt es eine Abbildung ${\displaystyle \epsilon _{C}\colon C\to k}$, so dass das folgende duale Diagramm kommutiert:

Sweedlernotation

Über das Koprodukt ${\displaystyle \Delta _{C}(x)}$ eines Elements ${\displaystyle x\in C}$ ist im Allgemeinen nur bekannt, dass es in ${\displaystyle C\otimes C}$ liegt und sich folglich als

${\displaystyle \Delta _{C}(x)=\sum _{i}x_{(1)}^{(i)}\otimes x_{(2)}^{(i)}}$

darstellen lässt. In der Sweedler-Notation (nach Moss Sweedler) wird dies abgekürzt, indem man symbolisch

${\displaystyle \Delta _{C}(x)=\sum _{(x)}x_{(1)}\otimes x_{(2)}}$

schreibt. In summenloser Sweedler-Notation verzichtet man sogar auf das Summensymbol und schreibt

${\displaystyle \Delta _{C}(x)=x_{(1)}\otimes x_{(2)}}$

Es ist dabei wichtig zu beachten, dass diese Schreibweise nach wie vor eine Summe bezeichnet. Die Symbole ${\displaystyle x_{(1)}}$ und ${\displaystyle x_{(2)}}$ sind für sich allein bedeutungslos und stehen nicht für bestimmte Elemente aus ${\displaystyle C}$, denn die Darstellung von ${\displaystyle \textstyle \Delta _{C}(x)}$ ist nicht eindeutig. Bei Rechnungen in der Sweedlernotation liest man die ${\displaystyle \textstyle x_{(k)}^{(i)}}$ am besten als "geeignete und für diese Rechnung fest gewählte" Elemente.

Diese Schreibweise ermöglicht es, die Komposition von ${\displaystyle \Delta _{C}}$ mit anderen Funktionen als

${\displaystyle (f\otimes g)\circ \Delta _{C}(x)=f(x_{(1)})\otimes g(x_{(2)})}$

zu schreiben.

In summenloser Sweedler-Notation ist ${\displaystyle \epsilon _{C}}$ genau dann Koeins, wenn

${\displaystyle \epsilon _{C}(x_{(1)})x_{(2)}=x=x_{(1)}\epsilon _{C}(x_{(2)})}$.

Das Koprodukt ${\displaystyle \Delta _{C}}$ ist genau dann koassoziativ, wenn

${\displaystyle x_{(1)}\otimes \Delta _{C}(x_{(2)})=\Delta _{C}(x_{(1)})\otimes x_{(2)}}$.

Dieses Element wird in Sweedler-Notation symbolisch als

${\displaystyle \sum _{(x)}x_{(1)}\otimes x_{(2)}\otimes x_{(3)}}$

und summenlos als

${\displaystyle x_{(1)}\otimes x_{(2)}\otimes x_{(3)}}$

geschrieben.

Durch erneutes Anwenden von ${\displaystyle \Delta _{C}}$ entstehen längere Tensorprodukte, die analog geschrieben werden. Dabei muss man die „Indizes“ der hinteren Elemente gegebenenfalls erhöhen:

${\displaystyle f(x_{(1)})\otimes \Delta _{C}(x_{(2)})\otimes g(x_{(3)})=f(x_{(1)})\otimes x_{(2)}\otimes x_{(3)}\otimes g(x_{(4)})}$.

Durch Anwenden von ${\displaystyle \epsilon _{C}}$ verkürzen sich die Tensorprodukte, die „Indizes“ der hinteren Elemente werden entsprechend angepasst:

${\displaystyle f(x_{(1)})\otimes \epsilon _{C}(x_{(2)})\otimes x_{(3)}\otimes g(x_{(4)})=f(x_{(1)})\otimes x_{(2)}\otimes g(x_{(3)})}$.

Literatur

• Christian Kassel: Quantum Groups In: Graduate Texts in Mathematics. Springer-Verlag, ISBN 0-387-94370-6.