Die Feynman-Regeln dienen im Rahmen der störungstheoretisch behandelten Quantenfeldtheorie zur eindeutigen Übersetzung von mathematischen Ausdrücken der Elemente von Streumatrizen in grafische Darstellungen in Form von Feynman-Diagrammen und zurück. Diese Liste der Feynman-Regeln gibt alle Feynman-Regeln des Standardmodells der Teilchenphysik im Impulsraum in den verallgemeinerten Rξ-Eichungen in der gebrochenen Phase wieder.
Die Feynman-Regeln folgen gänzlich aus der Lagrangedichte der betrachteten Quantenfeldtheorie, fundamentalen physikalischen Grundsätzen wie dem Energie- und Impulserhaltungssatz und dem Transformationsverhalten der Teilchen unter den Operationen der Poincaré-Gruppe.
Im Standardmodell kann die Lagrangedichte  in sechs unabhängige Teile aufgespalten werden:
in sechs unabhängige Teile aufgespalten werden:

Struktur der Feynman-Diagramme
→ Hauptartikel: Feynman-Diagramm
Feynman-Diagramme bestehen grundsätzlich aus drei verschiedenen Bausteinen: externen Linien, Propagatoren und Vertices.
Die externen Linien geben die Teilchen an, die im betrachteten Prozess streuen. Es gibt einlaufende Teilchen und auslaufende Teilchen. Nur diese externen Teilchen sind physikalisch beobachtbar. Sie sind asymptotische Zustände; anschaulich gesprochen kommen die Teilchen „aus dem Unendlichen“, wo sie nicht miteinander wechselwirken, und gehen als auslaufende Teilchen nach dem Streuprozess wieder dorthin.
Die Propagatoren beschreiben als interne Linien virtuelle Teilchen, über die die Wechselwirkung zwischen den physikalischen Teilchen vonstatten geht. Diese virtuellen Teilchen sind nicht beobachtbar und verletzen die Energie-Impuls-Relation; sie sind nicht auf der Massenschale.
An den Vertices geschehen die eigentlichen Wechselwirkungen. Dort treffen mehrere Linien aufeinander.
Grundlegende Feynman-Regeln
- Alle externen Teilchen liegen auf der Massenschale. Die LSZ-Reduktionsformel besagt, dass ihnen keine Propagator-Faktoren zugeordnet werden. Zwischen einlaufenden und auslaufenden Teilchen gilt die Energie-Impuls-Erhaltung.
- An allen Vertices gilt die Energie-Impuls-Erhaltung.
- Über alle nicht durch die Energie-Impuls-Erhaltung festgelegten Energien und Impulse wird integriert. Dies tritt auf, wenn im Feynman-Diagramm geschlossene Schleifen von Propagatoren auftreten. Jede solche Schleife führt zu genau einem vierdimensionalen Integral.
- Alle Elemente eines Diagramms werden miteinander multipliziert. Über alle möglichen Diagramme wird summiert.
Externe Teilchen
Die Feynman-Regeln für externe Teilchen folgen aus dem Transformationsverhalten der Teilchen unter der Poincaré-Gruppe. Sie hängen nur von ihrem Spin ab. Gluonen und einige Fermionen, die Quarks, tragen zusätzlich einen Farbindex, da sie an der starken Wechselwirkung teilnehmen und nichttrivial unter den Operationen einer  -Symmetriegruppe des Standardmodells transformieren. Die Spinoren des anderen Typs Fermionen, der Leptonen, tragen keine Farbindices.
-Symmetriegruppe des Standardmodells transformieren. Die Spinoren des anderen Typs Fermionen, der Leptonen, tragen keine Farbindices.
Es existieren keine Feynman-Regeln für externe Faddejew-Popow-Geister, da diese unphysikalisch sind und keine asymptotischen (externen) Zustände bilden können, sondern nur als interne Linien in Feynman-Diagrammen auftreten. Falls Matrixelemente mithilfe der BCFW-Rekursion berechnet werden, führt dies ebenfalls niemals zu Geistern auf externen Linien.[1]
| Typ | Symbol | Beschreibung | Faktor |
Skalarbosonen
Spin 0 |  | einlaufender Skalar |  |
 | auslaufender Skalar |  |
Fermionen
Spin ½ |  | einlaufendes Fermion |  |
 | auslaufendes Fermion |  |
 | einlaufendes Antifermion |  |
 | auslaufendes Antifermion |  |
Eichbosonen
Spin 1 |  | einlaufendes elektroschwaches Boson |  |
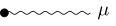 | auslaufendes elektroschwaches Boson |  |
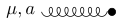 | einlaufendes Gluon |  |
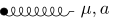 | auslaufendes Gluon |  |
Propagatoren
Die Propagatoren der Teilchen folgen aus der Lagrangedichte. Sie sind die Inversen der kinetischen Terme. Diese kinetischen Terme sind alle Terme, die proportional zum Quadrat der Wellenfunktionen der jeweiligen Felder sind. Für die Eichbosonen und ihre korrespondierenden Goldstone-Bosonen sowie Geister ergibt sich die Besonderheit, dass die Propagatoren von einem Eichparameter abhängen. Dieser muss in der Lagrangedichte in Form von Termen in  eingeführt werden, da die kinetischen Terme der Eichfelder ansonsten nicht invertierbar sind. Diese Eichfixierungsterme enthalten auch Terme proportional zum Quadrat der Goldstone-Bosonen. Da zuletzt noch die Faddejew-Popow-Geister eingeführt werden, um unphysikalische Freiheitsgrade der Eichbosonen zu eliminieren, hängt auch ihr Propagator von der gewählten Eichung ab.
eingeführt werden, da die kinetischen Terme der Eichfelder ansonsten nicht invertierbar sind. Diese Eichfixierungsterme enthalten auch Terme proportional zum Quadrat der Goldstone-Bosonen. Da zuletzt noch die Faddejew-Popow-Geister eingeführt werden, um unphysikalische Freiheitsgrade der Eichbosonen zu eliminieren, hängt auch ihr Propagator von der gewählten Eichung ab.
Die kinetischen Terme lauten:
- für die Eichfelder

- für die Fermionen

- für das Higgs-Boson

- für die Goldstone-Bosonen

- für die Faddejew-Popow-Geister

| Typ | Symbol | Beschreibung | Faktor |
Skalarbosonen
Spin 0 | 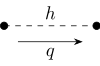 | Higgs-Boson |  |
 | Goldstone-W-Boson |  |
 | Goldstone-Z-Boson |  |
Fermionen
Spin ½ |  | Fermion |  |
Eichbosonen
Spin 1 | 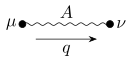 | Photon |  |
 | W-Boson |  |
 | Z-Boson |  |
 | Gluon |  |
Geister
Spin 0 |  | Photon-Geist |  |
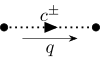 | W-Geist |  |
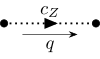 | Z-Geist |  |
 | Gluon-Geist |  |
Vertices
Eichbosonen-Vertices
Die Eichbosonen-Vertices folgen vollständig aus der Eichbosonen-Lagrangedichte. Diese lautet:

Die  sind die Feldstärketensoren der acht Gluonen der
sind die Feldstärketensoren der acht Gluonen der  , die die starke Wechselwirkung vermitteln, der drei W-Bosonen der
, die die starke Wechselwirkung vermitteln, der drei W-Bosonen der  und des einen B-Bosons der
und des einen B-Bosons der  , die nach der elektroschwachen Symmetriebrechung zu den vier Ladungs- und Masseneigenzuständen
, die nach der elektroschwachen Symmetriebrechung zu den vier Ladungs- und Masseneigenzuständen  mischen. Diese Feldstärketensoren sind definiert durch
mischen. Diese Feldstärketensoren sind definiert durch

Neben den kinetischen Termen, die zu den Propagatoren führen, ergibt dies für die starke Wechselwirkung die folgenden beiden Wechselwirkungterme:[2]

Die Feynman-Regeln werden nach einer Symmetrisierung der Terme in den drei bzw. vier Gluonen ersichtlich.[3]
Im Fall der elektroschwachen Vertices sind die Terme nicht in der (elektrischen) Ladungs- und Masseneigenbasis angegeben, sodass die physikalischen Wechselwirkungen nicht offensichtlich sind. Nach der Rotation im Zustandsraum vermittels

ergeben sich die folgenden sechs Terme:[4]
![{\displaystyle {\begin{aligned}{\mathcal {L}}_{\mathrm {W/Z/A} }\supset &-\mathrm {i} gc_{w}\left[\partial ^{\mu }Z^{\nu }(W_{\mu }^{+}W_{\nu }^{-}-W_{\nu }^{+}W_{\mu }^{-})+Z^{\nu }(-W^{\mu +}\partial _{\nu }W_{\mu }^{-}+W^{\mu -}\partial _{\nu }W_{\mu }^{+}+W_{\mu }^{+}\partial ^{\mu }W_{\nu }^{-}-W_{\mu }^{-}\partial _{\mu }W_{\nu }^{+}\right]\\&-\mathrm {i} e\left[\partial ^{\mu }A^{\nu }(W_{\mu }^{+}W_{\nu }^{-}-W_{\nu }^{+}W_{\mu }^{-})+A^{\nu }(-W^{\mu +}\partial _{\nu }W_{\mu }^{-}+W^{\mu -}\partial _{\nu }W_{\mu }^{+}+W_{\mu }^{+}\partial ^{\mu }W_{\nu }^{-}-W_{\mu }^{-}\partial _{\mu }W_{\nu }^{+}\right]\\&-{\frac {g^{2}}{2}}\left[W_{\mu }^{+}W^{\mu -}W_{\nu }^{+}W^{\nu -}-W_{\mu }^{+}W^{\nu -}W_{\mu }^{+}W^{\nu -}\right]\\&+g^{2}c_{w}^{2}\left[Z^{\mu }Z^{\nu }W_{\mu }^{+}W_{\nu }^{-}-Z^{\mu }Z_{\mu }W^{\nu ^{+}}W_{\nu }^{-}\right]\\&+e^{2}\left[A^{\mu }A^{\nu }W_{\mu }^{+}W_{\nu }^{-}-A^{\mu }A_{\mu }W^{\nu ^{+}}W_{\nu }^{-}\right]\\&+egc_{w}\left[A^{\mu }Z^{\nu }W_{\mu }^{+}W_{\nu }^{-}+A^{\mu }Z^{\nu }W_{\nu }^{+}W_{\mu }^{-}-2Z^{\mu }A_{\mu }W^{\nu ^{+}}W_{\nu }^{-}\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3448d20125d7ab8e469365114b41469844109179)
| Typ | Symbol | Beschreibung | Faktor |
| starker Dreier-Vertex |  | 3 Gluonen | ![{\displaystyle {\begin{aligned}g_{s}f^{abc}&\left[g_{\mu \nu }(p-k)_{\rho }\right.\\&+g_{\nu \rho }(k-q)_{\mu }\\&\left.+g_{\rho \mu }(q-p)_{\nu }\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e3a993d0de3f50f2e6f32610972377618b178a4) |
| starker Vierer-Vertex |  | 4 Gluonen | ![{\displaystyle {\begin{aligned}-\mathrm {i} g_{s}^{2}&\left[f^{eab}f^{ecd}(g_{\mu \rho }g_{\nu \sigma }-g_{\mu \sigma }g_{\nu \rho })\right.\\&+f^{eac}f^{edb}(g_{\mu \sigma }g_{\rho \nu }-g_{\mu \nu }g_{\rho \sigma })\\&+\left.f^{ead}f^{ebc}(g_{\mu \nu }g_{\rho \sigma }-g_{\mu \rho }g_{\nu \sigma })\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59523317f1abeef64544ce3311036f40e94b444f) |
| elektroschwacher Dreier-Vertex |  | 2 W-Bosonen
1 Photon | ![{\displaystyle {\begin{aligned}-\mathrm {i} e&\left[g_{\alpha \beta }(p-k)_{\mu }\right.\\&+g_{\beta \mu }(k-q)_{\alpha }\\&\left.+g_{\mu \alpha }(q-p)_{\beta }\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a456b0ec410abbe8a110e952add82e7f83e7b3bc) |
 | 2 W-Bosonen
1 Z-Boson | ![{\displaystyle {\begin{aligned}-\mathrm {i} gc_{w}&\left[g_{\alpha \beta }(p-k)_{\mu }\right.\\&+g_{\beta \mu }(k-q)_{\alpha }\\&\left.+g_{\mu \alpha }(q-p)_{\beta }\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5337c79aba8d033a5889a0450dc35d062575c5ac) |
| elektroschwacher Vierer-Vertex | 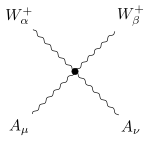 | 2 W-Bosonen
2 Photonen | ![{\displaystyle -\mathrm {i} e^{2}\left[2g_{\alpha \beta }g_{\mu \nu }-g_{\alpha \mu }g_{\beta \nu }-g_{\alpha \nu }g_{\beta \mu }\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5b71f78b1ab1b7a81073c07972d1d1ec37e5e997) |
 | 2 W-Bosonen
2 Z-Bosonen | ![{\displaystyle -\mathrm {i} g^{2}c_{w}^{2}\left[2g_{\alpha \beta }g_{\mu \nu }-g_{\alpha \mu }g_{\beta \nu }-g_{\alpha \nu }g_{\beta \mu }\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b52e468cfe61fdede23bc760ba2ccde1f524f22) |
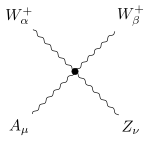 | 2 W-Bosonen
1 Photon
1 Z-Boson | ![{\displaystyle -\mathrm {i} egc_{w}\left[2g_{\alpha \beta }g_{\mu \nu }-g_{\alpha \mu }g_{\beta \nu }-g_{\alpha \nu }g_{\beta \mu }\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b544cc3397a8f0d4af2eed58dcae4a5f026ce0f) |
 | 4 W-Bosonen | ![{\displaystyle \mathrm {i} g^{2}\left[2g_{\alpha \beta }g_{\mu \nu }-g_{\alpha \mu }g_{\beta \nu }-g_{\alpha \nu }g_{\beta \mu }\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/da4943df8b4a62cc3b1271955d08074963d3536b) |
Fermionen-Vertices
Die Lagrangedichte der Fermionen lautet

wobei die Summe über die drei Generationen von Leptonen  und Quarks
und Quarks  läuft. In dieser Formulierung wurden die Anteile linkshändiger und rechtshändiger Chiralität gesondert betrachtet. Sie sind definiert durch Projektion der Wellenfunktionen auf Unterräume mittels der Projektionsoperatoren
läuft. In dieser Formulierung wurden die Anteile linkshändiger und rechtshändiger Chiralität gesondert betrachtet. Sie sind definiert durch Projektion der Wellenfunktionen auf Unterräume mittels der Projektionsoperatoren
 und
und 
Die kovarianten Ableitungen  operieren verschieden je nach Typ und Chiralität des Fermions. Die linkshändigen Fermionen bilden ein Dublett unter der
operieren verschieden je nach Typ und Chiralität des Fermions. Die linkshändigen Fermionen bilden ein Dublett unter der  -Symmetriegruppe, das in der fundamentalen Darstellung transformiert, die rechtshändigen Fermionen ein Singulett, das trivial transformiert. Daher koppeln die drei W-Bosonen der
-Symmetriegruppe, das in der fundamentalen Darstellung transformiert, die rechtshändigen Fermionen ein Singulett, das trivial transformiert. Daher koppeln die drei W-Bosonen der  nur an die linkshändigen Anteile und das B-Boson der
nur an die linkshändigen Anteile und das B-Boson der  an beide Anteile gleichermaßen. Diesen beiden Symmetrien werden die Quantenzahlen schwacher Isospin
an beide Anteile gleichermaßen. Diesen beiden Symmetrien werden die Quantenzahlen schwacher Isospin  und schwache Hyperladung
und schwache Hyperladung  zugeordnet. Im Standardmodell wird diese elektroschwache
zugeordnet. Im Standardmodell wird diese elektroschwache  -Symmetrie spontan zu einer
-Symmetrie spontan zu einer  gebrochen. Die verbleibende Quantenzahl ist die elektrische Ladung. Der Ladungsoperator ist
gebrochen. Die verbleibende Quantenzahl ist die elektrische Ladung. Der Ladungsoperator ist

und operiert auf den Dubletts bzw. Singuletts in der jeweiligen Darstellung.
| | Linkshändig | el. Ladung
 | schw. Isospin
 | schw. Hyperldg.
 | Rechtshändig | el. Ladung
 | schw. Isospin
 | schw. Hyperldg.
 |
| Leptonen |  | 0 | +½ | −1 | – | – | – | – |
 | −1 | −½ | −1 |  | −1 | 0 | −2 |
| Quarks |  | +2/3 | +½ | +1/3 |  | +2/3 | 0 | +4/3 |
 | −1/3 | −½ | +1/3 |  | −1/3 | 0 | −2/3 |
Aus dem Bruch der Symmetrie und dem unterschiedlichen Operationsverhalten ergibt sich, dass die beiden physikalischen geladenen W-Bosonen als Linearkombination aus den drei W-Bosonen ebenfalls nur an die linkshändigen Anteile koppeln. Das physikalische Z-Boson als Linearkombination des W3-Bosons und des B-Bosons der  koppelt mit unterschiedlicher Stärke an links- und rechtshändige Anteile. Das Photon als Eichboson der residualen
koppelt mit unterschiedlicher Stärke an links- und rechtshändige Anteile. Das Photon als Eichboson der residualen  koppelt mit gleicher Stärke an beide Anteile.
koppelt mit gleicher Stärke an beide Anteile.
Für alle linkshändigen Leptonen gilt daher in der Eigenbasis der schwachen Wechselwirkung

und für alle rechtshändigen

Der Faktor  in der Lagrangedichte ist eine Mischungsmatrix, da die Masseneigenzustände der Fermionen nicht mit den Eigenzuständen der schwachen Wechselwirkung übereinstimmen müssen. Dieser Faktor ist nur für die Wechselwirkung mit den W-Bosonen von Belang, da in allen neutralen Strömen, bei denen keine Umwandlung verschiedener Generationen stattfindet, die Summe von der Mischungsmatrix unabhängig wird (GIM-Mechanismus). Im leptonischen Fall im Rahmen des Standardmodells ist
in der Lagrangedichte ist eine Mischungsmatrix, da die Masseneigenzustände der Fermionen nicht mit den Eigenzuständen der schwachen Wechselwirkung übereinstimmen müssen. Dieser Faktor ist nur für die Wechselwirkung mit den W-Bosonen von Belang, da in allen neutralen Strömen, bei denen keine Umwandlung verschiedener Generationen stattfindet, die Summe von der Mischungsmatrix unabhängig wird (GIM-Mechanismus). Im leptonischen Fall im Rahmen des Standardmodells ist  und wurde in der obigen Lagrangedichte bereits eingesetzt.
und wurde in der obigen Lagrangedichte bereits eingesetzt.
In den Feynman-Regeln äußert sich dies darin, dass für die Vertices mit W-Bosonen die linkshändigen Anteile herausprojiziert werden müssen. Dies geschieht mithilfe des Faktors  . Der unterschiedlichen Stärke der Kopplungen des Z-Bosons wird durch eine Linearkombination aus
. Der unterschiedlichen Stärke der Kopplungen des Z-Bosons wird durch eine Linearkombination aus  und
und  Rechnung getragen. Die Anteile berechnen sich durch
Rechnung getragen. Die Anteile berechnen sich durch
 und
und 
wobei sich die Faktoren  auf den schwachen Isospin der linkshändigen Fermionen-Dubletts beziehen.
auf den schwachen Isospin der linkshändigen Fermionen-Dubletts beziehen.
Da die Quarks zusätzlich in der fundamentalen Darstellung der  transformieren, erhält ihre kovariante Ableitung den zustäzlichen Term
transformieren, erhält ihre kovariante Ableitung den zustäzlichen Term

wobei die  als Generatoren der
als Generatoren der  bis auf einen Faktor 2 die Gell-Mann-Matrizen im Farbraum sind. Der Faktor
bis auf einen Faktor 2 die Gell-Mann-Matrizen im Farbraum sind. Der Faktor  ist im Fall der Quarks die Cabibbo-Kobayashi-Maskawa-Matrix (CKM-Matrix), die auf die Quarks des down-Typs operiert. Man beachte, dass in der Lagrangedichte die
ist im Fall der Quarks die Cabibbo-Kobayashi-Maskawa-Matrix (CKM-Matrix), die auf die Quarks des down-Typs operiert. Man beachte, dass in der Lagrangedichte die  -Indices in der Summe implizit sind; daher ist in dieser Darstellung
-Indices in der Summe implizit sind; daher ist in dieser Darstellung
 .
.
| Typ | Symbol | Beschreibung | Faktor |
| starker Vertex | 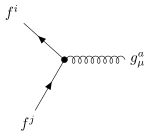 | 2 Fermionen
1 Gluon |  |
| neutrale Ströme |  | 2 Fermionen
1 Photon |  |
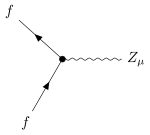 | 2 Fermionen
1 Z-Boson |  |
| geladene Ströme |  | 1 Antifermion des u-Typs
1 Fermion des d-Typs
1 W-Boson |  |
 | 1 Antifermion des d-Typs
1 Fermion des u-Typs
1 W-Boson |  |
Higgs- und Goldstone-Vertices
Die Higgs-Terme in der Lagrangedichte sind die Ursache für die spontane Symmetriebrechung der  und geben den elektroschwachen Eichbosonen ihre Masse. In der ungebrochenen Phase lautet der Anteil
und geben den elektroschwachen Eichbosonen ihre Masse. In der ungebrochenen Phase lautet der Anteil

wobei  ein komplexes Dublett ist, das in der fundamentalen Darstellung der
ein komplexes Dublett ist, das in der fundamentalen Darstellung der  transformiert und
transformiert und  daher dieselbe kovariante Ableitung wie für die linkshändigen Fermionen ist. Die schwache Hyperladung des Dubletts ist
daher dieselbe kovariante Ableitung wie für die linkshändigen Fermionen ist. Die schwache Hyperladung des Dubletts ist  für beiden Einträge. Damit wird der Ladungsoperator zu
für beiden Einträge. Damit wird der Ladungsoperator zu

und das komplexe Dublett kann in Termen von vier reellen Feldern  und dem Vakuumerwartungswert
und dem Vakuumerwartungswert  geschrieben werden:
geschrieben werden:

Nach dem Schreiben in der Masseneigenbasis werden die Terme zu[5]
![{\displaystyle {\begin{aligned}{\mathcal {L}}_{\mathrm {Higgs} }=&\left|\partial _{\mu }\varphi ^{+}+\mathrm {i} \eta g{\frac {c_{w}^{2}-s_{w}^{2}}{2c_{w}}}Z_{\mu }\varphi ^{+}+\mathrm {i} \eta eA_{\mu }\varphi ^{+}+{\frac {1}{2}}\mathrm {i} g\eta W_{\mu }^{+}(v+h+\mathrm {i} \varphi _{Z})\right|^{2}\\&+{\frac {1}{2}}\left|\partial _{\mu }(h+\mathrm {i} \varphi _{Z})+\mathrm {i} \eta gW_{\mu }^{-}\varphi ^{+}-{\frac {1}{2}}\mathrm {i} \eta {\frac {g}{c_{w}}}Z_{\mu }(v+h+\mathrm {i} \varphi _{Z})\right|^{2}\\&-{\frac {1}{2}}m_{h}^{2}h^{2}-{\frac {1}{2}}\lambda vh\left[\varphi ^{+}\varphi ^{-}+{\frac {1}{2}}(\varphi _{Z}^{2}+h^{2})\right]-{\frac {1}{4}}\lambda \left[\varphi ^{+}\varphi ^{-}+{\frac {1}{2}}(\varphi _{Z}^{2}+h^{2})\right]^{2}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/61bf75c6dfa048a3cd3917dddf3c240373ecd61c)
mit der Identifikation  . Die Feynman-Regeln folgen nach der Ausmultiplikation aus allen auftretenden Termen, die drei oder mehr Feldoperatoren beinhalten. Die Parameter
. Die Feynman-Regeln folgen nach der Ausmultiplikation aus allen auftretenden Termen, die drei oder mehr Feldoperatoren beinhalten. Die Parameter  können durch die Relationen
können durch die Relationen
 und
und 
eliminiert werden.
Des Weiteren folgen aus diesem Teil der Lagrangedichte Terme, die bilinear in den Eich- und den Goldstone-Bosonen sind, wie zum Beispiel  . Diese Terme werden durch den Eichfixierungsanteil, der ansonsten keine eigenen Wechselwirkungen erzeugt, vollständig aufgehoben.[6]
. Diese Terme werden durch den Eichfixierungsanteil, der ansonsten keine eigenen Wechselwirkungen erzeugt, vollständig aufgehoben.[6]
| Typ | Symbol | Beschreibung | Faktor |
| Dreier-Vertex mit Eichbosonen |  | 2 Goldstone-W-Bosonen
1 Photon |  |
 | 2 Goldstone-W-Bosonen
1 Z-Boson |  |
 | 1 Higgs-Boson
1 Goldstone-W-Boson
1 W-Boson |  |
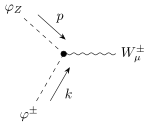 | 1 Goldstone-Z-Boson
1 Goldstone-W-Boson
1 W-Boson |  |
 | 1 Higgs-Boson
1 Goldstone-Z-Boson
Z W-Boson |  |
 | 1 Goldstone-W-Boson
1 W-Boson
1 Photon |  |
 | 1 Goldstone-W-Boson
1 W-Boson
1 Z-Boson |  |
 | 1 Higgs-Boson
2 W-Bosonen |  |
 | 1 Higgs-Boson
2 Z-Bosonen |  |
| Vierer-Vertex mit Eichbosonen |  | 2 Higgs-Bosonen
2 W-Bosonen |  |
 | 2 Goldstone-Z-Bosonen
2 W-Bosonen |  |
 | 2 Higgs-Bosonen
2 Z-Bosonen |  |
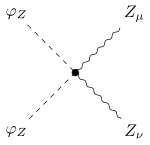 | 2 Goldstone-Z-Bosonen
2 Z-Bosonen |  |
 | 2 Goldstone-W-Bosonen
2 Photonen |  |
 | 2 Higgs-Bosonen
2 Z-Bosonen |  |
 | 2 Goldstone-W-Bosonen
2 W-Bosonen |  |
 | 1 Goldstone-W-Boson
1 Higgs-Boson
1 W-Boson
1 Z-Boson |  |
 | 1 Goldstone-W-Boson
1 Goldstone-Z-Boson
1 W-Boson
1 Z-Boson |  |
 | 1 Goldstone-W-Boson
1 Higgs-Boson
1 W-Boson
1 Photon |  |
 | 1 Goldstone-W-Boson
1 Goldstone-Z-Boson
1 W-Boson
1 Photon |  |
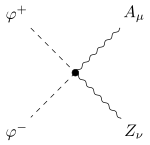 | 2 Goldstone-W-Bosonen
1 Photon
1 Z-Boson |  |
| Dreier-Vertex ohne Eichbosonen |  | 2 Goldstone-W-Bosonen
1 Higgs-Boson |  |
 | 2 Goldstone-Z-Bosonen
1 Higgs-Boson |  |
 | 3 Higgs-Bosonen |  |
| Vierer-Vertex ohne Eichbosonen | 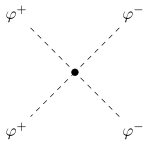 | 4 Goldstone-W-Bosonen |  |
 | 2 Goldstone-W-Bosonen
2 Higgs-Bosonen |  |
 | 2 Goldstone-W-Bosonen
2 Goldstone-Z-Bosonen |  |
 | 4 Higgs-Bosonen |  |
 | 2 Goldstone-Z-Bosonen
2 Higgs-Bosonen |  |
 | 4 Goldstone-Z-Bosonen |  |
Yukawa-Vertices
Der Yukawa-Anteil der Lagrangedichte beschreibt die Kopplung des skalaren Higgs-Feldes an Fermionen. Er lautet:[6]
 .
.
Die  sind dabei die Kopplungskonstanten, die im Fall des Yukawa-Anteils matrixwertig sind und verschiedene Generationen der Fermionen mischen können. Im leptonischen Fall ist dies die Pontecorvo-Maki-Nakagawa-Sakata-Matrix (PMNS-Matrix), im Fall der Quarks die Cabibbo-Kobayashi-Maskawa-Matrix (CKM-Matrix). Die Summe über
sind dabei die Kopplungskonstanten, die im Fall des Yukawa-Anteils matrixwertig sind und verschiedene Generationen der Fermionen mischen können. Im leptonischen Fall ist dies die Pontecorvo-Maki-Nakagawa-Sakata-Matrix (PMNS-Matrix), im Fall der Quarks die Cabibbo-Kobayashi-Maskawa-Matrix (CKM-Matrix). Die Summe über  läuft über die drei Generationen der Fermionen.
läuft über die drei Generationen der Fermionen.  ist die zweite Pauli-Matrix; die Abkürzung
ist die zweite Pauli-Matrix; die Abkürzung  steht für hermitian conjugate und ist so zu verstehen, dass zu den angegebenen Termen die komplex konjugierte Form aller Terme hinzuaddiert werden muss.
steht für hermitian conjugate und ist so zu verstehen, dass zu den angegebenen Termen die komplex konjugierte Form aller Terme hinzuaddiert werden muss.
Nach der spontanen Symmetriebrechung sorgt der Yukawa-Anteil für die Masse der Fermionen im Higgs-Mechanismus und führt zu trilinearen Kopplungen in den Fermionen und den skalaren Higgs- und Goldstone-Bosonen. In der Masseneigenbasis ergeben sich folgende Feynman-Regeln, wobei der Einfachhalt halber in der Darstellung nicht zwischen Leptonen und Quarks unterschieden wird:
| Typ | Symbol | Beschreibung | Faktor |
| neutrale Ströme |  | 2 Fermionen
1 Higgs-Boson |  |
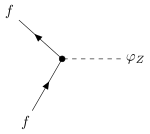 | 2 Fermionen
1 Goldstone-Z-Boson |  |
| geladene Ströme |  | 1 Antifermion des u-Typs
1 Fermion des d-Typs
1 Goldstone-W-Boson |  |
 | 1 Antifermion des d-Typs
1 Fermion des u-Typs
1 Goldstone-W-Boson |  |
Geister-Vertices
Faddejew-Popow-Geister müssen eingeführt werden, um unphysikalische Beiträge aus den Eichfeldern zu kompensieren. Für die Wechselwirkungs-Anteil der Lagrangedichte findet man:[5]
 .
.
Der erste Term beschreibt die Wechselwirkung der starken Geister mit Gluonen, der zweite Terme die der elektroschwachen Geister mit den elektroschwachen Eichbosonen und der letzte Term die der elektroschwachen Geister mit den skalaren Higgs- und Goldstone-Bosonen, wobei der letzte auch die Massenterme der Geister beinhaltet.  ist das Levi-Civita-Symbol als Strukturkonstante der
ist das Levi-Civita-Symbol als Strukturkonstante der  .
.
Nach der Entwicklung in der Masseneigenbasis für den elektroschwachen Anteil folgt für die Lagrangedichte:[5]

| Typ | Symbol | Beschreibung | Faktor |
| starke Geister |  | 1 Gluon-Geist
1 Gluon-Antigeist
1 Gluon |  |
| elektroschwache Geister mit Eichbosonen |  | 1 W-Geist
1 W-Antigeist
1 Photon |  |
 | 1 W-Geist
1 W-Antigeist
1 Z-Boson |  |
 | 1 Z-Geist
1 W-Antigeist
1 W-Boson |  |
 | 1 Photon-Geist
1 W-Antigeist
1 W-Boson |  |
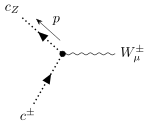 | 1 W-Geist
1 Z-Antigeist
1 W-Boson |  |
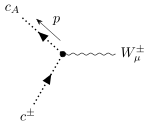 | 1 W-Geist
1 Photon-Antigeist
1 W-Boson |  |
| elektroschwache Geister ohne Eichbosonen | 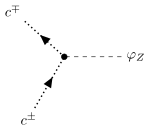 | 1 W-Geist
1 W-Antigeist
1 Goldstone-Z-Boson |  |
 | 1 W-Geist
1 W-Antigeist
1 Higgs-Boson |  |
 | 1 Z-Geist
1 Z-Antigeist
1 Higgs-Boson |  |
 | 1 W-Geist
1 Z-Antigeist
1 Goldstone-W-Boson |  |
 | 1 Z-Geist
1 W-Antigeist
1 Goldstone-Z-Boson |  |
 | 1 Photon-Geist
1 W-Antigeist
1 Goldstone-W-Boson |  |
Einzelnachweise
- ↑ Henriette Elvang und Yu-tin Huang: Scattering Amplitudes in Gauge Theory and Gravity. Cambridge University Press, Cambridge 2015, ISBN 978-1-107-06925-1, S. 125.
- ↑ Mattew D. Schwartz: Quantum Field Theory and the Standard Model. 1. Auflage. Cambridge University Press, Cambridge 2014, ISBN 978-1-107-03473-0, S. 509–511 (englisch).
- ↑ David Bailin und Alexander Love: Introduction to Gauge Field Theory. 2. Auflage. IOP, Bristol und Philadelphia 1993, ISBN 0-7503-0281-X, S. 125–129 (englisch).
- ↑ Mattew D. Schwartz: Quantum Field Theory and the Standard Model. 1. Auflage. Cambridge University Press, Cambridge 2014, ISBN 978-1-107-03473-0, S. 584–588 (englisch).
- ↑ a b c David Bailin und Alexander Love: Introduction to Gauge Field Theory. 2. Auflage. IOP, Bristol und Philadelphia 1993, ISBN 0-7503-0281-X, S. 235–248 (englisch).
- ↑ a b Stefan Pokorski: Gauge Field Theories. 2. Auflage. Cambridge University Press, Cambridge 2000, ISBN 0-521-47816-2, S. 369–373 (englisch).







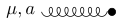
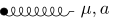













































































































![{\displaystyle {\begin{aligned}{\mathcal {L}}_{\mathrm {W/Z/A} }\supset &-\mathrm {i} gc_{w}\left[\partial ^{\mu }Z^{\nu }(W_{\mu }^{+}W_{\nu }^{-}-W_{\nu }^{+}W_{\mu }^{-})+Z^{\nu }(-W^{\mu +}\partial _{\nu }W_{\mu }^{-}+W^{\mu -}\partial _{\nu }W_{\mu }^{+}+W_{\mu }^{+}\partial ^{\mu }W_{\nu }^{-}-W_{\mu }^{-}\partial _{\mu }W_{\nu }^{+}\right]\\&-\mathrm {i} e\left[\partial ^{\mu }A^{\nu }(W_{\mu }^{+}W_{\nu }^{-}-W_{\nu }^{+}W_{\mu }^{-})+A^{\nu }(-W^{\mu +}\partial _{\nu }W_{\mu }^{-}+W^{\mu -}\partial _{\nu }W_{\mu }^{+}+W_{\mu }^{+}\partial ^{\mu }W_{\nu }^{-}-W_{\mu }^{-}\partial _{\mu }W_{\nu }^{+}\right]\\&-{\frac {g^{2}}{2}}\left[W_{\mu }^{+}W^{\mu -}W_{\nu }^{+}W^{\nu -}-W_{\mu }^{+}W^{\nu -}W_{\mu }^{+}W^{\nu -}\right]\\&+g^{2}c_{w}^{2}\left[Z^{\mu }Z^{\nu }W_{\mu }^{+}W_{\nu }^{-}-Z^{\mu }Z_{\mu }W^{\nu ^{+}}W_{\nu }^{-}\right]\\&+e^{2}\left[A^{\mu }A^{\nu }W_{\mu }^{+}W_{\nu }^{-}-A^{\mu }A_{\mu }W^{\nu ^{+}}W_{\nu }^{-}\right]\\&+egc_{w}\left[A^{\mu }Z^{\nu }W_{\mu }^{+}W_{\nu }^{-}+A^{\mu }Z^{\nu }W_{\nu }^{+}W_{\mu }^{-}-2Z^{\mu }A_{\mu }W^{\nu ^{+}}W_{\nu }^{-}\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3448d20125d7ab8e469365114b41469844109179)
![{\displaystyle {\begin{aligned}g_{s}f^{abc}&\left[g_{\mu \nu }(p-k)_{\rho }\right.\\&+g_{\nu \rho }(k-q)_{\mu }\\&\left.+g_{\rho \mu }(q-p)_{\nu }\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e3a993d0de3f50f2e6f32610972377618b178a4)
![{\displaystyle {\begin{aligned}-\mathrm {i} g_{s}^{2}&\left[f^{eab}f^{ecd}(g_{\mu \rho }g_{\nu \sigma }-g_{\mu \sigma }g_{\nu \rho })\right.\\&+f^{eac}f^{edb}(g_{\mu \sigma }g_{\rho \nu }-g_{\mu \nu }g_{\rho \sigma })\\&+\left.f^{ead}f^{ebc}(g_{\mu \nu }g_{\rho \sigma }-g_{\mu \rho }g_{\nu \sigma })\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59523317f1abeef64544ce3311036f40e94b444f)
![{\displaystyle {\begin{aligned}-\mathrm {i} e&\left[g_{\alpha \beta }(p-k)_{\mu }\right.\\&+g_{\beta \mu }(k-q)_{\alpha }\\&\left.+g_{\mu \alpha }(q-p)_{\beta }\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a456b0ec410abbe8a110e952add82e7f83e7b3bc)
![{\displaystyle {\begin{aligned}-\mathrm {i} gc_{w}&\left[g_{\alpha \beta }(p-k)_{\mu }\right.\\&+g_{\beta \mu }(k-q)_{\alpha }\\&\left.+g_{\mu \alpha }(q-p)_{\beta }\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5337c79aba8d033a5889a0450dc35d062575c5ac)
![{\displaystyle -\mathrm {i} e^{2}\left[2g_{\alpha \beta }g_{\mu \nu }-g_{\alpha \mu }g_{\beta \nu }-g_{\alpha \nu }g_{\beta \mu }\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5b71f78b1ab1b7a81073c07972d1d1ec37e5e997)
![{\displaystyle -\mathrm {i} g^{2}c_{w}^{2}\left[2g_{\alpha \beta }g_{\mu \nu }-g_{\alpha \mu }g_{\beta \nu }-g_{\alpha \nu }g_{\beta \mu }\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b52e468cfe61fdede23bc760ba2ccde1f524f22)
![{\displaystyle -\mathrm {i} egc_{w}\left[2g_{\alpha \beta }g_{\mu \nu }-g_{\alpha \mu }g_{\beta \nu }-g_{\alpha \nu }g_{\beta \mu }\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b544cc3397a8f0d4af2eed58dcae4a5f026ce0f)
![{\displaystyle \mathrm {i} g^{2}\left[2g_{\alpha \beta }g_{\mu \nu }-g_{\alpha \mu }g_{\beta \nu }-g_{\alpha \nu }g_{\beta \mu }\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/da4943df8b4a62cc3b1271955d08074963d3536b)














































![{\displaystyle {\begin{aligned}{\mathcal {L}}_{\mathrm {Higgs} }=&\left|\partial _{\mu }\varphi ^{+}+\mathrm {i} \eta g{\frac {c_{w}^{2}-s_{w}^{2}}{2c_{w}}}Z_{\mu }\varphi ^{+}+\mathrm {i} \eta eA_{\mu }\varphi ^{+}+{\frac {1}{2}}\mathrm {i} g\eta W_{\mu }^{+}(v+h+\mathrm {i} \varphi _{Z})\right|^{2}\\&+{\frac {1}{2}}\left|\partial _{\mu }(h+\mathrm {i} \varphi _{Z})+\mathrm {i} \eta gW_{\mu }^{-}\varphi ^{+}-{\frac {1}{2}}\mathrm {i} \eta {\frac {g}{c_{w}}}Z_{\mu }(v+h+\mathrm {i} \varphi _{Z})\right|^{2}\\&-{\frac {1}{2}}m_{h}^{2}h^{2}-{\frac {1}{2}}\lambda vh\left[\varphi ^{+}\varphi ^{-}+{\frac {1}{2}}(\varphi _{Z}^{2}+h^{2})\right]-{\frac {1}{4}}\lambda \left[\varphi ^{+}\varphi ^{-}+{\frac {1}{2}}(\varphi _{Z}^{2}+h^{2})\right]^{2}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/61bf75c6dfa048a3cd3917dddf3c240373ecd61c)





























































