Orthogonale Koordinaten

In der Mathematik sind orthogonale Koordinaten solche, in denen sich die geometrischen Orte, in denen genau eine Koordinate konstant ist (Kurven, Flächen oder Hyperflächen), alle im rechten Winkel treffen.

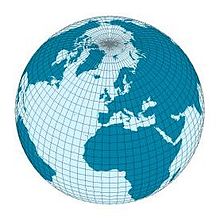
Das Bild zeigt ein auf der Erde weit verbreitetes, krummliniges, aber orthogonales Koordinatensystem, denn die Längen- und Breitenkreise schneiden sich überall rechtwinklig. Auf den dargestellten Längenkreisen ist der Längengrad und auf den Breitenkreisen der Breitengrad konstant. Orthogonale Koordinaten sind ein spezieller, aber häufig benutzter Fall von krummlinigen Koordinaten.

Motivation

Während sich Vektoroperationen und physikalische Gesetze normalerweise am einfachsten in kartesischen Koordinaten ableiten lassen, werden auch nicht-kartesische orthogonale Koordinaten zur Lösung von Problemen verwendet, wenn sie für deren mathematische Beschreibung günstige Eigenschaften haben. Beispielsweise sind die eingangs aufgeführten geographischen Koordinaten gut geeignet für die Navigation auf der Erdoberfläche.

Der Hauptvorteil nichtkartesischer Koordinaten besteht darin, dass sie – wie im genannten Beispiel – so gewählt werden können, dass sie der Geometrie eines betrachteten Problems entsprechen. Auch hängt bei einer weit vom Boden (oder anderen Hindernissen) stattfindenden Explosion die Druckwelle in kartesischen Koordinaten von allen drei Raumdimensionen ab, der Druck bewegt sich jedoch überwiegend vom Zentrum weg, sodass das Problem in sphärischen Koordinaten nahezu eindimensional wird (da die Druckwelle überwiegend nur von der Zeit und dem Abstand vom Zentrum abhängt). Ein weiteres Beispiel ist eine (langsam) fließende Flüssigkeit in einem geraden kreisförmigen Rohr: In kartesischen Koordinaten wäre ein zweidimensionales Randwertproblem zu lösen, während in Zylinderkoordinaten das Problem im Wesentlichen eindimensional wird, siehe Gesetz von Hagen-Poiseuille.

Der Grund dafür, orthogonale Koordinaten anstelle allgemein krummliniger Koordinaten zu bevorzugen, liegt in der Einfachheit: Es treten Komplikationen auf, wenn Koordinaten nicht orthogonal sind. Beispielsweise können in orthogonalen Koordinaten Probleme oft durch die Trennung der Veränderlichen gelöst werden. Die Trennung von Veränderlichen ist eine mathematische Technik, die ein komplexes mehrdimensionales Problem in entsprechend viele eindimensionale Probleme umwandelt, die anhand bekannter Funktionen gelöst werden können. Viele Gleichungen lassen sich auf die Laplace-Gleichung oder die Helmholtz-Gleichung zurückführen. Die Laplace-Gleichung lässt sich in 13 orthogonale Koordinatensysteme auftrennen (die 14 in der Tabelle unten aufgeführten mit Ausnahme von toroidal ), und die Helmholtz-Gleichung lässt sich in 11 orthogonale Koordinatensysteme auftrennen.^[1][2]

Der metrische Tensor hat in orthogonalen Koordinaten Diagonalgestalt, sodass das Skalarprodukt besonders einfache Gestalt annimmt.

Erzeugung orthogonaler Koordinaten

In zwei Dimensionen, wie im Bild, können orthogonale Koordinatensysteme erzeugt werden, indem das Koordinatengitter in der xy-Ebene konform abgebildet wird. Aus den reellen Koordinaten x und y lässt sich eine komplexe Zahl z = x + iy bilden, wobei i die imaginäre Einheit darstellt. Jede holomorphe Funktion w = f( z ) mit komplexer Ableitungsfunktion ungleich null erzeugt eine konforme Abbildung.

Konforme Abbildungen finden Anwendung in der Theorie elektrostatischer Potentiale, der Strömungs- und Technischer Mechanik. Physikalische Systeme, die unveränderlich unter konformen Abbildungen sind, haben eine große Bedeutung in der Festkörperphysik, in der Stringtheorie und in der konformen Feldtheorie.

Orthogonale Koordinaten in drei und höheren Dimensionen können aus einem orthogonalen zweidimensionalen Koordinatensystem erzeugt werden, indem man es entweder in eine neue Dimension projiziert (Zylinderkoordinaten) oder indem man das zweidimensionale System um eine seiner Symmetrieachsen dreht. Allgemeinere orthogonale Koordinaten können konstruiert werden, indem man mit einigen notwendigen Koordinatenflächen beginnt und die mit ihren Normalenvektoren gebildeten Integralkurven berücksichtigt.

Basisvektoren und metrische Faktoren

In kartesischen Koordinaten sind die Vektoren der Standardbasis räumlich konstant, aber in krummlinigen Koordinaten ist dies zumeist nicht der Fall. An jeden Punkt im Raum ist eine Menge von Basisvektoren gebunden, die man sich wie ein begleitendes Dreibein vorstellen kann, das in orthogonalen Koordinaten aus zueinander senkrechten Achsen besteht, schwarz im Bild.

Kovariante Basis

Die kovariante Basis sind die Tangentenvektoren an die Koordinatenlinien im Punkt. Differentialgeometrisch berechnen sich die kovarianten Basisvektoren als Ableitungsfunktion des Ortes nach der (einen) Koordinate ${\displaystyle q^{k}}$:

${\displaystyle {\vec {g}}_{k}={\frac {\partial {\vec {r}}(q^{k})}{\partial q^{k}}}}$

Diese Vektoren haben beliebigen Betrag, sind aber in orthogonalen Systemen paarweise senkrecht zueinander. Die unnormierten Vektoren bilden die natürliche Basis, aus der durch Normierung die normierte Basis entsteht (Einheitsvektoren mit Hut), die in Abgrenzung zu kartesischen Basisvektoren mit einem c bezeichnet werden:^[3]:389

${\displaystyle {\vec {g}}_{k}=\underbrace {\left|{\vec {g}}_{k}\right|} _{\begin{array}{c}{\mathsf {metrischer}}\\[-1ex]{\mathsf {Faktor}}\end{array}}\underbrace {\frac {{\vec {g}}_{k}}{|{\vec {g}}_{k}|}} _{\begin{array}{c}{\mathsf {Einheits-}}\\[-1ex]{\mathsf {vektor}}\end{array}}=h_{k}{\hat {c}}_{k}}$

Kontravariante Basis

Die kontravariante Basis entsteht im Allgemeinen gemäß ${\displaystyle {\vec {g}}^{k}=\operatorname {grad} q^{k}}$ aus dem Gradient der Koordinaten,^[3]:336 sind im Fall orthogonaler Koordinaten jedoch leicht zu finden, weil sie kollinear zu den kovarianten Vektoren sind, aber eine reziproke Länge haben:

${\displaystyle {\vec {g}}^{k}={\frac {{\hat {c}}_{k}}{h_{k}}}={\frac {{\vec {g}}_{k}}{h_{k}^{2}}}}$

Dies folgt aus der Tatsache, dass die ko- und kontravarianten Basisvektoren zueinander reziproke Basis­systeme bilden, mit ${\displaystyle {\vec {g}}_{j}\cdot {\vec {g}}^{k}=\delta _{j}^{k}}$ und dem Kronecker-Delta δ. Zusammengefasst heißt das:

${\displaystyle {\hat {c}}_{k}={\frac {{\vec {g}}_{k}}{h_{k}}}=h_{k}{\vec {g}}^{k}={\hat {c}}^{k}\;,\quad {\hat {c}}_{j}\cdot {\hat {c}}_{k}=\delta _{jk}}$

Metrische Faktoren und Metrikkoeffizienten

Die metrischen Faktoren ${\displaystyle h_{k}=|{\vec {g}}_{k}|={\tfrac {1}{|{\vec {g}}^{k}|}}}$ sind per definitionem positiv und hängen mit den Metrikkoeffizienten^[3]:115 ${\displaystyle g_{jk}:={\vec {g}}_{j}\cdot {\vec {g}}_{k},g^{jk}:={\vec {g}}^{j}\cdot {\vec {g}}^{k}}$ wie folgt zusammen:

${\displaystyle {\begin{aligned}g_{jk}&={\vec {g}}_{j}\cdot {\vec {g}}_{k}=h_{j}{\hat {c}}_{j}\cdot h_{k}{\hat {c}}_{k}=h_{j}h_{k}\delta _{jk}\\g^{jk}&={\vec {g}}^{j}\cdot {\vec {g}}^{k}={\frac {{\hat {c}}_{j}}{h_{j}}}\cdot {\frac {{\hat {c}}_{k}}{h_{k}}}={\frac {\delta _{jk}}{h_{j}h_{k}}}\end{aligned}}}$

Für j≠k verschwinden die Metrikkoeffizienten und für j=k ergibt sich^[3]:390

${\displaystyle h_{k}=|{\vec {g}}_{k}|={\sqrt {g_{kk}}}\;,\quad \left|{\vec {g}}^{k}\right|={\sqrt {g^{kk}}}={\frac {1}{|{\vec {g}}_{k}|}}={\frac {1}{h_{k}}}}$

Koeffizienten von Vektoren

Es gibt demnach drei verschiedenen Basissätze, die zur Beschreibung von Vektoren in orthogonalen Koordinaten üblicherweise verwendet werden: die kovariante Basis ${\displaystyle {\vec {g}}_{k}}$, die kontravariante Basis ${\displaystyle {\vec {g}}^{k}}$ und die normalisierte Basis ${\displaystyle {\hat {c}}_{k}}$, die alle kollinear sind aber verschiedene Längen haben können. Während ein Vektor eine objektive Größe ist, was bedeutet, dass seine Identität unabhängig von einem Koordinatensystem ist, hängen die Koeffizienten eines Vektors davon ab, in welcher Basis der Vektor dargestellt wird. Um Verwirrung zu vermeiden, reflektiert die Stellung des Index das verwendete Basissystem:

${\displaystyle {\vec {x}}=\sum _{k}x^{k}{\vec {g}}_{k}=\sum _{k}x_{k}{\vec {g}}^{k}}$

wo obere Indizes nicht mit Potenzierung verwechselt werden dürfen. Die Position der Indizes gibt an, wie die Koeffizienten berechnet werden:

${\displaystyle x_{k}={\vec {x}}\cdot {\vec {g}}^{k}=h_{k}^{2}x^{k}\;,\quad x^{k}={\vec {x}}\cdot {\vec {g}}_{k}={\frac {x_{k}}{h_{k}^{2}}}}$

Es gibt keine eindeutige, weit verbreitete Notation für Koeffizienten in Bezug auf die normalisierte Basis.

Vektoralgebra

Vektoraddition und -subtraktion erfolgen komponentenweise, genau wie in kartesischen Koordinaten, ohne Komplikationen. Für andere Vektoroperationen können zusätzliche Überlegungen erforderlich sein. Es ist jedoch zu beachten, dass alle Operationen nur für die einem Punkt zugeordneten Vektoren gelten, genauer nur für die Vektoren im Tangentialraum im Punkt definiert sind. Da Basisvektoren im Allgemeinen in orthogonalen Koordinaten von Ort zu Ort variieren, müssen die unterschiedlichen Basisvektoren berücksichtigt werden, wenn zwei Vektoren addiert werden, die an verschiedenen Punkten im Raum vorliegen.

Skalarprodukt

Das Skalarprodukt in einem euklidischen Vektorraum mit kartesischen Koordinaten ist einfach die Summe der Produkte der Koeffizienten. In orthogonalen Koordinaten nimmt das Skalarprodukt zweier Vektoren ${\displaystyle {\vec {x}}}$ und ${\displaystyle {\vec {y}}}$ diese bekannte Form an, wenn die #normalisierte Basis zur Darstellung der Vektoren benutzt wird:

${\displaystyle {\vec {x}}\cdot {\vec {y}}=\sum _{j}x_{j}{\hat {c}}_{j}\cdot \sum _{k}y_{k}{\hat {c}}_{k}=\sum _{j,k}x_{j}x_{k}\delta _{jk}=\sum _{j}x_{j}y_{j}}$

Bezüglich der kovarianten oder kontravarianten Basis ergibt sich mit den #ko- und kontravarianten Koeffizienten:

${\displaystyle {\begin{aligned}{\vec {x}}\cdot {\vec {y}}&=\sum _{j}x_{j}{\vec {g}}^{j}\cdot \sum _{k}y^{k}{\vec {g}}_{k}=\sum _{j,k}x_{j}y^{k}\delta _{k}^{j}\\&=\sum _{k}x_{k}y^{k}=\sum _{k}x^{k}y_{k}=\sum _{k}h_{k}^{2}x^{k}y^{k}=\sum _{k}{\frac {x_{k}y_{k}}{h_{k}^{2}}}\end{aligned}}}$

Kreuzprodukt

Das Kreuzprodukt in kartesischen 3D-Koordinaten lautet:

${\displaystyle {\vec {x}}\times {\vec {y}}=(x_{2}y_{3}-x_{3}y_{2}){\hat {e}}_{1}+(x_{3}y_{1}-x_{1}y_{3}){\hat {e}}_{2}+(x_{1}y_{2}-x_{2}y_{1}){\hat {e}}_{3}}$

Die obige Formel bleibt dann in orthogonalen Koordinaten gültig, wenn sie ein Rechtssystem bilden und die #normalisierte Basis ${\displaystyle {\hat {c}}_{1,2,3}}$ zur Darstellung der Vektoren benutzt wird:

${\displaystyle {\vec {x}}\times {\vec {y}}=(x_{2}y_{3}-x_{3}y_{2}){\hat {c}}_{1}+(x_{3}y_{1}-x_{1}y_{3}){\hat {c}}_{2}+(x_{1}y_{2}-x_{2}y_{1}){\hat {c}}_{3}}$

Mit ihnen gilt wie in kartesischen Koordinaten mit dem Permutationssymbol ϵ:

${\displaystyle {\hat {c}}_{i}\times {\hat {c}}_{j}=\sum _{k=1}^{3}\epsilon _{ijk}{\hat {c}}_{k}}$

Hier kann die #normalisierte Basis mit den ko- und kontravarianten Basisvektoren ausgedrückt werden:

${\displaystyle {\hat {c}}_{k}={\frac {{\vec {g}}_{k}}{h_{k}}}\quad \rightarrow \quad {\vec {g}}_{i}\times {\vec {g}}_{j}=h_{i}h_{j}{\hat {c}}_{i}\times {\hat {c}}_{j}=h_{i}h_{j}\sum _{k=1}^{3}{\frac {\epsilon _{ijk}}{h_{k}}}{\vec {g}}_{k}}$

bzw.

${\displaystyle {\hat {c}}_{k}=h_{k}{\vec {g}}^{k}\quad \rightarrow \quad {\vec {g}}^{i}\times {\vec {g}}^{j}={\frac {{\hat {c}}_{i}\times {\hat {c}}_{j}}{h_{i}h_{j}}}={\frac {1}{h_{i}h_{j}}}\sum _{k=1}^{3}\epsilon _{ijk}h_{k}{\vec {g}}^{k}}$

Dies kann beispielsweise kombiniert werden zu

${\displaystyle {\vec {x}}\times {\vec {y}}=\sum _{i=1}^{3}x^{i}{\vec {g}}_{i}\times \sum _{j=1}^{3}y^{j}{\vec {g}}_{j}=\sum _{i,j,k=1}^{3}x^{i}y^{j}{\frac {h_{i}h_{j}}{h_{k}}}\epsilon _{ijk}{\vec {g}}_{k}}$

was, erweitert geschrieben,

${\displaystyle {\vec {x}}\times {\vec {y}}=\left(x^{2}y^{3}-x^{3}y^{2}\right){\frac {h_{2}h_{3}}{h_{1}}}{\vec {g}}_{1}+\left(x^{3}y^{1}-x^{1}y^{3}\right){\frac {h_{1}h_{3}}{h_{2}}}{\vec {g}}_{2}+\left(x^{1}y^{2}-x^{2}y^{1}\right){\frac {h_{1}h_{2}}{h_{3}}}{\vec {g}}_{3}}$

ergibt.

Vektoranalysis

Nabla-Operator

Der Nabla-Operator lautet in krummlinigen Koordinaten:^[3]:333

${\displaystyle \nabla =\sum _{k}{\vec {g}}^{k}{\frac {\partial }{\partial q^{k}}}=\sum _{k}{\frac {{\vec {c}}_{k}}{h_{k}}}{\frac {\partial }{\partial q^{k}}}}$

Mit ihm können beispielsweise die Differentialoperatoren aus dem Abschnitt #Differentialoperatoren in drei Dimensionen dargestellt werden.

Metrische Faktoren, Weg-, Flächen- und Volumenelemente

Die metrischen Faktoren sind die Beträge der natürlichen Basisvektoren, die sich aus Ableitungsfunktionen des Ortes nach einer Koordinate berechnen:^[3]:279

${\displaystyle {\vec {r}}=\sum _{j}x^{j}{\hat {e}}_{j}\;\rightarrow \quad {\vec {g}}_{k}:={\frac {\partial {\vec {r}}}{\partial q^{k}}}=\sum _{j}{\frac {\partial x^{j}}{\partial q^{k}}}{\hat {e}}_{j}}$

mit Standardbasis ê_1,2,…. Daraus leiten sich die metrischen Faktoren ab:^[3]:391

${\displaystyle h_{k}:={\sqrt {{\vec {g}}_{k}\cdot {\vec {g}}_{k}}}={\sqrt {\sum _{j}\left({\frac {\partial x^{j}}{\partial q^{k}}}\right)^{2}}}}$

Für die Berechnung von Integralen werden gebraucht:^[3]:391f

Wegelement	${\displaystyle \mathrm {d} {\vec {r}}=\sum _{k}h_{k}{\hat {c}}_{k}\mathrm {d} q^{k}}$
Flächenelement	${\displaystyle \mathrm {d} {\vec {a}}^{ij}=h_{i}h_{j}{\hat {c}}_{k}\mathrm {d} q^{i}\mathrm {d} q^{j}}$ mit zyklischen Werten i,j,k
Volumenelement	${\displaystyle \mathrm {d} v=h_{1}h_{2}h_{3}\mathrm {d} q^{1}\mathrm {d} q^{2}\mathrm {d} q^{3}}$

Differentialoperatoren in drei Dimensionen

Die in der Tabelle aufgeführten Operationen kommen in Anwendungen häufig vor.^[3]:403ff

Gradient eines Skalarfeldes	${\displaystyle \operatorname {grad} f=\nabla f={\frac {{\hat {c}}_{1}}{h_{1}}}{\frac {\partial f}{\partial q^{1}}}+{\frac {{\hat {c}}_{2}}{h_{2}}}{\frac {\partial f}{\partial q^{2}}}+{\frac {{\hat {c}}_{3}}{h_{3}}}{\frac {\partial f}{\partial q^{3}}}}$
Divergenz eines Vektorfeldes ${\displaystyle {\vec {f}}=\sum _{k=1}^{3}f_{k}{\hat {c}}_{k}}$:	${\displaystyle {\begin{aligned}\operatorname {div} {\vec {f}}=&\nabla \cdot {\vec {f}}={\frac {1}{h_{1}h_{2}h_{3}}}{\Bigg [}\dots \\&{\frac {\partial }{\partial q^{1}}}(f_{1}h_{2}h_{3})+{\frac {\partial }{\partial q^{2}}}(f_{2}h_{3}h_{1})+{\frac {\partial }{\partial q^{3}}}(f_{3}h_{1}h_{2}){\Bigg ]}\end{aligned}}}$
Rotation eines Vektorfeldes ${\displaystyle {\vec {f}}=\sum _{k=1}^{3}f_{k}{\hat {c}}_{k}}$:	${\displaystyle {\begin{aligned}\nabla \times {\vec {f}}=&{\frac {{\hat {c}}_{1}}{h_{2}h_{3}}}\left[{\frac {\partial }{\partial q^{2}}}(h_{3}f_{3})-{\frac {\partial }{\partial q^{3}}}(h_{2}f_{2})\right]\\&+{\frac {{\hat {c}}_{2}}{h_{3}h_{1}}}\left[{\frac {\partial }{\partial q^{3}}}(h_{1}f_{1})-{\frac {\partial }{\partial q^{1}}}(h_{3}f_{3})\right]\\&+{\frac {{\hat {c}}_{3}}{h_{1}h_{2}}}\left[{\frac {\partial }{\partial q^{1}}}(h_{2}f_{2})-{\frac {\partial }{\partial q^{2}}}(h_{1}f_{1})\right]\end{aligned}}}$
Laplace-Operator eines Skalarfeldes:	${\displaystyle {\begin{aligned}\Delta f=&(\nabla \cdot \nabla )f={\frac {1}{h_{1}h_{2}h_{3}}}{\Bigg [}\dots \\&{\frac {\partial }{\partial q^{1}}}\left({\frac {h_{2}h_{3}}{h_{1}}}{\frac {\partial f}{\partial q^{1}}}\right)+{\frac {\partial }{\partial q^{2}}}\left({\frac {h_{3}h_{1}}{h_{2}}}{\frac {\partial f}{\partial q^{2}}}\right)+{\frac {\partial }{\partial q^{3}}}\left({\frac {h_{1}h_{2}}{h_{3}}}{\frac {\partial f}{\partial q^{3}}}\right){\Bigg ]}\end{aligned}}}$

Bekannte orthogonale Koordinatensysteme

• Zylinderkoordinaten: ${\displaystyle (\rho ,\phi ,z)}$

${\displaystyle \rho \geq 0\,,\quad 0\leq \phi <2\pi \,,\quad -\infty <z<\infty }$

${\displaystyle x=\rho \cos \phi \,,\quad y=\rho \sin \phi \,,\quad z=z}$

• Kugelkoordinaten: ${\displaystyle (r,\theta ,\phi )}$

${\displaystyle r\geq 0\,,\quad 0\leq \theta \leq \pi \,,\quad 0\leq \phi <2\pi }$

${\displaystyle x=r\sin \theta \cos \phi \,,\quad y=r\sin \theta \sin \phi \,,\quad z=r\cos \theta }$

• Parabolische Zylinderkoordinaten: ${\displaystyle (u,v,z)}$

${\displaystyle \quad u\geq 0\,,\quad -\infty <v<\infty \,,\quad -\infty <z<\infty }$

${\displaystyle x=uv\,,\quad y=(u^{2}-v^{2})/2\,,\quad z=z}$

• Parabolische Koordinaten: ${\displaystyle (u,v,\phi )}$

${\displaystyle u\geq 0\,,\quad v\geq 0\,,\quad 0\leq \phi <2\pi }$

${\displaystyle x=uv\cos \phi \,,\quad y=uv\sin \phi \,,\quad z=(u^{2}-v^{2})/2}$

• Elliptische Zylinderkoordinaten: ${\displaystyle (\xi ,\phi ,z)}$

${\displaystyle \xi \geq 0\,,\quad 0\leq \phi <2\pi \,,\quad -\infty <z<\infty }$

${\displaystyle x=a\cosh \xi \cos \phi \,,\quad y=a\sinh \xi \sin \phi \,,\quad z=z}$

• Gestreckte Sphäroid-Koordinaten: ${\displaystyle (\xi ,\theta ,\phi )}$

${\displaystyle \xi \geq 0\,,\quad 0\leq \theta \leq \pi \,,\quad 0\leq \phi <2\pi }$

${\displaystyle x=a\sinh \xi \sin \theta \cos \phi \,,\quad y=a\sinh \xi \sin \theta \sin \phi \,,\quad z=a\cosh \xi \cos \theta }$

• Abgeplattete Sphäroid-Koordinaten: ${\displaystyle (\xi ,\vartheta ,\phi )}$

${\displaystyle \xi \geq 0\,,\quad -\pi /2\leq \vartheta \leq \pi /2\,,\quad 0\leq \phi <2\pi }$

${\displaystyle x=a\cosh \xi \cos \vartheta \cos \phi \,,\quad y=a\cosh \xi \cos \vartheta \sin \phi \,,\quad z=a\sinh \xi \sin \vartheta }$

• Bipolar-Koordinaten: ${\displaystyle (u,v,z)}$

${\displaystyle 0\leq u<2\pi \,,\quad -\infty <v<\infty \,,\quad -\infty <z<\infty }$

${\displaystyle x={\frac {a\sinh v}{\cosh v-\cos u}}\,,\quad y={\frac {a\sin u}{\cosh v-\cos u}}\,,\quad z=z}$

• Ellipsoid-Koordinaten: ${\displaystyle (\lambda ,\mu ,\nu )}$

${\displaystyle {\begin{aligned}{\frac {x^{2}}{a^{2}-\lambda }}+{\frac {y^{2}}{b^{2}-\lambda }}+{\frac {z^{2}}{c^{2}-\lambda }}&=1\ ,\quad \lambda <c^{2}<b^{2}<a^{2}\\{\frac {x^{2}}{a^{2}-\mu }}+{\frac {y^{2}}{b^{2}-\mu }}+{\frac {z^{2}}{c^{2}-\mu }}&=1\ ,\quad c^{2}<\mu <b^{2}<a^{2}\\{\frac {x^{2}}{a^{2}-\nu }}+{\frac {y^{2}}{b^{2}-\nu }}+{\frac {z^{2}}{c^{2}-\nu }}&=1\ ,\quad c^{2}<b^{2}<\nu <a^{2}\end{aligned}}}$

Siehe auch

• Konvektive Koordinaten

Literatur

• G.A. Korn, T. M. Korn: Mathematical Handbook for Scientists and Engineers. Definitions, Theorems, and Formulas for Reference and Review. Dover Publications, 2013, ISBN 978-0-486-32023-6, S. 168–186, doi:10.1002/zamm.19690490921 (eingeschränkte Vorschau in der Google-Buchsuche). 
• P. M. Morse, H. Feshbach: Methods of Theoretical Physics. Band 1. McGraw-Hill, New York 1953, S. 23,115 (archive.org). 
• H. M. Margenau, G. M. Murphy: The Mathematics of Physics and Chemistry. 2. Auflage. Van Nostrand, 1956, ISBN 1-4446-2747-3, S. 168–192 (eingeschränkte Vorschau in der Google-Buchsuche). 
• L. P. Lebedev, M. J. Cloud: Tensor Analysis. World Scientific, 2003, ISBN 981-238-360-3, S. 81–88 (eingeschränkte Vorschau in der Google-Buchsuche). 
• S. Lipschutz, M.R. Spiegel, J. Liu: Mathematical Handbook of Formulas and Tables. McGraw Hill Professional, 2009, ISBN 978-0-07-154855-7, S. 127 f. 

Einzelnachweise

1. ↑ Eric W. Weisstein: Orthogonal Coordinate System. MathWorld, abgerufen am 10. Juli 2008. 
2. ↑ P. M. Morse, H. Feshbach: Methods of Theoretical Physics. Band 1. McGraw-Hill, New York 1953, S. 23,115 (archive.org). 
3. ↑ ^{a b c d e f g h i} Wolfgang Werner: Vektoren und Tensoren als universelle Sprache in Physik und Technik. Tensoralgebra und Tensoranalysis. Band 1. Springer Vieweg Verlag, Wiesbaden 2019, ISBN 978-3-658-25271-7, doi:10.1007/978-3-658-25272-4.