Half-exponential function

In mathematics, a half-exponential function is a functional square root of an exponential function. That is, a function $f$ such that $f$ composed with itself results in an exponential function:^[1]^[2]

f{\bigl (}f(x){\bigr )}=ab^{x},

for some constants

a

and

b

Impossibility of a closed-form formula

If a function $f$ is defined using the standard arithmetic operations, exponentials, logarithms, and real-valued constants, then $f{\bigl (}f(x){\bigr )}$ is either subexponential or superexponential.^[3] Thus, a Hardy L-function cannot be half-exponential.

Construction

Any exponential function can be written as the self-composition $f(f(x))$ for infinitely many possible choices of $f$ . In particular, for every $A$ in the open interval $(0,1)$ and for every continuous strictly increasing function $g$ from $[0,A]$ onto $[A,1]$ , there is an extension of this function to a continuous strictly increasing function $f$ on the real numbers such that $f{\bigl (}f(x){\bigr )}=\exp x$ .^[4] The function $f$ is the unique solution to the functional equation

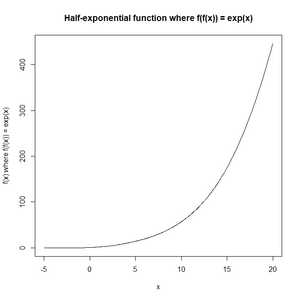
f(x)={\begin{cases}g(x)&{\mbox{if }}x\in [0,A],\\\exp g^{-1}(x)&{\mbox{if }}x\in (A,1],\\\exp f(\ln x)&{\mbox{if }}x\in (1,\infty ),\\\ln f(\exp x)&{\mbox{if }}x\in (-\infty ,0).\\\end{cases}}

A simple example, which leads to $f$ having a continuous first derivative everywhere, is to take $A={\tfrac {1}{2}}$ and $g(x)=x+{\tfrac {1}{2}}$ , giving

f(x)={\begin{cases}\log _{e}\left(e^{x}+{\tfrac {1}{2}}\right)&{\mbox{if }}x\leq -\log _{e}2,\\e^{x}-{\tfrac {1}{2}}&{\mbox{if }}{-\log _{e}2}\leq x\leq 0,\\x+{\tfrac {1}{2}}&{\mbox{if }}0\leq x\leq {\tfrac {1}{2}},\\e^{x-1/2}&{\mbox{if }}{\tfrac {1}{2}}\leq x\leq 1,\\x{\sqrt {e}}&{\mbox{if }}1\leq x\leq {\sqrt {e}},\\e^{x/{\sqrt {e}}}&{\mbox{if }}{\sqrt {e}}\leq x\leq e,\\x^{\sqrt {e}}&{\mbox{if }}e\leq x\leq e^{\sqrt {e}},\\e^{x^{1/{\sqrt {e}}}}&{\mbox{if }}e^{\sqrt {e}}\leq x\leq e^{e},\ldots \\\end{cases}}

Application

Half-exponential functions are used in computational complexity theory for growth rates "intermediate" between polynomial and exponential.^[2] A function $f$ grows at least as quickly as some half-exponential function (its composition with itself grows exponentially) if it is non-decreasing and $f^{-1}(x^{C})=o(\log x)$ , for every $C>0$ .^[5]

References

^ Kneser, H. (1950). "Reelle analytische Lösungen der Gleichung φ(φ(x) = e^x und verwandter Funktionalgleichungen". Journal für die reine und angewandte Mathematik. 187: 56–67. doi:10.1515/crll.1950.187.56. MR 0035385.
^ ^a ^b Miltersen, Peter Bro; Vinodchandran, N. V.; Watanabe, Osamu (1999). "Super-polynomial versus half-exponential circuit size in the exponential hierarchy". In Asano, Takao; Imai, Hiroshi; Lee, D. T.; Nakano, Shin-ichi; Tokuyama, Takeshi (eds.). Computing and Combinatorics, 5th Annual International Conference, COCOON '99, Tokyo, Japan, July 26–28, 1999, Proceedings. Lecture Notes in Computer Science. Vol. 1627. Springer. pp. 210–220. doi:10.1007/3-540-48686-0_21. ISBN 978-3-540-66200-6. MR 1730337.
^ van der Hoeven, J. (2006). Transseries and Real Differential Algebra. Lecture Notes in Mathematics. Vol. 1888. Springer-Verlag, Berlin. doi:10.1007/3-540-35590-1. ISBN 978-3-540-35590-8. MR 2262194. See exercise 4.10, p. 91, according to which every such function has a comparable growth rate to an exponential or logarithmic function iterated an integer number of times, rather than the half-integer that would be required for a half-exponential function.
^ Crone, Lawrence J.; Neuendorffer, Arthur C. (1988). "Functional powers near a fixed point". Journal of Mathematical Analysis and Applications. 132 (2): 520–529. doi:10.1016/0022-247X(88)90080-7. MR 0943525.
^ Razborov, Alexander A.; Rudich, Steven (1997). "Natural proofs". Journal of Computer and System Sciences. 55 (1): 24–35. doi:10.1006/jcss.1997.1494. MR 1473047.