Monotone cubic interpolation

In the mathematical field of numerical analysis, monotone cubic interpolation is a variant of cubic interpolation that preserves monotonicity of the data set being interpolated.

Monotonicity is preserved by linear interpolation but not guaranteed by cubic interpolation.

Monotone cubic Hermite interpolation

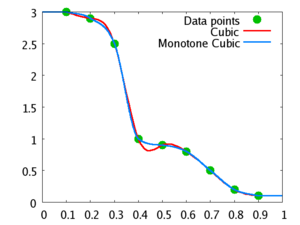
Monotone interpolation can be accomplished using cubic Hermite spline with the tangents ${\displaystyle m_{i}}$ modified to ensure the monotonicity of the resulting Hermite spline.

An algorithm is also available for monotone quintic Hermite interpolation.

Interpolant selection

There are several ways of selecting interpolating tangents for each data point. This section will outline the use of the Fritsch–Carlson method. Note that only one pass of the algorithm is required.

Let the data points be ${\displaystyle (x_{k},y_{k})}$ indexed in sorted order for ${\displaystyle k=1,\,\dots \,n}$.

1. Compute the slopes of the secant lines between successive points:

   ${\displaystyle \delta _{k}={\frac {y_{k+1}-y_{k}}{x_{k+1}-x_{k}}}}$

   for ${\displaystyle k=1,\,\dots \,n-1}$.
   
   
2. These assignments are provisional, and may be superseded in the remaining steps. Initialize the tangents at every interior data point as the average of the secants,

   ${\displaystyle m_{k}={\frac {\delta _{k-1}+\delta _{k}}{2}}}$

   for ${\displaystyle k=2,\,\dots \,n-1}$.
   
   For the endpoints, use one-sided differences:

   ${\displaystyle m_{1}=\delta _{1}\quad {\text{ and }}\quad m_{n}=\delta _{n-1}\,}$.

   If ${\displaystyle \delta _{k-1}}$ and ${\displaystyle \delta _{k}}$ have opposite signs, set ${\displaystyle m_{k}=0}$.
   
   
3. For ${\displaystyle k=1,\,\dots \,n-1}$, where ever ${\displaystyle \delta _{k}=0}$ (where ever two successive ${\displaystyle y_{k}=y_{k+1}}$ are equal),
   set ${\displaystyle m_{k}=m_{k+1}=0,}$ as the spline connecting these points must be flat to preserve monotonicity.
   Ignore steps 4 and 5 for those ${\displaystyle k\,}$.
   
   
4. Let

   ${\displaystyle \alpha _{k}=m_{k}/\delta _{k}\quad {\text{ and }}\quad \beta _{k}=m_{k+1}/\delta _{k}}$.

   If either ${\displaystyle \alpha _{k}}$ or ${\displaystyle \beta _{k}}$ is negative, then the input data points are not strictly monotone, and ${\displaystyle (x_{k},\,y_{k})}$ is a local extremum. In such cases, piecewise monotone curves can still be generated by choosing ${\displaystyle m_{k}=0\,}$ if ${\displaystyle \alpha _{k}<0}$ or ${\displaystyle m_{k+1}=0\,}$ if ${\displaystyle \beta _{k}<0}$, although strict monotonicity is not possible globally.
   
   
5. To prevent overshoot and ensure monotonicity, at least one of the following three conditions must be met:

(a) the function

${\displaystyle \phi _{k}=\alpha _{k}-{\frac {(2\alpha _{k}+\beta _{k}-3)^{2}}{3(\alpha _{k}+\beta _{k}-2)}}>0\,}$, or

(b) ${\displaystyle \alpha _{k}+2\beta _{k}-3\leq 0\,}$, or

(c) ${\displaystyle 2\alpha _{k}+\beta _{k}-3\leq 0\,}$.

Only condition (a) is sufficient to ensure strict monotonicity: ${\displaystyle \phi _{k}}$ must be positive.

One simple way to satisfy this constraint is to restrict the vector ${\displaystyle (\alpha _{k},\,\beta _{k})}$ to a circle of radius 3. That is, if ${\displaystyle \alpha _{k}^{2}+\beta _{k}^{2}>9\,}$, then set

${\displaystyle \tau _{k}={\frac {3}{\sqrt {\alpha _{k}^{2}+\beta _{k}^{2}}}}\,}$,

and rescale the tangents via

${\displaystyle m_{k}=\tau _{k}\,\alpha _{k}\,\delta _{k}\quad {\text{ and }}\quad m_{k+1}=\tau _{k}\,\beta _{k}\,\delta _{k}\,}$.

Alternatively it is sufficient to restrict ${\displaystyle \alpha _{k}\leq 3}$ and ${\displaystyle \beta _{k}\leq 3\,}$. To accomplish this if ${\displaystyle \alpha _{k}>3{\text{ or }}\beta _{k}>3\,}$, then set ${\displaystyle m_{k}=3\,\delta _{k}\,}$.

Cubic interpolation

After the preprocessing above, evaluation of the interpolated spline is equivalent to cubic Hermite spline, using the data ${\displaystyle x_{k}}$, ${\displaystyle y_{k}}$, and ${\displaystyle m_{k}}$ for ${\displaystyle k=1,\,\dots \,n}$.

To evaluate at ${\displaystyle x}$, find the index ${\displaystyle k}$ in the sequence where ${\displaystyle x}$, lies between ${\displaystyle x_{k}}$, and ${\displaystyle x_{k+1}}$, that is: ${\displaystyle x_{k}\leq x\leq x_{k+1}}$. Calculate

${\displaystyle \Delta =x_{k+1}-x_{k}\quad {\text{ and }}\quad t={\frac {x-x_{k}}{\Delta }}}$

then the interpolated value is

${\displaystyle f_{\text{interpolated}}(x)=y_{k}\cdot h_{00}(t)+\Delta \cdot m_{k}\cdot h_{10}(t)+y_{k+1}\cdot h_{01}(t)+\Delta \cdot m_{k+1}\cdot h_{11}(t)}$

where ${\displaystyle h_{ii}}$ are the basis functions for the cubic Hermite spline.

Example implementation

The following JavaScript implementation takes a data set and produces a monotone cubic spline interpolant function:

/*
 * Monotone cubic spline interpolation
 * Usage example listed at bottom; this is a fully-functional package. For
 * example, this can be executed either at sites like
 * https://www.programiz.com/javascript/online-compiler/
 * or using nodeJS.
 */
function DEBUG(s) {
    /* Uncomment the following to enable verbose output of the solver: */
    //console.log(s);
}
var j = 0;
var createInterpolant = function(xs, ys) {
    var i, length = xs.length;
    
    // Deal with length issues
    if (length != ys.length) { throw 'Need an equal count of xs and ys.'; }
    if (length === 0) { return function(x) { return 0; }; }
    if (length === 1) {
        // Impl: Precomputing the result prevents problems if ys is mutated later and allows garbage collection of ys
        // Impl: Unary plus properly converts values to numbers
        var result = +ys[0];
        return function(x) { return result; };
    }
    
    // Rearrange xs and ys so that xs is sorted
    var indexes = [];
    for (i = 0; i < length; i++) { indexes.push(i); }
    indexes.sort(function(a, b) { return xs[a] < xs[b] ? -1 : 1; });
    var oldXs = xs, oldYs = ys;
    // Impl: Creating new arrays also prevents problems if the input arrays are mutated later
    xs = []; ys = [];
    // Impl: Unary plus properly converts values to numbers
    for (i = 0; i < length; i++) { xs.push(+oldXs[indexes[i]]); ys.push(+oldYs[indexes[i]]); }

    DEBUG("debug: xs = [ " + xs + " ]")
    DEBUG("debug: ys = [ " + ys + " ]")
    
    // Get consecutive differences and slopes
    var dys = [], dxs = [], ms = [];
    for (i = 0; i < length - 1; i++) {
        var dx = xs[i + 1] - xs[i], dy = ys[i + 1] - ys[i];
        dxs.push(dx); dys.push(dy); ms.push(dy/dx);
    }
    // Get degree-1 coefficients
    var c1s = [ms[0]];
    for (i = 0; i < dxs.length - 1; i++) {
        var m = ms[i], mNext = ms[i + 1];
        if (m*mNext <= 0) {
            c1s.push(0);
        } else {
            var dx_ = dxs[i], dxNext = dxs[i + 1], common = dx_ + dxNext;
            c1s.push(3*common/((common + dxNext)/m + (common + dx_)/mNext));
        }
    }
    c1s.push(ms[ms.length - 1]);

    DEBUG("debug: dxs = [ " + dxs + " ]")
    DEBUG("debug: ms = [ " + ms + " ]")
    DEBUG("debug: c1s.length = " + c1s.length)
    DEBUG("debug: c1s = [ " + c1s + " ]")
    
    // Get degree-2 and degree-3 coefficients
    var c2s = [], c3s = [];
    for (i = 0; i < c1s.length - 1; i++) {
        var c1 = c1s[i];
        var m_ = ms[i];
        var invDx = 1/dxs[i];
        var common_ = c1 + c1s[i + 1] - m_ - m_;
        DEBUG("debug: " + i + ". c1 = " + c1);
        DEBUG("debug: " + i + ". m_ = " + m_);
        DEBUG("debug: " + i + ". invDx = " + invDx);
        DEBUG("debug: " + i + ". common_ = " + common_);
        c2s.push((m_ - c1 - common_)*invDx);
        c3s.push(common_*invDx*invDx);
    }
    DEBUG("debug: c2s = [ " + c2s + " ]")
    DEBUG("debug: c3s = [ " + c3s + " ]")

    // Return interpolant function
    return function(x) {
        // The rightmost point in the dataset should give an exact result
        var i = xs.length - 1;
        //if (x == xs[i]) { return ys[i]; }
        
        // Search for the interval x is in, returning the corresponding y if x is one of the original xs
        var low = 0, mid, high = c3s.length - 1, rval, dval;
        while (low <= high) {
            mid = Math.floor(0.5*(low + high));
            var xHere = xs[mid];
            if (xHere < x) { low = mid + 1; }
            else if (xHere > x) { high = mid - 1; }
            else {
                j++;
                i = mid;
                var diff = x - xs[i];
                rval = ys[i] + diff * (c1s[i] + diff *  (c2s[i] + diff * c3s[i]));
                dval = c1s[i] + diff * (2*c2s[i] + diff * 3*c3s[i]);
                DEBUG("debug: " + j + ". x = " + x + ". i = " + i + ", diff = " + diff + ", rval = " + rval + ", dval = " + dval);
                return [ rval, dval ];
            }
        }
        i = Math.max(0, high);

        // Interpolate
        var diff = x - xs[i];
        j++;
        rval = ys[i] + diff * (c1s[i] + diff *  (c2s[i] + diff * c3s[i]));
        dval = c1s[i] + diff * (2*c2s[i] + diff * 3*c3s[i]);
        DEBUG("debug: " + j + ". x = " + x + ". i = " + i + ", diff = " + diff + ", rval = " + rval + ", dval = " + dval);
        return [ rval, dval ];
    };
};

/*
   Usage example below will approximate x^2 for 0 <= x <= 4.

   Command line usage example (requires installation of nodejs):
   node monotone-cubic-spline.js
*/

var X = [0, 1, 2, 3, 4];
var F = [0, 1, 4, 9, 16];
var f = createInterpolant(X,F);
var N = X.length;
console.log("# BLOCK 0 :: Data for monotone-cubic-spline.js");
console.log("X" + "\t" + "F");
for (var i = 0; i < N; i += 1) {
    console.log(F[i] + '\t' + X[i]);
}
console.log(" ");
console.log(" ");
console.log("# BLOCK 1 :: Interpolated data for monotone-cubic-spline.js");
console.log("      x       " + "\t\t" + "     P(x)      " + "\t\t" + "    dP(x)/dx     ");
var message = '';
var M = 25;
for (var i = 0; i <= M; i += 1) {
    var x = X[0] + (X[N-1]-X[0])*i/M;
    var rvals = f(x);
    var P = rvals[0];
    var D = rvals[1];
    message += x.toPrecision(15) + '\t' + P.toPrecision(15) + '\t' + D.toPrecision(15) + '\n';
}
console.log(message);

References

• Fritsch, F. N.; Carlson, R. E. (1980). "Monotone Piecewise Cubic Interpolation". SIAM Journal on Numerical Analysis. 17 (2). SIAM: 238–246. doi:10.1137/0717021.
• Dougherty, R.L.; Edelman, A.; Hyman, J.M. (April 1989). "Positivity-, monotonicity-, or convexity-preserving cubic and quintic Hermite interpolation". Mathematics of Computation. 52 (186): 471–494. doi:10.2307/2008477.

External links

• GPLv2 licensed C++ implementation: MonotCubicInterpolator.cpp MonotCubicInterpolator.hpp