Ympyrädiagrammi

Ympyrädiagrammi (myös ympyräkaavio, piirakkakaavio tai sektorikaavio) on diagrammi, jossa ympyrä on jaettu osuuksia kuvaaviin sektoreihin. Nämä ovat tavallisesti suhteellisia osuuksia, jotka on kuvattu prosenttilukuina.[1] Ympyrädiagrammin avulla havainnollistetaan jonkin asian osuuksien suhteita toisiinsa ja kokonaismäärään.
Käyttö

Ympyräkaavio on suosittu kuvaaja etenkin yritysmaailmassa ja tiedotusvälineissä. Ympyräkaaviota suositaan etenkin siksi, koska se on miellyttävän näköinen.[1][2] Ympyräkaavio soveltuu myös erityisen hyvin hahmottamaan osuuksien suhdetta kokonaismäärästä. Tämä johtuu osittain siitä, että lukija pystyy hahmottamaan ympyrän puolikkaan tai neljänneksen ja vertaamaan osion kokoa niihin. Myös yhdistettyjen vierekkäisten osioiden vertailuja toisiin yhdistettyihin osioihin on helpompi tehdä ympyräkaaviosta kuin esimerkiksi yksittäisistä pylväistä koostuvasta pylväskaaviosta.[3]
Ympyräkaavio on kuitenkin verrattain harvinainen tieteellisissä tai teknisissä julkaisuissa. Tämä selittyy osin sillä, että ympyräkaavio havainnollistaa huonosti osuuksien välisiä eroja, jonka vuoksi monet tilastotieteilijät suosittelevat sen käytön välttämistä kokonaan.[3][4]
Ympyräkaavion keksi brittiläinen William Playfair, joka käytti sitä ensimmäistä kertaa vuonna 1801.[5]
Ominaisuudet
Ympyräkaavion sektorin pinta-ala on suhteessa sen esittämään prosenttiosuuteen. Sektoreiden enimmäismääräksi suositellaan kuutta, jotta kaaviosta ei tulisi liian sekavaa. Sektorit järjestetään yleensä suuruusjärjestykseen aloittaen joko kello kolmesta vastapäivään tai kello 12:sta myötäpäivään. Kello kolmesta aloittamisen etuna on se, että siinä kaikkein pienin sektori ei saa korostetun näkyvää asemaa kaavion huipulla. Selittävät tekstit kirjoitetaan yleensä sektoreiden viereen. Koska ympyräkaavio on melko epätarkka, luvut ilmaistaan usein kaaviossa tai selitteiden vieressä.[1][6] Prosenttiosuuksien numeraalinen ilmoittaminen on kuitenkin usein oire siitä, että tekijä ei pidä kaaviota yksinään riittävän havainnollisena.[7]
Kaaviossa voi joskus korostaa tiettyä sektoria leikkaamalla se irti. Pienestä sektorista voi tehdä kaavion viereen myös oman ympyräkaavionsa.[8] Kun ympyräkaavioita käytetään karttadiagrammissa, ympyröiden eri koolla voi esittää kokonaismäärien eroja.[9]
Muunnoksia
Rinkiläkaaviossa keskellä on reikä. Sitä käytetään lähinnä vaihtelun vuoksi, eikä se paranna kaavion selkeyttä. Kerroskaaviossa on sisäkkäisiä ympyräkaavioita, joiden tavoitteena on parantaa kahden ympyräkaavion vertailtavuutta.[10]
Esimerkkejä
-
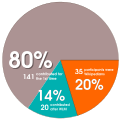 Kello kolmesta vastapäivään luettava ympyrädiagrammi.
Kello kolmesta vastapäivään luettava ympyrädiagrammi. -
 Rinkiläkaavio.
Rinkiläkaavio. -
 Kerrosympyräkaavio, jonka sisäympyrässä ovat Espanjan parlamenttivaalien 2011 äänijakaumat puolueittain ja ulkoympyrässä samojen puolueiden saamat parlamenttipaikat.
Kerrosympyräkaavio, jonka sisäympyrässä ovat Espanjan parlamenttivaalien 2011 äänijakaumat puolueittain ja ulkoympyrässä samojen puolueiden saamat parlamenttipaikat. -
 Ympyrädiagrammi, jossa yksi sektori on korostettu leikkaamalla se irti.
Ympyrädiagrammi, jossa yksi sektori on korostettu leikkaamalla se irti. -
![Kolmiulotteinen ympyräkaavio, joka kuvaa Helsingin väestön jakautumista syntymäpaikan mukaan vuonna 2010. Kolmiulotteisessa ympyräkaaviossa sektoreiden pinta-alojen suhdetta on vaikeampi hahmottaa kuin kaksiulotteisessa[1].](//upload.wikimedia.org/wikipedia/commons/thumb/2/2a/Helsinki_Syntymapaikka_2010.svg/120px-Helsinki_Syntymapaikka_2010.svg.png) Kolmiulotteinen ympyräkaavio, joka kuvaa Helsingin väestön jakautumista syntymäpaikan mukaan vuonna 2010. Kolmiulotteisessa ympyräkaaviossa sektoreiden pinta-alojen suhdetta on vaikeampi hahmottaa kuin kaksiulotteisessa[1].
Kolmiulotteinen ympyräkaavio, joka kuvaa Helsingin väestön jakautumista syntymäpaikan mukaan vuonna 2010. Kolmiulotteisessa ympyräkaaviossa sektoreiden pinta-alojen suhdetta on vaikeampi hahmottaa kuin kaksiulotteisessa[1]. -
 Ympyräkaavio, jonka yhdestä pienestä sektorista on selvennyksen vuoksi tehty suurennos omaksi kaaviokseen.
Ympyräkaavio, jonka yhdestä pienestä sektorista on selvennyksen vuoksi tehty suurennos omaksi kaaviokseen. -
 Vierekkäisiä ympyräkaavioita, joiden koot kuvaavat määrien suhteita.
Vierekkäisiä ympyräkaavioita, joiden koot kuvaavat määrien suhteita.
Lähteet
- Karjalainen, Leila; Karjalainen, Juha: Tilastojen graafinen esittäminen. Pii-Kirjat, 2009. ISBN 978-952-9776-31-3.
- Kuusela, Vesa: Tilastografiikan perusteet. Edita, 2000. ISBN 951-37-3116-2.
Viitteet
- ↑ a b c d Karjalainen, s. 27.
- ↑ Kuusela, s. 145.
- ↑ a b Ian Spence, Stephan Lewandowsky: Displaying Proportions and Percentages (PDF) Applied Cognitive Psychology. 1991. ResearchGate. Viitattu 24.2.2013.
- ↑ Kuusela, s. 150.
- ↑ Michael Friendly: 1801, William Playfair, Pie chart Milestones in the history of thematic cartography, statistical graphics, and data visualization.. Viitattu 2.2.2015.
- ↑ Kuusela, s. 146–148.
- ↑ Kuusela, s. 148.
- ↑ Kuusela, s. 147.
- ↑ Kuusela, s. 149.
- ↑ Kuusela, s. 152.
Aiheesta muualla
 Kuvia tai muita tiedostoja aiheesta Ympyrädiagrammi Wikimedia Commonsissa
Kuvia tai muita tiedostoja aiheesta Ympyrädiagrammi Wikimedia Commonsissa




![Kolmiulotteinen ympyräkaavio, joka kuvaa Helsingin väestön jakautumista syntymäpaikan mukaan vuonna 2010. Kolmiulotteisessa ympyräkaaviossa sektoreiden pinta-alojen suhdetta on vaikeampi hahmottaa kuin kaksiulotteisessa[1].](http://upload.wikimedia.org/wikipedia/commons/thumb/2/2a/Helsinki_Syntymapaikka_2010.svg/120px-Helsinki_Syntymapaikka_2010.svg.png)










