Équilibre de phases

En physique, et plus particulièrement en thermodynamique, un équilibre de phases est un état de la matière dans lequel deux phases ou plus coexistent sans évolution.

Un diagramme de phases est un diagramme représentant les domaines d'existence et de coexistence des phases d'un corps pur ou d'un mélange en fonction des conditions opératoires de pression, température et composition. La règle des phases permet de déterminer le nombre maximal de phases pouvant coexister selon les conditions opératoires, ainsi que le nombre de conditions qu'un opérateur peut faire évoluer indépendamment l'une de l'autre sans provoquer de transition de phase.

Deux phases sont en équilibre si elles ont atteint simultanément :

• un équilibre mécanique : elles ont la même pression ;
• un équilibre thermique : elles ont la même température ;
• un équilibre diffusif : le potentiel chimique de chaque espèce chimique est homogène entre les deux phases.

Cette dernière condition est équivalente, pour chaque espèce, à l'homogénéité de sa fugacité entre les phases.

Sous l'hypothèse simplificatrice de la solution idéale, l'équilibre liquide-vapeur peut être calculé par les loi de Raoult et loi de Henry. L'équation de Schröder-van Laar permet de calculer les équilibres liquide-solide. Les lois permettant de calculer les propriétés colligatives donnent l'évolution des pression et température d'équilibre de phases d'un solvant liquide en présence d'un soluté très dilué.

Définitions

États et phases

États de la matière et changements d'état

• 
  Diagramme de phase de l'eau montrant l'état de l'eau pure en fonction de la température et de la pression. Au-delà du point critique, le liquide et la vapeur ne se distinguent plus. Au point triple les trois états coexistent.
• 
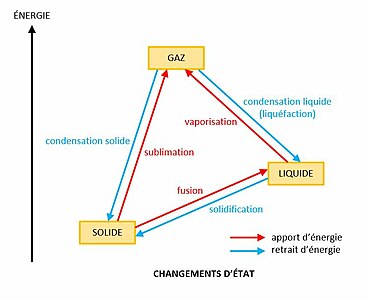  Principaux changements d'état de la matière. Un changement d'état implique une enthalpie de changement d'état.
• 
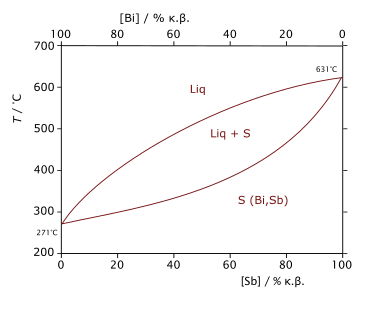  Diagramme de phase du mélange bismuth-antimoine montrant, en fonction de la température et de la composition, les domaines d'existence de l'état liquide (Liq), de l'état solide (S) et d'un domaine de coexistence des deux états liquide et solide (Liq+S).

Selon les conditions de pression, température et composition (conditions opératoires), la matière peut se présenter sous plusieurs formes appelées états de la matière, dont les principaux, étudiés en thermodynamique, sont le gaz, le liquide et le solide. L'eau, par exemple, peut se présenter sous forme de glace, qui est son état solide, de liquide, ou de vapeur, qui est son état gazeux. Aux hautes pressions et températures, au-delà du point critique, les états gazeux et liquide ne se distinguent plus^[1] : cet état est appelé état supercritique^[2]. Le point critique de l'eau se situe à 220,87 × 10⁵ Pa et 374,1 °C^[1].

Le passage d'un état à un autre est appelé changement d'état. Les principaux changements d'état sont^[3] : la vaporisation, de l'état liquide à l'état gazeux, la liquéfaction ou condensation liquide, de l'état gazeux à l'état liquide, la fusion, de l'état solide à l'état liquide, la solidification, de l'état liquide à l'état solide, la sublimation, de l'état solide à l'état gazeux, et la condensation solide, de l'état gazeux à l'état solide.

Un changement d'état d'un corps pur s'effectue à température et pression constantes. À température constante, un changement d'état d'un mélange s'effectue à pression variable ; à pression constante il s'effectue à température variable. Il existe des cas particuliers dans lesquels le changement d'état d'un mélange s'effectue à pression et température constantes, le mélange se comportant alors comme un corps purs : c'est notamment le cas des azéotropes pour les changements liquide-vapeur, et des points de fusion congruents pour les changements liquide-solide^[4]. Dans les hétéroazéotropes, un gaz se condense en deux phases liquides distinctes, de même que dans des eutectiques, un liquide se condense en deux phases solides distinctes.

Phases et transitions de phases

• 
  Diagramme de phases de l'eau : en bleu l'état solide, en vert l'état liquide, en orange l'état gazeux. Les chiffres romains correspondent aux diverses phases de glace (état solide).
• 
  Le diamant (à gauche) et le graphite (à droite) sont deux formes solides du carbone, constituant autant de phases solides distinctes. Dans les conditions de pression et température atmosphériques ordinaires, le graphite est stable, le diamant métastable.
• 
  Diagramme de phases cuivre-argent. ${\displaystyle \alpha }$ est une phase solide de cuivre contenant de l'argent, ${\displaystyle \beta }$ une phase solide d'argent contenant du cuivre. Les deux phases coexistent dans le domaine ${\displaystyle \alpha +\beta }$. Le point E est un eutectique.

Selon les conditions de pression, température et composition (conditions opératoires), un même état peut se présenter sous plusieurs formes appelées phases. Pour un corps pur (composé d'une seule espèce chimique) comme pour un mélange (composé de plusieurs espèces chimiques), il n'existe qu'une seule phase gazeuse : la diffusion de la matière induit naturellement que deux gaz mis en contact, quels qu'ils soient, se mélangent intimement pour former un système homogène.

Les corps purs ne présentent qu'une seule phase liquide, quelles que soient les conditions opératoires, à l'exception notable de certains isotopes de l'hélium présentant, en plus du liquide ordinaire, une phase liquide superfluide aux très basses températures (quelques kelvins)^[5]. Les mélanges peuvent présenter plusieurs phases liquides simultanément. Par exemple, un mélange d'huile et d'eau constitue deux phases liquides distinctes : une phase liquide organique et une phase liquide aqueuse non miscibles (dans les faits, chacune des deux phases contient une infime quantité de l'autre phase dissoute)^[6].

Les corps purs et les mélanges peuvent présenter plusieurs phases solides. L'eau pure solide (glace), par exemple, présente, selon les conditions opératoires, plus de onze formes cristallines qui constituent autant de phases solides distinctes^[7]. Les mélanges (alliages) de métaux présentent souvent, selon les conditions opératoires, de multiples formes cristallines qui sont autant de phases solides. La faculté d'un corps simple de se présenter sous plusieurs formes solides est appelée allotropie (cas du carbone avec, entre autres, le graphite et le diamant)^[8],[9], pour un corps composé elle est appelée polymorphisme (cas du carbonate de calcium avec l'aragonite, la calcite et la vatérite)^[9].

Lorsque les conditions opératoires sont modifiées, un matériau peut changer de phase. Ce changement est appelé transition de phase^[10]. Un changement d'état est une transition de phase, mais toutes les transitions de phase ne s'accompagnent pas nécessairement d'un changement d'état. Par exemple, la transition d'une forme de glace de l'eau à une autre est une transition de phase dans laquelle l'état de l'eau reste l'état solide.

Continuité, homogénéité et dispersion

• 
  Homogénéité
  Cette hypothèse est simplificatrice.
  Dans la colonne d'un baromètre à mercure, la pression est quasi nulle au sommet et égale à la pression atmosphérique au pied.
• 
  Dispersion
  Une phase n'est pas nécessairement d'un seul tenant.
  Un précipité est une phase solide dispersée dans une phase liquide en d'innombrables cristaux.
• 
  Continuité
  Une discontinuité de propriété lorsque l'on modifie une condition opératoire correspond à une transition de phase.
  Masse volumique de l'eau en fonction de la température. À 0 °C la masse volumique augmente brusquement : la glace (solide) fond et devient liquide. L'eau est un rare exemple de liquide plus dense que le solide (la glace flotte).

Une phase peut être définie comme une « partie d'un système qui, à l'échelle macroscopique, peut être considérée comme homogène^[11]. » Dans cette définition, les propriétés de la phase ne dépendent pas de la position dans la phase, et toute propriété a donc la même valeur en tout point du système. Ce n'est pas le cas dans la réalité. Par exemple, par effet de la gravité, la pression d'une colonne de fluide n'est pas la même en tête et en pied de colonne, ce qu'énonce la loi de l'hydrostatique. Cette différence de pression peut entrainer, surtout pour les fluides compressibles comme les gaz, une importante variation de masse volumique au long de la colonne. Dans une colonne d'eau liquide de 10 m, par exemple, la différence de pression est d'environ 1 bar entre le pied et la tête de la colonne ; si la pression en tête de colonne est la pression atmosphérique, une bulle d'air présente dans cette colonne a une masse volumique deux fois plus importante en pied qu'en tête. L'hypothèse de l'homogénéité des propriétés est raisonnable sur de petits volumes de phase dans lesquels, par exemple, l'effet de la loi de l'hydrostatique peut être négligée : dans un verre d'eau, la pression en fond de verre peut être considérée comme égale à la pression de surface. Cette hypothèse est généralement retenue en thermodynamique, étant donné que l'équilibre de phases est étudié dans les parages immédiats des interfaces entre ces phases ; de plus, dans le cadre d'une modélisation de la phase, elle permet de simplifier la mise en équation, en évitant de faire dépendre les propriétés du fluide de son emplacement dans l'espace. Toutefois, le système ne peut être trop petit, car à une certaine échelle l'effet de la tension superficielle ne peut plus être négligé et doit être pris en compte^[11].

Une phase peut cependant être dispersée dans une autre phase. Une phase dispersée se présente comme un ensemble de sous-domaines séparés les uns des autres par une autre phase et ayant tous les mêmes propriétés (état, pression, température, composition, forme cristalline, masse volumique, etc.). L'ensemble de ces sous-domaines est considéré comme une phase unique. Par exemple, un précipité ou une suspension est une phase solide divisée en petits éléments dans une phase liquide ; une émulsion est une phase liquide divisée en gouttelettes dans une autre phase liquide ; un aérosol est une phase liquide divisée en gouttelettes dans une phase gazeuse^[12].

Une phase peut aussi être définie comme un « arrangement des constituants d'un milieu dans lequel les propriétés mécaniques, thermodynamiques, électriques et magnétiques varient continûment^[13]. » La continuité signifie qu'il n'y a pas de « saut » de valeur d'une propriété de ce système si l'on modifie les conditions opératoires telles que la pression, la température ou la composition, aussi petite cette modification soit-elle. Un saut de valeur est caractéristique d'une transition de phase (voir la section Classification des transitions de phase). Par exemple, lorsque l'on comprime un gaz à température constante, sa masse volumique augmente continument. Lorsque la pression dépasse la pression de vapeur saturante du gaz, la masse volumique du système augmente fortement et brusquement : la phase n'est plus la même, le système est devenu liquide, de densité beaucoup plus importante que le gaz. De même, un matériau ferromagnétique ou ferrimagnétique dont on augmente la température perd brusquement son aimantation permanente à la température de Curie et devient paramagnétique^[14].

Équilibre et stabilité

Équilibre de phases

• 
  Équilibre liquide-vapeur du brome.
• 
  Deux phases liquides en équilibre : de l'huile (jaune, en haut) sur de l'eau (transparente, en bas).

Selon les conditions opératoires, un corps pur ou un mélange peut se présenter dans une phase ou une autre, voire sous plusieurs phases simultanément. La coexistence de plusieurs phases est appelée équilibre de phases. Les phases en équilibre peuvent être dans le même état ou dans des états différents. Lorsqu'une phase liquide est en équilibre avec une phase gazeuse, cette dernière est généralement appelée vapeur, l'équilibre est appelé équilibre liquide-vapeur plutôt que équilibre liquide-gaz. À pression atmosphérique normale (101 325 Pa), les phases solide (glace) et liquide de l'eau coexistent à 0 °C, ses phases gazeuse (vapeur d'eau) et liquide à 100 °C. Pour un corps pur les trois états coexistent de façon stable au point triple^[15], un unique couple de pression et de température : pour l'eau ce point se situe à 611,2 Pa et 0,01 °C^[15]. Plus généralement, le terme de point triple désigne tout point de coexistence de trois phases, quels que soient leurs états^[15]. Le diagramme de phase de l'eau montre plusieurs points triples en plus du point solide-liquide-vapeur : plusieurs points avec le liquide et deux formes de glace, et plusieurs points avec trois formes de glace.

Dans les équilibres de phases d'un mélange, les diverses phases ont le plus souvent des compositions différentes. Par exemple, un mélange d'huile et d'eau présente simultanément une phase liquide d'huile saturée en eau et une phase liquide aqueuse saturée en huile ; de même, un mélange d'eau et d'éthanol présente le plus souvent un équilibre liquide-vapeur dans lequel les deux phases ont des compositions différentes. Il existe des cas particuliers d'équilibre de phases d'un mélange dans lesquels les phases ont la même composition : c'est notamment le cas des azéotropes pour les équilibres liquide-vapeur et celui des points de fusion congruents pour les équilibres liquide-solide^[4].

Stabilité et métastabilité

• Exemple d'état métastable. La perturbation appliquée à cette eau liquide à température négative, en état de surfusion, déclenche son passage à l'état solide.
• 
  Diagramme de phases du carbone montrant les domaines de stabilité et de métastabilité du graphite et du diamant. La graphite est la forme stable dans les conditions atmosphériques.

De façon générale, un système thermodynamique présentant une ou plusieurs phases est dans un état d'équilibre dit stable s'il revient à cet équilibre après avoir subit une perturbation (un apport d'énergie relativement faible)^[16],[17]. À pression atmosphérique et 0 °C, si l'on agite brièvement de l'eau à son équilibre solide-liquide, cet équilibre n'est pas modifié (une agitation prolongée peut apporter suffisamment de chaleur au système pour provoquer la fonte de la glace).

Certains états observés se maintiennent dans le temps jusqu'à ce qu'une perturbation déclenche une transformation souvent violente : un tel état est dit métastable^[18]. La transformation observée consiste en l'établissement de la ou des phases stables dans les conditions opératoires données. Ainsi, l'eau peut être maintenue liquide en dessous de 0 °C à pression atmosphérique : cet état est appelé état de surfusion, il suffit alors de l'introduction d'une poussière ou d'une fluctuation de température pour que l'eau se solidifie brutalement ; cet état s'observe de façon naturelle lors des pluies verglaçantes. L'état métastable de l'eau non vaporisée au-dessus de 100 °C est appelé surébullition ou retard à l'ébullition ; il est observé dans une tasse de café chauffé au microonde qui entre en ébullition brutale lorsque l'on y ajoute du sucre^[19]. Dans les conditions de pression et température atmosphériques, le graphite est la forme solide stable du carbone, le diamant est métastable.

Diagramme de phases

Types de diagramme

• 
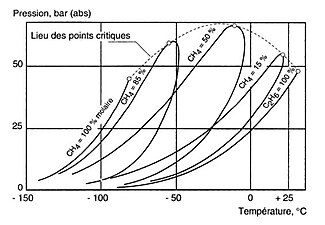  Diagramme de phases du mélange méthane (CH₄)-éthane (C₂H₆). Pression de changement d'état en fonction de la température, à compositions fixes.
• 
  Diagramme binaire isobare du mélange niobium (Nb)-antimoine (Sb). Température de changement d'état en fonction de la composition, à pression atmosphérique.
• 
  Diagramme isotherme du mélange chloroforme-éthanol. Pression de changement d'état en fonction de la composition à 20 °C.
• 
  Diagramme du mélange éthanol-acétate d'éthyle. Fraction molaire de l'éthanol en phase vapeur en fonction de la fraction molaire de l'éthanol en phase liquide à l'équilibre, à pression atmosphérique.
• 
  Diagramme ternaire du mélange plomb (Pb)-bismuth (Bi)-étain (Sn).

Un diagramme de phases représente les domaines d'existence des phases d'un matériau donné (corps pur ou mélange) en fonction des conditions opératoires qui déterminent l'existence de ces phases : la pression, la température et la composition. Les courbes qui délimitent ces domaines représentent les transitions de phases.

Pour un corps pur, un diagramme de phases représente la pression en fonction de la température. Un corps pur ne présente qu'une seule phase gazeuse et une seule phase liquide. Par contre, il peut présenter plusieurs phases solides^[20].

Pour un mélange, plusieurs types de diagrammes sont souvent utilisés :

• un diagramme représentant la pression en fonction de la température à composition constante ;
• un diagramme isobare, représentant, à pression donnée constante, l'évolution de la température en fonction de la composition ;
• un diagramme isotherme, représentant, à température donnée constante, l'évolution de la pression en fonction de la composition ;
• un diagramme représentant, pour deux phases en équilibre, la composition de l'une des phases en fonction de la composition de l'autre phase ; dans ce diagramme la pression ou la température est fixée.

Les pentes des courbes d'un diagramme représentant la pression en fonction de la température sont données théoriquement par la formule de Clapeyron ou par les formules d'Ehrenfest^[21].

Construction d'un diagramme isobare ou isotherme

L'exemple pris ici concerne un équilibre liquide-vapeur (gaz), mais peut être transposé à tout autre équilibre de phases. Le diagramme isotherme ci-contre a été construit pour deux corps (espèces chimiques), notés ${\displaystyle 1}$ et ${\displaystyle 2}$, de pressions de vapeur saturante respectives ${\displaystyle P_{1}}$ et ${\displaystyle P_{2}}$ à la température du diagramme. Avec ${\displaystyle P_{1}<P_{2}}$, le corps ${\displaystyle 2}$ est plus léger que le corps ${\displaystyle 1}$ : il se liquéfie à une pression plus élevée pour une même température.

Un diagramme isotherme représente, à température donnée constante, la pression en fonction de la composition d'un mélange. Un diagramme isobare représente, à pression donnée constante, la température en fonction de la composition d'un mélange. Ces deux types de diagramme sont utilisés pour des mélanges binaires (constitués de deux espèces chimiques). Les fractions molaires de ces deux espèces répondent donc à la contrainte ${\displaystyle x_{1}+x_{2}=1}$. Une courbe de pression ou de température peut ainsi n'être représentée qu'en fonction d'une seule de ces deux fractions : à température donnée ${\displaystyle P=P\!\left(x_{2}\right)}$, à pression donnée ${\displaystyle T=T\!\left(x_{2}\right)}$. Les courbes reportées sur ces diagrammes représentent les conditions opératoires dans lesquelles débutent les transitions de phase, elles délimitent les domaines d'existence des différentes phases du mélange. Un domaine du diagramme dans lequel n'existe qu'une seule phase est délimité par des courbes fonctions de la composition de cette phase. Par exemple, dans le diagramme ci-contre, le domaine d'existence de la phase liquide seule (aux hautes pressions) est délimité par la courbe de bulle (bleue) ${\displaystyle P=P\!\left(x_{2}^{\text{l}}\right)}$ tracée en fonction de la composition du liquide ; cette courbe représente les conditions de transition du liquide vers la vapeur dans lesquelles apparait la première bulle de gaz. Le domaine d'existence de la phase gaz seule (aux basses pressions) est délimité par la courbe de rosée (orange) ${\displaystyle P=P\!\left(x_{2}^{\text{g}}\right)}$ tracée en fonction de la composition du gaz ; cette courbe représente les conditions de transition de la vapeur vers le liquide dans lesquelles apparait la première goutte de liquide.

Entre deux domaines représentant des phases seules, il peut exister un domaine dans lequel les deux phases coexistent en équilibre. Par exemple, dans le diagramme ci-contre, il existe, entre les domaines du liquide seul et du gaz seul, un domaine dans lequel les deux phases coexistent. Dans ce type de domaine, les compositions des phases en équilibre sont données par les intersections des courbes limitrophes et de la droite horizontale isobare ou isotherme (selon le type de diagramme). Dans le diagramme ci-contre, au point ${\displaystyle {\mathsf {C}}}$ dans le domaine de coexistence des phases liquide et gaz, la composition de la phase liquide est donnée par le point ${\displaystyle {\mathsf {C}}^{\text{l}}}$ sur la courbe de bulle et la composition de la phase vapeur par le point ${\displaystyle {\mathsf {C}}^{\text{g}}}$ sur la courbe de rosée, les trois points étant à la même pression ${\displaystyle P_{\mathsf {C}}}$^[22]. Au point ${\displaystyle {\mathsf {C}}}$ le corps ${\displaystyle 2}$ a une fraction molaire ${\displaystyle x_{2}^{\text{l}}}$ en phase liquide et ${\displaystyle x_{2}^{\text{g}}}$ en phase gaz. Le point ${\displaystyle {\mathsf {C}}}$, lui, se situe à une fraction molaire ${\displaystyle x_{2}}$ comprise entre ${\displaystyle x_{2}^{\text{l}}}$ et ${\displaystyle x_{2}^{\text{g}}}$.

On suppose que le mélange est constitué d'une quantité de matière totale ${\displaystyle n}$, dont une quantité ${\displaystyle n_{2}}$ de l'espèce ${\displaystyle 2}$. On a par définition :

${\displaystyle x_{2}={n_{2} \over n}}$

Lorsque le mélange est biphasique, la quantité de matière se répartit entre une quantité ${\displaystyle n^{\text{l}}}$ en phase liquide, dont une quantité ${\displaystyle n_{2}^{\text{l}}}$ de l'espèce ${\displaystyle 2}$, et une quantité ${\displaystyle n^{\text{g}}}$ en phase vapeur, dont une quantité ${\displaystyle n_{2}^{\text{g}}}$ de l'espèce ${\displaystyle 2}$. Les bilans de matière donnent :

${\displaystyle n=n^{\text{l}}+n^{\text{g}}}$

${\displaystyle n_{2}=n_{2}^{\text{l}}+n_{2}^{\text{g}}}$

Les fractions molaires sont définies par :

${\displaystyle x_{2}^{\text{l}}={n_{2}^{\text{l}} \over n^{\text{l}}}}$

${\displaystyle x_{2}^{\text{g}}={n_{2}^{\text{g}} \over n^{\text{g}}}}$

En considérant les définitions des fractions molaires et les bilans de matière, on montre la règle des moments ou règle du levier^{[22],[23],[24],[25]} :

Règle des moments ou règle du levier : ${\displaystyle {\left[{\mathsf {C}}{\mathsf {C}}^{\text{l}}\right] \over \left[{\mathsf {C}}^{\text{g}}{\mathsf {C}}^{\text{l}}\right]}={x_{2}-x_{2}^{\text{l}} \over x_{2}^{\text{g}}-x_{2}^{\text{l}}}={n^{\text{g}} \over n^{\text{l}}+n^{\text{g}}}={n^{\text{g}} \over n}}$

Autrement dit, au point ${\displaystyle {\mathsf {C}}}$, le rapport des longueurs des segments de droite ${\displaystyle \left[{\mathsf {C}}{\mathsf {C}}^{\text{l}}\right]}$ et ${\displaystyle \left[{\mathsf {C}}^{\text{g}}{\mathsf {C}}^{\text{l}}\right]}$ permet de déterminer la proportion ${\displaystyle n^{\text{g}}/n}$ de gaz dans le mélange. Ce paramètre est appelé taux de vaporisation ou fraction de vapeur :

Taux de vaporisation ou fraction de vapeur : ${\displaystyle \tau ^{\text{g}}={n^{\text{g}} \over n^{\text{l}}+n^{\text{g}}}={n^{\text{g}} \over n}}$

On peut de même définir un taux de liquéfaction ou fraction de liquide : ${\displaystyle \tau ^{\text{l}}={\left[{\mathsf {C}}{\mathsf {C}}^{\text{g}}\right] \over \left[{\mathsf {C}}^{\text{l}}{\mathsf {C}}^{\text{g}}\right]}={n^{\text{l}} \over n}=1-\tau ^{\text{g}}}$.

Thermodynamique des équilibres de phases

Conditions d'équilibre

Conditions générales

Soit un système isolé (qui n'échange ni énergie ni matière avec l'extérieur) composé deux de phases, notées ${\displaystyle a}$ et ${\displaystyle b}$. Ce système subit une transformation afin d'atteindre l'équilibre. On écrit pour chacune des deux phases la variation d'énergie interne ${\displaystyle U}$^[26] :

${\displaystyle \mathrm {d} U^{a}=-P^{a}\,\mathrm {d} V^{a}+T^{a}\,\mathrm {d} S^{a}+\sum _{i=1}^{N}\mu _{i}^{a}\,\mathrm {d} n_{i}^{a}}$

${\displaystyle \mathrm {d} U^{b}=-P^{b}\,\mathrm {d} V^{b}+T^{b}\,\mathrm {d} S^{b}+\sum _{i=1}^{N}\mu _{i}^{b}\,\mathrm {d} n_{i}^{b}}$

avec ${\displaystyle X^{p}}$ la grandeur ${\displaystyle X}$ relative à la phase ${\displaystyle p}$. Soit, pour le système isolé global, les fonctions globales énergie interne globale ${\displaystyle U=U^{a}+U^{b}}$, entropie globale ${\displaystyle S=S^{a}+S^{b}}$, volume global ${\displaystyle V=V^{a}+V^{b}}$ et quantité globale ${\displaystyle n_{i}=n_{i}^{a}+n_{i}^{b}}$ de chacun des ${\displaystyle N}$ corps ${\displaystyle i}$. On a les relations sur le système global isolé, en l'absence de réaction chimique^[26] :

• ${\displaystyle \mathrm {d} U=\mathrm {d} U^{a}+\mathrm {d} U^{b}=0}$ (premier principe de la thermodynamique) ;
• ${\displaystyle \mathrm {d} S=\mathrm {d} S^{a}+\mathrm {d} S^{b}\geq 0}$ (deuxième principe de la thermodynamique) ;
• ${\displaystyle \mathrm {d} V=\mathrm {d} V^{a}+\mathrm {d} V^{b}=0}$ (absence de travail des forces de pression) ;
• ${\displaystyle \mathrm {d} n_{i}=\mathrm {d} n_{i}^{a}+\mathrm {d} n_{i}^{b}=0}$ pour tout ${\displaystyle i\in [1,\cdots ,N]}$ (conservation de la matière).

Les grandeurs globales du système global isolé (de l'ensemble constitué par les deux phases) sont constantes (hormis l'entropie), mais les grandeurs propres à chacun des deux phases, elles, peuvent varier au cours de la transformation, leurs variations étant opposées. Par exemple, le volume global du système isolé, ${\displaystyle V=V^{a}+V^{b}}$, est constant, mais les volumes des phases ${\displaystyle V^{a}}$ et ${\displaystyle V^{b}}$ peuvent varier et ${\displaystyle \mathrm {d} V^{b}=-\mathrm {d} V^{a}}$.

On obtient les relations globales d'évolution du système isolé :

${\displaystyle \mathrm {d} U=-\left(P^{a}-P^{b}\right)\,\mathrm {d} V^{a}+T^{a}\,\mathrm {d} S^{a}+T^{b}\,\mathrm {d} S^{b}+\sum _{i=1}^{N}\left(\mu _{i}^{a}-\mu _{i}^{b}\right)\,\mathrm {d} n_{i}^{a}=0}$ ${\displaystyle \mathrm {d} S=\mathrm {d} S^{a}+\mathrm {d} S^{b}\geq 0}$

L'équilibre est atteint lorsque l'entropie globale du système atteint un maximum. Les variations d'entropie des deux phases sont alors liées par : ${\displaystyle \mathrm {d} S=\mathrm {d} S^{a}+\mathrm {d} S^{b}=0}$. On peut donc écrire pour le système global à l'équilibre^[27],[26] :

${\displaystyle \mathrm {d} U=-\left(P^{a}-P^{b}\right)\,\mathrm {d} V^{a}+\left(T^{a}-T^{b}\right)\,\mathrm {d} S^{a}+\sum _{i=1}^{N}\left(\mu _{i}^{a}-\mu _{i}^{b}\right)\,\mathrm {d} n_{i}^{a}=0}$

Quand les deux phases sont à l'équilibre, cela ne signifie pas qu'il n'y a pas d'échanges entre elles. Les deux phases continuent à échanger de la matière et de l'énergie, mais globalement les échanges se font dans les deux sens et se compensent : l'état d'équilibre obtenu est qualifié de dynamique ou stationnaire. Les variations ${\displaystyle \mathrm {d} V^{a}}$, ${\displaystyle \mathrm {d} S^{a}}$ et ${\displaystyle \mathrm {d} n_{i}^{a}}$ pour tout ${\displaystyle i\in [1,\cdots ,N]}$ sont donc non nulles à l'équilibre. La relation précédente implique par conséquent l'homogénéité des potentiels mécanique (pression), thermique (température) et chimiques (potentiels chimiques) entre les deux phases à l'équilibre^[26] :

• ${\displaystyle P^{a}=P^{b}}$ ;
• ${\displaystyle T^{a}=T^{b}}$ ;
• ${\displaystyle \mu _{i}^{a}=\mu _{i}^{b}}$ pour tout ${\displaystyle i\in [1,\cdots ,N]}$.

Les conditions d'équilibre sont donc données par^{[26],[28],[29]} :

Conditions d'équilibre de deux phases ${\displaystyle a}$ et ${\displaystyle b}$

Équilibre mécanique	homogénéité de la pression ${\displaystyle P}$
Équilibre thermique	homogénéité de la température ${\displaystyle T}$
Équilibre diffusif	homogénéité des potentiels chimiques pour tout corps ${\displaystyle i}$ : ${\displaystyle \mu _{i}^{a}=\mu _{i}^{b}}$

Si le système contient une troisième phase ${\displaystyle c}$, celle-ci doit être à l'équilibre avec les phases ${\displaystyle a}$ et ${\displaystyle b}$ : elle sera par conséquent à l'équilibre aux mêmes pression, température et potentiels chimiques. Ces conditions sont donc généralisables à plus de deux phases en équilibre (équilibres gaz-liquide-liquide ou gaz-liquide-solide par exemple, ou multiples phases liquides^[6] ou solides).

Note sur l'homogénéité des potentiels chimiques

L'homogénéité des potentiels chimiques signifie que pour le corps 1 ${\displaystyle \mu _{1}^{a}=\mu _{1}^{b}}$, pour le corps 2 ${\displaystyle \mu _{2}^{a}=\mu _{2}^{b}}$, … , pour le corps ${\displaystyle N}$ ${\displaystyle \mu _{N}^{a}=\mu _{N}^{b}}$, mais pas que ces potentiels sont égaux entre corps différents : ${\displaystyle \mu _{1}^{a}\neq \mu _{2}^{a}\neq \cdots \neq \mu _{N}^{a}}$.

Homogénéité des fugacités

Dans n'importe quelle phase ${\displaystyle p}$, la fugacité ${\displaystyle f_{i}^{p}}$ du corps ${\displaystyle i}$ est définie par la relation entre potentiels chimiques :

${\displaystyle \mu _{i}^{p}-\mu _{i}^{\bullet ,*}=RT\,\ln \!\left({f_{i}^{p} \over P}\right)}$

avec :

La fugacité ${\displaystyle f_{i}^{p}}$ lie les propriétés d'un corps ${\displaystyle i}$, pur ou en mélange, dans une phase ${\displaystyle p}$ quelconque réelle, aux propriétés de ce même corps à l'état de gaz parfait pur aux mêmes pression et température que la phase réelle. On peut écrire pour deux phases ${\displaystyle a}$ et ${\displaystyle b}$ en équilibre, en introduisant les fugacités respectives ${\displaystyle f_{i}^{a}}$ et ${\displaystyle f_{i}^{b}}$ de tout corps ${\displaystyle i}$ :

${\displaystyle \mu _{i}^{a}=\mu _{i}^{\bullet ,*}+RT\,\ln \!\left({f_{i}^{a} \over P}\right)}$

${\displaystyle \mu _{i}^{b}=\mu _{i}^{\bullet ,*}+RT\,\ln \!\left({f_{i}^{b} \over P}\right)}$

À l'équilibre, les deux phases ${\displaystyle a}$ et ${\displaystyle b}$ sont aux mêmes pression et température, en conséquence le potentiel ${\displaystyle \mu _{i}^{\bullet ,*}}$ est le même dans ces deux relations, et l'on peut écrire, en considérant que ${\displaystyle \mu _{i}^{a}=\mu _{i}^{b}}$^{[29],[30],[31]} :

Condition d'équilibre des phases : ${\displaystyle f_{i}^{a}=f_{i}^{b}}$

En termes de condition d'équilibre des phases, l'égalité des fugacités est donc équivalente à l'égalité des potentiels chimiques : si l'une est vérifiée, alors l'autre est aussi vérifiée, et réciproquement. Néanmoins, les potentiels chimiques ne pouvant être déterminés qu'à une constante additive près, l'égalité des potentiels chimiques est difficilement utilisable, tandis que les fugacités peuvent être déterminées de façon absolue, ce qui les rend particulièrement utiles.

Règle des phases

Soit un mélange quelconque composé de ${\displaystyle N}$ espèces chimiques réparties en ${\displaystyle p}$ phases. Les conditions d'équilibre stable d'un système hétérogène définies plus haut impliquent que :

• les ${\displaystyle p}$ pressions sont liées par les ${\displaystyle p-1}$ égalités :

${\displaystyle P^{a}=P^{b}=\cdots =P^{p}}$

• les ${\displaystyle p}$ températures sont liées par les ${\displaystyle p-1}$ égalités :

${\displaystyle T^{a}=T^{b}=\cdots =T^{p}}$

• pour chacun des ${\displaystyle N}$ constituants, les ${\displaystyle p}$ potentiels chimiques sont liés par les ${\displaystyle p-1}$ égalités :

${\displaystyle {\begin{cases}\mu _{1}^{a}=\mu _{1}^{b}=\cdots =\mu _{1}^{p}\\\mu _{2}^{a}=\mu _{2}^{b}=\cdots =\mu _{2}^{p}\\\cdots \\\mu _{N}^{a}=\mu _{N}^{b}=\cdots =\mu _{N}^{p}\end{cases}}}$

Pour chaque phase, les diverses variables sont également liées par la relation de Gibbs-Duhem, soit ${\displaystyle p}$ équations supplémentaires :

${\displaystyle {\begin{cases}V^{a}\,\mathrm {d} P^{a}-S^{a}\,\mathrm {d} T^{a}=\sum _{i=1}^{N}n_{i}^{a}\,\mathrm {d} \mu _{i}^{a}\\V^{b}\,\mathrm {d} P^{b}-S^{b}\,\mathrm {d} T^{b}=\sum _{i=1}^{N}n_{i}^{b}\,\mathrm {d} \mu _{i}^{b}\\\cdots \\V^{p}\,\mathrm {d} P^{p}-S^{p}\,\mathrm {d} T^{p}=\sum _{i=1}^{N}n_{i}^{p}\,\mathrm {d} \mu _{i}^{p}\end{cases}}}$

On a donc un total de ${\displaystyle X=\left(2+N\right)p}$ variables et ${\displaystyle Y=\left(2+N\right)\left(p-1\right)+p}$ équations. La variance ${\displaystyle v=X-Y}$ indique le nombre de variables, c'est-à-dire le nombre de conditions opératoires (parmi la pression, la température et les compositions des phases), que l'opérateur peut fixer indépendamment l'une de l'autre en restant dans le domaine d'équilibre stable des phases, d'où la règle des phases^[13],[32] :

Règle des phases : ${\displaystyle v=N+2-p}$

Par exemple, pour un corps pur, soit ${\displaystyle N=1}$ :

• en présence d'une seule phase (par exemple un liquide seul), soit ${\displaystyle p=1}$, on a ${\displaystyle v=2}$ : l'opérateur peut imposer la pression et la température indépendamment l'une de l'autre ;
• en présence de deux phases (par exemple un équilibre liquide-gaz), soit ${\displaystyle p=2}$, on a ${\displaystyle v=1}$ : l'opérateur peut imposer la pression mais la température d'équilibre est subie (et inversement) ;
• en présence de trois phases (par exemple le point triple de l'équilibre solide-liquide-gaz), soit ${\displaystyle p=3}$, on a ${\displaystyle v=0}$ : l'opérateur ne peut imposer aucune condition de l'équilibre.

Un mélange de ${\displaystyle N}$ constituants peut au plus se présenter sous ${\displaystyle p=N+2}$ phases à l'équilibre stable. Il ne peut y avoir au plus qu'une seule phase gaz, mais il peut y avoir plusieurs phases liquides et solides à l'équilibre^[6].

Théorème de Gibbs-Konovalov

• 
  Diagramme de phases isobare d'un azéotrope négatif. Au maximum des courbes de température, les compositions des deux phases sont identiques.
• 
  Diagramme de phases du mélange chlorure d'hydrogène (HCl) - eau (H₂O) montrant quatre points de fusion congruents à −70 °C, −25 °C, −18 °C et −15 °C.

Dans un diagramme de phases isobare ou isotherme d'un mélange, les courbes de transition de phase peuvent présenter des extrémums (maximum ou minimum), respectivement de pression ou de température, en fonction de la composition. Le théorème de Gibbs-Konovalov établit que^[33],[34] :

« Aux points d'extrémum de pression ou de température, les phases en équilibre ont la même composition. »

— Théorème de Gibbs-Konovalov

Dans le diagramme de phases d'un équilibre liquide-vapeur, par exemple, si la courbe de bulle atteint un extrémum, alors la courbe de rosée atteint un extrémum à la même composition. Pour la pression et la température considérées, les phases liquide et vapeur en équilibre ont la même composition, et le mélange se comporte comme un corps pur : il s'agit d'un azéotrope. Dans un équilibre liquide-solide, ce cas de figure est appelé point de fusion congruent.

Stabilité d'un équilibre

Le deuxième principe de la thermodynamique induit qu'un système à l'équilibre n'est stable que si l'entropie ${\displaystyle S}$ est maximale. Ceci induit que, pour un système à pression et température données, l'enthalpie libre ${\displaystyle G}$ est minimale. Ce principe implique également que l'entropie est une fonction concave de ses variables, et l'enthalpie libre, à pression et température données, une fonction convexe de ses variables.

L'entropie dans un changement d'état

On apporte, à pression ${\displaystyle P}$ et quantité de matière ${\displaystyle n}$ constantes, de la chaleur ${\displaystyle Q}$ à un corps pur dans un récipient fermé de volume ${\displaystyle V}$ pouvant varier. L'énergie interne ${\displaystyle U}$ du corps pur, en présence du travail des seules forces de pression, évolue selon le premier principe de la thermodynamique :

${\displaystyle \mathrm {d} U=-P\,\mathrm {d} V+\delta Q_{P,n}}$

En introduisant l'enthalpie ${\displaystyle H=U+PV}$, on a, à pression ${\displaystyle P}$ constante :

${\displaystyle \delta Q_{P,n}=\mathrm {d} U+P\,\mathrm {d} V=\mathrm {d} \left[U+PV\right]=\mathrm {d} H}$

La transformation est réversible, on introduit l'entropie ${\displaystyle S}$ :

${\displaystyle \delta Q_{P,n}=T\,\mathrm {d} S}$

La chaleur apportée au corps pur est donc liée à l'entropie et à l'enthalpie selon :

${\displaystyle \delta Q_{P,n}=T\,\mathrm {d} S=\mathrm {d} H}$

Puisque la température thermodynamique ${\displaystyle T}$ est positive, on obtient :

(a) : ${\displaystyle \left({\partial S \over \partial H}\right)_{P,n}={1 \over T}>0}$

La transformation ayant lieu à pression et quantité de matière constantes, on a par définition de la capacité thermique isobare ${\displaystyle C_{P}}$ :

${\displaystyle C_{P}=T\,\left({\partial S \over \partial T}\right)_{P,n}=\left({\partial H \over \partial S}\right)_{P,n}\,\left({\partial S \over \partial T}\right)_{P,n}=\left({\partial H \over \partial T}\right)_{P,n}}$

On peut donc écrire la dérivée seconde :

${\displaystyle \left({\partial ^{2}S \over {\partial H}^{2}}\right)_{P,n}=\left({\partial \over \partial H}\left({\partial S \over \partial H}\right)_{P,n}\right)_{P,n}=\left({\partial {1 \over T} \over \partial H}\right)_{P,n}=-{1 \over T^{2}}\,\left({\partial T \over \partial H}\right)_{P,n}=-{1 \over C_{P}\,T^{2}}}$

Les conditions de stabilité thermodynamique donnent^[35] ${\displaystyle C_{P}\geq 0}$. On obtient :

(b) : ${\displaystyle \left({\partial ^{2}S \over {\partial H}^{2}}\right)_{P,n}=-{1 \over C_{P}\,T^{2}}\leq 0}$

Les équations (a) et (b) montrent que, à pression et composition constantes, l'entropie ${\displaystyle S}$ est une fonction croissante concave de l'enthalpie ${\displaystyle H}$.

Sur la figure ci-contre, la courbe ABC bleue représente l'évolution, à pression et quantité de matière constantes, de l'entropie d'un corps pur dans une phase ${\displaystyle a}$, la courbe CDE orange celle du même corps pur dans une phase ${\displaystyle b}$. Les deux courbes sont concaves : si l'on joint deux points bleus, ou deux points orange, par un segment de droite, celui-ci est en-dessous de la courbe considérée. Cependant, la courbe globale ABCDE n'est pas dérivable au point C. De plus, elle est localement convexe entre B et D : si l'on joint un point de BC à un point de CD par un segment de droite, celui-ci est au-dessus de la courbe. Entre les points B et D, le corps pur ne peut être en équilibre stable s'il suit la courbe BCD. Pour conserver ses propriétés de continuité, dérivabilité et concavité, l'entropie passe par le segment de droite BD gris. Au point B le segment gris est tangent à la courbe bleue, au point D il est tangent à la courbe orange. La courbe ABDE est globalement dérivable et concave, contrairement à la courbe ABCDE. Le segment BD est la seule trajectoire qui rend l'entropie globalement dérivable et concave de A à E, tout autre point que B ou D, toute autre courbe qu'un segment de droite entre ces deux points engendre une courbe d'entropie localement non dérivable ou convexe^[36].

Aux basses enthalpies, en amont du point B, le corps pur est exclusivement en phase ${\displaystyle a}$. En aval du point D, aux hautes enthalpies, le corps pur est exclusivement en phase ${\displaystyle b}$. Entre B et D, pour une enthalpie donnée, le segment gris représente une entropie supérieure aux entropies des phases ${\displaystyle a}$ et ${\displaystyle b}$ seules représentées respectivement par les courbes bleue et orange : cette entropie maximale dans ces conditions de pression et température représente le point de stabilité du système, mais ne représente pas une phase seule. Entre B et D, le corps pur subit un changement d'état et les deux phases ${\displaystyle a}$ et ${\displaystyle b}$, à enthalpie donnée, coexistent en un équilibre stable^[36].

La relation ${\displaystyle \mathrm {d} H=T\,\mathrm {d} S}$ induit que sur le segment BD la température est constante : à la pression donnée, les deux phases du corps pur ne peuvent coexister qu'à une seule température, conformément à la règle des phases. Ainsi, les grandeurs ${\displaystyle S^{\boldsymbol {\mathsf {B}}}}$, ${\displaystyle H^{\boldsymbol {\mathsf {B}}}}$, ${\displaystyle S^{\boldsymbol {\mathsf {D}}}}$ et ${\displaystyle H^{\boldsymbol {\mathsf {D}}}}$ sont établies aux mêmes pression ${\displaystyle P}$, température ${\displaystyle T_{a\to b}}$ et quantité de matière ${\displaystyle n}$. La température de changement d'état est donnée par le rapport^[36] :

Température de changement d'état : ${\displaystyle T_{a\to b}={H^{\boldsymbol {\mathsf {D}}}-H^{\boldsymbol {\mathsf {B}}} \over S^{\boldsymbol {\mathsf {D}}}-S^{\boldsymbol {\mathsf {B}}}}}$

L'écart ${\displaystyle S^{\boldsymbol {\mathsf {D}}}-S^{\boldsymbol {\mathsf {B}}}}$ rapporté à la quantité de matière totale ${\displaystyle n}$ mise en jeu est l'entropie de changement d'état du corps pur. L'écart ${\displaystyle H^{\boldsymbol {\mathsf {D}}}-H^{\boldsymbol {\mathsf {B}}}}$ rapporté à la quantité de matière totale ${\displaystyle n}$ mise en jeu est l'enthalpie de changement d'état du corps pur^[36]. L'enthalpie de changement d'état est la chaleur qu'il faut apporter à une mole de corps pur pour passer entièrement d'un état à l'autre :

Entropie de changement d'état : ${\displaystyle \Delta _{a\to b}S={S^{\boldsymbol {\mathsf {D}}}-S^{\boldsymbol {\mathsf {B}}} \over n}}$ Enthalpie de changement d'état : ${\displaystyle \Delta _{a\to b}H={H^{\boldsymbol {\mathsf {D}}}-H^{\boldsymbol {\mathsf {B}}} \over n}=T_{a\to b}\,\Delta _{a\to b}S}$

L'équation du segment BD gris s'écrit :

${\displaystyle S=\left(1-\tau ^{b}\right)\times S^{\boldsymbol {\mathsf {B}}}+\tau ^{b}\times S^{\boldsymbol {\mathsf {D}}}}$

${\displaystyle H=\left(1-\tau ^{b}\right)\times H^{\boldsymbol {\mathsf {B}}}+\tau ^{b}\times H^{\boldsymbol {\mathsf {D}}}}$

Les points B et D représentant la même quantité ${\displaystyle n}$ de corps pur, on peut écrire, en introduisant les grandeurs molaires respectives :

${\displaystyle S=\left(1-\tau ^{b}\right)n\times {\bar {S}}^{\boldsymbol {\mathsf {B}}}+\tau ^{b}\,n\times {\bar {S}}^{\boldsymbol {\mathsf {D}}}}$

${\displaystyle H=\left(1-\tau ^{b}\right)n\times {\bar {H}}^{\boldsymbol {\mathsf {B}}}+\tau ^{b}\,n\times {\bar {H}}^{\boldsymbol {\mathsf {D}}}}$

Pour ${\displaystyle \tau ^{b}=0}$ le corps pur est au point B, entièrement en phase ${\displaystyle a}$ ; pour ${\displaystyle \tau ^{b}=1}$ il est au point D, entièrement en phase ${\displaystyle b}$. Pour ${\displaystyle 0<\tau ^{b}<1}$ le corps pur est biphasique, entre B et D : une quantité ${\displaystyle n^{a}=\left(1-\tau ^{b}\right)n}$ de phase ${\displaystyle a}$ coexiste en un équilibre stable avec une quantité ${\displaystyle n^{b}=\tau ^{b}\,n}$ de phase ${\displaystyle b}$. Le paramètre ${\displaystyle \tau ^{b}}$ est le taux de changement d'état, ou fraction de phase ${\displaystyle b}$, c'est-à-dire la quantité de phase ${\displaystyle b}$ rapportée à la quantité de matière totale ${\displaystyle n}$ mise en jeu lors de la transformation :

Taux de changement d'état ou fraction de phase : ${\displaystyle \tau ^{b}={n^{b} \over n^{a}+n^{b}}={n^{b} \over n}}$

Autrement dit, si l'on dispose, à la pression ${\displaystyle P}$ et la température ${\displaystyle T_{a\to b}}$, d'une part d'une quantité ${\displaystyle n}$ de corps pur en phase ${\displaystyle a}$ et que l'on en prélève une fraction ${\displaystyle 1-\tau ^{b}}$, et d'autre part d'une quantité ${\displaystyle n}$ de corps pur en phase ${\displaystyle b}$ et que l'on en prélève une fraction ${\displaystyle \tau ^{b}}$, si l'on met en contact ces deux fractions, alors celles-ci sont d'emblée en équilibre stable, sans nécessité d'une transformation pour atteindre cet équilibre^[37].

Les branches BC bleue et CD orange sont des branches de métastabilité des phases correspondantes. Si le corps pur évolue sur ces branches (y compris au-delà de C pour la phase ${\displaystyle a}$ et en deçà de C pour la phase ${\displaystyle b}$), la moindre perturbation peut provoquer un brusque changement d'état, amenant l'entropie sur la courbe ABDE stable, à enthalpie constante^[36]. L'état métastable d'un liquide non solidifié en dessous de sa température de fusion est appelé surfusion, il s'observe de façon naturelle pour l'eau lors des pluies verglaçantes (voir également la vidéo présentée dans la section Stabilité et métastabilité). L'état métastable d'un liquide non vaporisé au-dessus de sa température d'ébullition est appelé surébullition ou retard à l'ébullition, il s'observe dans une tasse de café chauffé au microonde qui entre en ébullition brutale lorsque l'on y ajoute du sucre^[19].

Le même raisonnement peut être tenu pour les changements d'état des mélanges ; il doit cependant être tenu compte de la variation des compositions des phases en cours de transition.

Équilibre de phases selon la composition

On considère un mélange constitué de deux espèces chimiques notées ${\displaystyle 1}$ et ${\displaystyle 2}$. Si l'on fait varier la pression, la température et la composition du mélange, l'énergie interne du système varie selon :

${\displaystyle \mathrm {d} U=-P\,\mathrm {d} V+T\,\mathrm {d} S+\mu _{1}\,\mathrm {d} n_{1}+\mu _{2}\,\mathrm {d} n_{2}}$

avec :

• ${\displaystyle n_{1}}$ et ${\displaystyle n_{2}}$ les quantités totales respectives de ${\displaystyle 1}$ et ${\displaystyle 2}$ dans le mélange ;
• ${\displaystyle \mu _{1}}$ et ${\displaystyle \mu _{2}}$ les potentiels chimiques respectifs des deux corps.

Par la suite, on considère une transformation à pression et température données, seule la variation de la composition est étudiée. À pression et température constantes, on introduit l'enthalpie libre ${\displaystyle G=U+PV-TS}$ et la relation précédente devient :

${\displaystyle \mathrm {d} U+P\,\mathrm {d} V-T\,\mathrm {d} S=\mathrm {d} \left[U+PV-TS\right]=\mathrm {d} G=\mu _{1}\,\mathrm {d} n_{1}+\mu _{2}\,\mathrm {d} n_{2}}$

Le théorème d'Euler permet d'écrire, en introduisant l'enthalpie libre molaire ${\displaystyle {\bar {G}}}$ et les fractions molaires ${\displaystyle x_{1}}$ et ${\displaystyle x_{2}}$ :

${\displaystyle G=n_{1}\,\mu _{1}+n_{2}\,\mu _{2}}$

${\displaystyle {\bar {G}}=x_{1}\,\mu _{1}+x_{2}\,\mu _{2}}$

À pression et température constantes, le deuxième principe de la thermodynamique induit que l'enthalpie libre ne peut que décroître lors d'une transformation spontanée ; à l'équilibre, l'enthalpie libre atteint un minimum. Lorsque l'on mélange deux corps purs, l'enthalpie libre du mélange résultant ne peut donc être, à l'équilibre, qu'inférieure à la somme des enthalpies libres des corps purs considérés séparément, soit :

${\displaystyle {\bar {G}}\leq x_{1}\,\mu _{1}^{*}+x_{2}\,\mu _{2}^{*}}$

avec ${\displaystyle \mu _{1}^{*}}$ et ${\displaystyle \mu _{2}^{*}}$ les potentiels chimiques des deux corps purs. Un mélange tel que ${\displaystyle {\bar {G}}>x_{1}\,\mu _{1}^{*}+x_{2}\,\mu _{2}^{*}}$ est instable^[38]. Une grandeur molaire n'est fonction que de la pression, de la température et des fractions molaires : ${\displaystyle {\bar {G}}={\bar {G}}\!\left(P,T,x_{1},x_{2}\right)}$. Pour un mélange binaire, les deux fractions étant liées par la relation ${\displaystyle x_{1}+x_{2}=1}$, on peut écrire la fonction comme ne dépendant, arbitrairement, que de ${\displaystyle x_{2}}$ pour la composition : ${\displaystyle {\bar {G}}={\bar {G}}\!\left(P,T,x_{2}\right)}$. Ceci permet de tracer des diagrammes à pression et température constantes comme celui de la figure ci-contre. À pression et température données, l'enthalpie libre est une fonction continue, dérivable et convexe selon la composition pour tout ${\displaystyle 0\leq x_{2}\leq 1}$^[38].

On suppose que le mélange binaire peut se présenter, aux pression et température données, sous une phase ${\displaystyle a}$ ou une phase ${\displaystyle b}$ selon la composition du mélange. Soient ${\displaystyle {\bar {G}}^{a}}$ et ${\displaystyle {\bar {G}}^{b}}$ leurs enthalpies libres molaires respectives^[38] :

${\displaystyle {\bar {G}}^{a}=x_{1}\,\mu _{1}^{a}+x_{2}\,\mu _{2}^{a}}$

${\displaystyle {\bar {G}}^{b}=x_{1}\,\mu _{1}^{b}+x_{2}\,\mu _{2}^{b}}$

La figure ci-contre donne un exemple de diagramme représentant simultanément deux courbes ${\displaystyle {\bar {G}}^{a}}$ et ${\displaystyle {\bar {G}}^{b}}$ représentatives de la plupart des fonctions de ce type. Ces deux courbes sont continues, dérivables et convexes pour toutes les compositions.

Pour une composition donnée (une valeur de ${\displaystyle x_{2}}$), la phase stable est la phase ayant une enthalpie libre minimale. Pour les faibles valeurs de ${\displaystyle x_{2}}$, entre les points A et B, on a ${\displaystyle {\bar {G}}^{a}<{\bar {G}}^{b}}$, c'est donc la phase ${\displaystyle a}$ qui est stable et ${\displaystyle {\bar {G}}={\bar {G}}^{a}}$. Pour les fortes valeurs de ${\displaystyle x_{2}}$, entre les points D et E, on a ${\displaystyle {\bar {G}}^{b}<{\bar {G}}^{a}}$, c'est donc la phase ${\displaystyle b}$ qui est stable et ${\displaystyle {\bar {G}}={\bar {G}}^{b}}$^[38].

Entre les points B et D, si l'on suit le même raisonnement, la fonction ${\displaystyle {\bar {G}}}$ devrait passer par le point C et ne serait plus dérivable ni convexe. La fonction passe par le segment gris BD, tangent aux deux courbes en ces points : ce segment est la seule fonction qui permet de rendre l'enthalpie libre continue, dérivable et convexe sur toutes les compositions^[38]. Entre B et D les deux phases ${\displaystyle a}$ et ${\displaystyle b}$ sont en équilibre^[38],[39]. Par exemple, pour la composition ${\displaystyle x_{2}}$ donnée sur le graphe, on a ${\displaystyle {\bar {G}}^{b}<{\bar {G}}^{a}}$, mais la phase ${\displaystyle b}$ est métastable : le mélange n'est stable que sous la forme d'un équilibre des deux phases représenté par le point P sur le segment gris, auquel ${\displaystyle {\bar {G}}<{\bar {G}}^{b}}$. À cet équilibre, la phase ${\displaystyle a}$ a la composition ${\displaystyle x_{2}^{\boldsymbol {\mathsf {B}}}}$ du point B et la phase ${\displaystyle b}$ la composition ${\displaystyle x_{2}^{\boldsymbol {\mathsf {D}}}}$ du point D. Avec la composition ${\displaystyle x_{2}}$, la règle des moments donne la fraction de phase^[38],[39] :

Fraction de phase ${\displaystyle b}$ : ${\displaystyle \tau ^{b}={n^{b} \over n^{a}+n^{b}}={n^{b} \over n_{1}+n_{2}}={x_{2}-x_{2}^{\boldsymbol {\mathsf {B}}} \over x_{2}^{\boldsymbol {\mathsf {D}}}-x_{2}^{\boldsymbol {\mathsf {B}}}}}$

avec ${\displaystyle n^{a}}$ et ${\displaystyle n^{b}}$ les quantités respectives des phases ${\displaystyle a}$ et ${\displaystyle b}$. Entre les points B et D on a par conséquent^[38],[39] :

${\displaystyle {\bar {G}}=\left(1-\tau ^{b}\right)\times {\bar {G}}^{\boldsymbol {\mathsf {B}}}+\tau ^{b}\times {\bar {G}}^{\boldsymbol {\mathsf {D}}}}$

avec les enthalpies libres respectives aux points B et D :

${\displaystyle {\bar {G}}^{\boldsymbol {\mathsf {B}}}={\bar {G}}^{a}\!\left(x_{2}^{\boldsymbol {\mathsf {B}}}\right)=\left(1-x_{2}^{\boldsymbol {\mathsf {B}}}\right)\,\mu _{1}^{a}\!\left(x_{2}^{\boldsymbol {\mathsf {B}}}\right)+x_{2}^{\boldsymbol {\mathsf {B}}}\,\mu _{2}^{a}\!\left(x_{2}^{\boldsymbol {\mathsf {B}}}\right)}$

${\displaystyle {\bar {G}}^{\boldsymbol {\mathsf {D}}}={\bar {G}}^{b}\!\left(x_{2}^{\boldsymbol {\mathsf {D}}}\right)=\left(1-x_{2}^{\boldsymbol {\mathsf {D}}}\right)\,\mu _{1}^{b}\!\left(x_{2}^{\boldsymbol {\mathsf {D}}}\right)+x_{2}^{\boldsymbol {\mathsf {D}}}\,\mu _{2}^{b}\!\left(x_{2}^{\boldsymbol {\mathsf {D}}}\right)}$

La continuité et la dérivabilité de la fonction ${\displaystyle {\bar {G}}}$ aux points B et D induisent qu'à l'équilibre de deux phases les potentiels chimiques d'une espèce chimique dans les deux phases sont égaux^[39] :

${\displaystyle \mu _{1}^{a}\!\left(x_{2}^{\boldsymbol {\mathsf {B}}}\right)=\mu _{1}^{b}\!\left(x_{2}^{\boldsymbol {\mathsf {D}}}\right)}$ ${\displaystyle \mu _{2}^{a}\!\left(x_{2}^{\boldsymbol {\mathsf {B}}}\right)=\mu _{2}^{b}\!\left(x_{2}^{\boldsymbol {\mathsf {D}}}\right)}$

Classification des transitions de phase

Classification d'Ehrenfest

La classification d'Ehrenfest des transitions de phase repose sur le principe suivant^{[42],[43],[44],[45],[46]} :

« Une transition de phase est d'ordre n si la fonction enthalpie libre et ses dérivées jusqu'à l'ordre n-1 sont continues, tandis qu'une de ses dérivées d'ordre n au moins est discontinue. »

La classification d'Ehrenfest est aujourd'hui abandonnée au profit d'une classification qui en reprend partiellement le principe ainsi que d'autres énoncés par Landau. Elle permet néanmoins de définir les principales transitions de phase étudiées en thermodynamique, notamment les changements d'état.

Invariance de l'enthalpie libre^{[43],[44],[45],[46]}

Dans ces conditions, pour toute transition d'une phase ${\displaystyle a}$ à une phase ${\displaystyle b}$, l'enthalpie libre ${\displaystyle G}$ est continue, c'est-à-dire invariante lors de cette transition^[43] :

${\displaystyle G^{b}=G^{a}}$

Ceci revient à l'égalité des potentiels chimiques des deux phases :

${\displaystyle \mu ^{b}={G^{b} \over n}={G^{a} \over n}=\mu ^{a}}$

Transition d'ordre 1^{[43],[44],[45],[46]}

Les dérivées partielles d'ordre 1 de l'enthalpie libre sont^[43] :

${\displaystyle \left({\partial G \over \partial P}\right)_{T}=V}$

${\displaystyle \left({\partial G \over \partial T}\right)_{P}=-S}$

Dans une transition d'ordre 1 les dérivées d'ordre 1 sont discontinues, d'où :

${\displaystyle V^{b}\neq V^{a}}$

${\displaystyle S^{b}\neq S^{a}}$

avec :

• ${\displaystyle V^{a}}$ et ${\displaystyle V^{b}}$ les volumes des phases ${\displaystyle a}$ et ${\displaystyle b}$ ;
• ${\displaystyle S^{a}}$ et ${\displaystyle S^{b}}$ les entropies des phases ${\displaystyle a}$ et ${\displaystyle b}$.

Dans une transition d'ordre 1 le système étudié change de volume. De plus, il y a une entropie de changement d'état ${\displaystyle \Delta _{a\to b}S}$ et donc une enthalpie de changement d'état ${\displaystyle \Delta _{a\to b}H}$ :

${\displaystyle \Delta _{a\to b}S={S^{b}-S^{a} \over n}}$

${\displaystyle \Delta _{a\to b}H=T\,\Delta _{a\to b}S}$

Les transitions d'ordre 1 correspondent aux changements d'état, qui nécessitent un transfert thermique (échange de chaleur) entre la matière étudiée et l'extérieur. Ce type de transition s'effectue par une succession continue d'équilibres des deux phases, l'une disparaissant progressivement au profit de l'autre. Si l'apport de chaleur est interrompu au cours de la transformation, alors celle-ci s'interrompt et les deux phases présentes subsistent sans autre modification^{[10],[42],[47],[44],[45],[46]}.

Par exemple, si l'on place de l'eau liquide dans un récipient fermé pouvant changer de volume et que l'on chauffe à pression atmosphérique, l'eau se met à bouillir à 100 °C et se vaporise progressivement. Si l'on coupe la chauffe au cours de cette transition et que l'on maintient le récipient à pression atmosphérique et 100 °C, alors on observe deux états (vapeur et liquide) coexistant de façon stable tant que l'on ne rétablit pas la chauffe. Lorsque la transition est totalement accomplie, le volume résultant de gaz est bien supérieur au volume initial de liquide.

Une transition de phase d'ordre supérieur s'effectue sans enthalpie de changement d'état. Toutes les transitions de phase sans changement d'état sont donc des transitions de phase d'ordre supérieur à 1^{[10],[42],[47],[44],[46]}.

Transition d'ordre 2^{[43],[44],[45],[46]}

Dans une transition d'ordre 2 les dérivées d'ordre 1 sont continues :

${\displaystyle V^{b}=V^{a}}$

${\displaystyle S^{b}=S^{a}}$

Les dérivées partielles d'ordre 2 de l'enthalpie libre sont ^[43] :

${\displaystyle \left({\partial ^{2}G \over \partial T^{2}}\right)_{P}=-\left({\partial S \over \partial T}\right)_{P}=-{C_{P} \over T}}$

${\displaystyle \left({\partial ^{2}G \over \partial P\partial T}\right)=-\left({\partial S \over \partial P}\right)_{T}=\left({\partial ^{2}G \over \partial T\partial P}\right)=\left({\partial V \over \partial T}\right)_{P}=V\alpha }$

${\displaystyle \left({\partial ^{2}G \over \partial P^{2}}\right)_{T}=\left({\partial V \over \partial P}\right)_{T}=-V\chi _{T}}$

La température ${\displaystyle T}$ et le volume ${\displaystyle V=V^{b}=V^{a}}$ sont communs aux deux phases. Dans une transition d'ordre 2 les dérivées d'ordre 2 sont discontinues, d'où :

${\displaystyle C_{P}^{b}\neq C_{P}^{a}}$

${\displaystyle \alpha ^{b}\neq \alpha ^{a}}$

${\displaystyle \chi _{T}^{b}\neq \chi _{T}^{a}}$

avec :

• ${\displaystyle \alpha ^{a}}$ et ${\displaystyle \alpha ^{b}}$ les coefficients de dilatation isobare des phases ${\displaystyle a}$ et ${\displaystyle b}$ ; ${\displaystyle \alpha ={1 \over V}\left({\partial V \over \partial T}\right)_{P}}$ ;
• ${\displaystyle \chi _{T}^{a}}$ et ${\displaystyle \chi _{T}^{b}}$ les coefficients de compressibilité isotherme des phases ${\displaystyle a}$ et ${\displaystyle b}$ ; ${\displaystyle \chi _{T}=-{1 \over V}\left({\partial V \over \partial P}\right)_{T}}$ ;
• ${\displaystyle C_{P}^{a}}$ et ${\displaystyle C_{P}^{b}}$ les capacités thermiques isobares des phases ${\displaystyle a}$ et ${\displaystyle b}$ ; ${\displaystyle C_{P}=T\left({\partial S \over \partial T}\right)_{P}}$.

Dans une transition de phase d'ordre 2, le corps pur ne change pas de volume, la transformation ne nécessite pas un apport de chaleur et les deux phases ne coexistent pas. Un exemple de transition d'ordre 2 est la transition conducteur-supraconducteur d'un métal^{[43],[42],[46]}. La transition liquide-gaz au point critique est également une transition d'ordre 2^[10],[46].

Transitions d'ordre supérieur^[42]

La condensation de Bose-Einstein d'un gaz parfait formé de bosons est un exemple de transition d'ordre 3. La transition de Kosterlitz-Thouless est un cas extrême de transition d'ordre infini^[42].

Formules de Clapeyron et d'Ehrenfest

Soit une transition de phase d'une phase notée ${\displaystyle a}$ à une autre notée ${\displaystyle b}$ s'effectuant à la température ${\displaystyle T}$ donnée et à la pression constante ${\displaystyle P_{a\to b}}$. La variation de la pression ${\displaystyle P_{a\to b}}$ en fonction de la température ${\displaystyle T}$ peut être déterminée théoriquement. Les formules suivantes donnent les pentes des courbes délimitant les domaines représentés dans les diagrammes de phases représentant la pression en fonction de la température.

Pour un changement d'état (une transition de phase d'ordre 1 selon la classification d'Ehrenfest^[42] des transitions de phase), la pression de changement d'état ${\displaystyle P_{a\to b}}$ d'un corps pur varie en fonction de la température ${\displaystyle T}$ selon la formule de Clapeyron^[48],[47] :

Formule de Clapeyron : ${\displaystyle \left({\mathrm {d} P_{a\to b} \over \mathrm {d} T}\right)={\Delta _{a\to b}H \over T\cdot \left({\bar {V}}^{b}-{\bar {V}}^{a}\right)}}$ pour un corps pur.

La formule de Clapeyron étendue aux mélanges, pour un mélange de ${\displaystyle N}$ constituants notés ${\displaystyle i}$, pour une phase ${\displaystyle a}$ de composition constante ${\displaystyle x^{a}}$ en équilibre avec une phase ${\displaystyle b}$ de composition variable ${\displaystyle x^{b}}$, s'écrit^{[49],[50],[51]} :

Formule de Clapeyron étendue aux mélanges : ${\displaystyle \left({\partial P_{a\to b} \over \partial T}\right)_{x^{a}}={{\bar {H}}^{b}-\sum _{i=1}^{N}x_{i}^{b}\,{\bar {H}}_{i}^{a} \over T\cdot \left({\bar {V}}^{b}-\sum _{i=1}^{N}x_{i}^{b}\,{\bar {V}}_{i}^{a}\right)}}$

Pour une transition de phase d'ordre 2 selon la classification d'Ehrenfest, la pression de transition de phase ${\displaystyle P_{a\to b}}$ varie en fonction de la température ${\displaystyle T}$ selon les formules d'Ehrenfest^[42],[47] :

Formules d'Ehrenfest : ${\displaystyle \left({\mathrm {d} P_{a\to b} \over \mathrm {d} T}\right)={\alpha ^{b}-\alpha ^{a} \over \chi _{T}^{b}-\chi _{T}^{a}}}$ ${\displaystyle \left({\mathrm {d} P_{a\to b} \over \mathrm {d} T}\right)={{\bar {C}}_{P}^{b}-{\bar {C}}_{P}^{a} \over T{\bar {V}}\cdot \left(\alpha ^{b}-\alpha ^{a}\right)}}$

avec :

Calcul d'un équilibre liquide-vapeur

Le calcul d'équilibre liquide-vapeur est le plus documenté dans la littérature. Son principe peut être décliné à tout autre équilibre de phases, notamment aux équilibres vapeur-liquide-liquide et vapeur-liquide-solide.

Énoncé du problème

Mise en équations

Soit, à pression ${\displaystyle P}$ et température ${\displaystyle T}$ données, un mélange de ${\displaystyle N}$ constituants, chaque constituant ${\displaystyle i}$ étant représenté par la quantité de matière ${\displaystyle n_{i}}$. On cherche à déterminer la composition des phases liquide et vapeur en présence. Il s'agit de calculer pour chacun des ${\displaystyle N}$ constituants :

• ${\displaystyle n_{i}^{\text{g}}}$ la quantité du constituant ${\displaystyle i}$ en phase vapeur ;
• ${\displaystyle n_{i}^{\text{l}}}$ la quantité du constituant ${\displaystyle i}$ en phase liquide ;

qui doivent répondre aux équations :

• ${\displaystyle n_{i}=n_{i}^{\text{l}}+n_{i}^{\text{g}}}$ du bilan de matière ;
• ${\displaystyle f_{i}^{\text{g}}=f_{i}^{\text{l}}}$ de l'équilibre liquide-vapeur.

On a donc ${\displaystyle 2\cdot N}$ inconnues et ${\displaystyle 2\cdot N}$ équations.

Reformulation

On définit les variables intermédiaires :

• ${\displaystyle n^{\text{g}}=\sum _{i=1}^{N}n_{i}^{\text{g}}}$ la quantité de matière totale en phase vapeur ;
• ${\displaystyle n^{\text{l}}=\sum _{i=1}^{N}n_{i}^{\text{l}}}$ la quantité de matière totale en phase liquide ;
• ${\displaystyle n=\sum _{i=1}^{N}n_{i}}$ la quantité de matière totale considérée ;
• ${\displaystyle x_{i}^{\text{g}}={n_{i}^{\text{g}} \over n^{\text{g}}}}$ la fraction molaire du constituant ${\displaystyle i}$ en phase vapeur ;
• ${\displaystyle x_{i}^{\text{l}}={n_{i}^{\text{l}} \over n^{\text{l}}}}$ la fraction molaire du constituant ${\displaystyle i}$ en phase liquide.

Soit pour chacun des ${\displaystyle N}$ constituants la fraction molaire globale, notée ${\displaystyle x_{i}}$ :

Fraction molaire globale du corps ${\displaystyle i}$ : ${\displaystyle x_{i}={n_{i} \over n}}$

On définit enfin ${\displaystyle \tau ^{\text{g}}}$ la fraction molaire globale de la phase vapeur, ou taux de vaporisation (inconnue) :

Taux de vaporisation ou fraction de vapeur : ${\displaystyle \tau ^{\text{g}}={n^{\text{g}} \over n^{\text{g}}+n^{\text{l}}}}$

Les fractions ${\displaystyle x_{i}}$ sont calculées directement à partir des données du problème. Les variables ${\displaystyle n_{i}^{\text{g}}}$, ${\displaystyle n^{\text{g}}}$, ${\displaystyle x_{i}^{\text{g}}}$, ${\displaystyle n_{i}^{\text{l}}}$, ${\displaystyle n^{\text{l}}}$, ${\displaystyle x_{i}^{\text{l}}}$ et ${\displaystyle \tau ^{\text{g}}}$ sont des inconnues. Le problème est reformulé de façon à n'avoir à déterminer que les fractions ${\displaystyle x_{i}^{\text{g}}}$ et ${\displaystyle x_{i}^{\text{l}}}$, et le taux de vaporisation ${\displaystyle \tau ^{\text{g}}}$, soit ${\displaystyle 2\cdot N+1}$ inconnues. Les ${\displaystyle 2\cdot N+1}$ équations résolues sont^[52],[53] :

• les ${\displaystyle N}$ bilans de matière ${\displaystyle x_{i}=x_{i}^{\text{l}}\left(1-\tau ^{\text{g}}\right)+x_{i}^{\text{g}}\tau ^{\text{g}}}$, reformulés selon les fractions molaires ;
• les ${\displaystyle N}$ équilibres ${\displaystyle x_{i}^{\text{g}}=K_{i}x_{i}^{\text{l}}}$, reformulés à l'aide des coefficients de partage ;
• la contrainte ${\displaystyle \sum _{i=1}^{N}x_{i}^{\text{g}}-\sum _{i=1}^{N}x_{i}^{\text{l}}=0}$.

Les quantités des phases et des constituants peuvent être déduites à postériori selon :

${\displaystyle n^{\text{g}}=\tau ^{\text{g}}n}$

${\displaystyle n^{\text{l}}=\left(1-\tau ^{\text{g}}\right)n}$

${\displaystyle n_{i}^{\text{g}}=x_{i}^{\text{g}}n^{\text{g}}}$

${\displaystyle n_{i}^{\text{l}}=x_{i}^{\text{l}}n^{\text{l}}}$

Fugacités et coefficient de partage

Les fugacités sont des fonctions de la pression ${\displaystyle P}$ et de la température ${\displaystyle T}$ du mélange à l'équilibre, et de la composition ${\displaystyle x_{i}}$ de la phase considérée :

${\displaystyle f_{i}^{\text{g}}=f_{i}^{\text{g}}\!\left(P,T,x_{1}^{\text{g}},\cdots ,x_{N}^{\text{g}}\right)}$

${\displaystyle f_{i}^{\text{l}}=f_{i}^{\text{l}}\!\left(P,T,x_{1}^{\text{l}},\cdots ,x_{N}^{\text{l}}\right)}$

Les fugacités sont le plus souvent calculées selon deux approches : celle par coefficient de fugacité ${\displaystyle \phi _{i}}$, nécessitant une équation d'état, et celle par coefficient d'activité ${\displaystyle \gamma _{i}}$, nécessitant un modèle de coefficient d'activité. Ces deux approches sont en théorie équivalentes, mais en pratique leur usage dépend de la pression considérée. L'approche par coefficient de fugacité est employée à toutes les pressions pour la phase gaz et à des pressions supérieures à 10 bar pour la phase liquide. L'usage d'une même équation d'état pour représenter les deux phases (par exemple une équation d'état cubique comme celle de van der Waals) rend le calcul cohérent à l'approche du point critique, où les deux phases doivent se rejoindre^[54]. Par contre, aux basses pressions, les équations d'état, spécialement développées pour les gaz, représentent souvent assez mal les liquides. Les modèles de coefficient d'activité sont spécialement développés pour les liquides aux basses pressions (par exemple les modèles de Margules, UNIQUAC, UNIFAC, COSMOSPACE). Ils ne dépendent généralement pas de la pression, mais seulement de la température et de la composition.

L'approche par coefficient de fugacité ${\displaystyle \phi _{i}}$ donne^[55],[54] :

Pour les espèces en phase gaz : ${\displaystyle f_{i}^{\text{g}}=x_{i}^{\text{g}}\phi _{i}^{\text{g}}P}$ quelle que soit la pression. Pour les espèces en phase liquide : ${\displaystyle f_{i}^{\text{l}}=x_{i}^{\text{l}}\phi _{i}^{\text{l}}P}$ aux hautes pressions.

L'approche par coefficient d'activité ${\displaystyle \gamma _{i}}$ donne :

Pour les espèces en phase liquide : ${\displaystyle f_{i}^{\text{l}}=x_{i}^{\text{l}}\gamma _{i}^{\text{l}}f_{i}^{{\text{l}},*}}$ aux basses pressions.

Cette approche nécessite de connaitre la fugacité ${\displaystyle f_{i}^{{\text{l}},*}}$ de l'espèce chimique ${\displaystyle i}$ à l'état de corps pur liquide dans les conditions de pression ${\displaystyle P}$ et température ${\displaystyle T}$ du mélange à l'équilibre.

Pour une espèce liquide dans les conditions du mélange, pour laquelle il existe une pression de vapeur saturante ${\displaystyle P_{i}^{\text{sat}}}$ à la température ${\displaystyle T}$ telle que ${\displaystyle P>P_{i}^{\text{sat}}}$, cette fugacité se calcule selon :

Pour les espèces liquides : ${\displaystyle f_{i}^{{\text{l}},*}=\phi _{i}^{\text{g,*,sat}}P_{i}^{\text{sat}}{\mathcal {P}}_{i}}$

avec :

• ${\displaystyle P_{i}^{\text{sat}}}$ la pression de vapeur saturante du corps ${\displaystyle i}$ pur à ${\displaystyle T}$ ;
• ${\displaystyle \phi _{i}^{\text{g,*,sat}}}$ le coefficient de fugacité du corps ${\displaystyle i}$ pur à saturation en phase vapeur, à ${\displaystyle P_{i}^{\text{sat}}}$ et ${\displaystyle T}$ ;
• ${\displaystyle {\bar {V}}_{i}^{{\text{l}},*}}$ le volume molaire liquide du corps ${\displaystyle i}$ pur à ${\displaystyle T}$ ; dépend également de la pression ;
• ${\displaystyle {\mathcal {P}}_{i}=\exp \!\left({\int _{P_{i}^{\text{sat}}}^{P}{\bar {V}}_{i}^{{\text{l}},*}\,\mathrm {d} P \over RT}\right)}$ la correction de Poynting.

Pour une espèce supercritique dans les conditions du mélange, pour laquelle il n'existe pas de pression de vapeur saturante à la température du mélange (c'est-à-dire ${\displaystyle T>T_{{\text{c}},i}}$, la température critique de l'espèce), ou gazeuse, pour laquelle il existe une pression de vapeur saturante telle que ${\displaystyle P<P_{i}^{\text{sat}}}$, la fugacité ${\displaystyle f_{i}^{{\text{l}},*}}$ est fictive et peut être calculée par extrapolation à l'aide d'une constante de Henry ${\displaystyle k_{{\text{H}},i}^{\text{l}}}$ (déterminée expérimentalement) selon la relation^[56] :

Pour les espèces supercritiques ou gazeuses : ${\displaystyle f_{i}^{{\text{l}},*}={k_{{\text{H}},i}^{\text{l}} \over \gamma _{i}^{{\text{l}},\infty }}}$

avec le coefficient d'activité à dilution infinie^[56] :

${\displaystyle \gamma _{i}^{{\text{l}},\infty }=\lim _{x_{i}^{\text{l}}\to 0}\gamma _{i}^{\text{l}}}$

Les approches par coefficient de fugacité et par coefficient d'activité étant théoriquement équivalentes à toutes les pressions, on a, pour les approches aux basses pressions :

${\displaystyle \phi _{i}^{\text{l}}=\gamma _{i}^{\text{l}}{f_{i}^{{\text{l}},*} \over P}}$

Pour tout corps ${\displaystyle i}$, quelle que soit la pression, on définit le coefficient de partage ${\displaystyle K_{i}}$ à partir de l'égalité des fugacités^[54] ${\displaystyle f_{i}^{\text{g}}=x_{i}^{\text{g}}\phi _{i}^{\text{g}}P=f_{i}^{\text{l}}=x_{i}^{\text{l}}\phi _{i}^{\text{l}}P}$ :

Coefficient de partage : ${\displaystyle K_{i}={x_{i}^{\text{g}} \over x_{i}^{\text{l}}}={\phi _{i}^{\text{l}} \over \phi _{i}^{\text{g}}}}$

Les coefficients de partage ${\displaystyle K_{i}}$ sont des inconnues, ils dépendent de la pression, de la température et des compositions des deux phases :

${\displaystyle K_{i}=K_{i}\!\left(P,T,x_{1}^{\text{g}},\cdots ,x_{N}^{\text{g}},x_{1}^{\text{l}},\cdots ,x_{N}^{\text{l}}\right)}$

Dans le système d'équations décrivant l'équilibre de phases, les égalités des fugacités ${\displaystyle f_{i}^{\text{g}}=f_{i}^{\text{l}}}$ sont remplacées par les équations équivalentes ${\displaystyle x_{i}^{\text{g}}=K_{i}x_{i}^{\text{l}}}$.

Calcul d'un point de bulle

Un point de bulle est un couple de pression et température auquel apparait la première bulle de vapeur dans un liquide lors d'une vaporisation.

Calcul de la pression de bulle

Dans ce cas, la température ${\displaystyle T}$ est connue et le mélange est entièrement liquide, soit ${\displaystyle \tau ^{\text{g}}=0}$. Le problème consiste à déterminer la pression ${\displaystyle P}$ à laquelle apparait la première bulle de gaz et la composition de celui-ci, les fractions ${\displaystyle x_{i}^{\text{g}}}$, soit ${\displaystyle N+1}$ inconnues. On a directement :

${\displaystyle n^{\text{l}}=n}$

${\displaystyle n^{\text{g}}=0}$

${\displaystyle x_{i}^{\text{l}}=x_{i}}$

${\displaystyle n_{i}^{\text{l}}=n_{i}}$

${\displaystyle n_{i}^{\text{g}}=0}$

Les ${\displaystyle N+1}$ équations sont^[57] :

• les ${\displaystyle N}$ équilibres ${\displaystyle x_{i}^{\text{g}}=K_{i}x_{i}^{\text{l}}}$ ;
• la contrainte ${\displaystyle \sum _{i=1}^{N}x_{i}^{\text{g}}=1}$.

L'intégration des équilibres dans la contrainte donne l'équation à résoudre^[57] :

Équation du point de bulle : ${\displaystyle \sum _{i=1}^{N}K_{i}x_{i}=1}$

L'égalité des fugacités ${\displaystyle f_{i}^{\text{g}}=f_{i}^{\text{l}}}$ donne ${\displaystyle x_{i}^{\text{g}}\phi _{i}^{\text{g}}P=x_{i}^{\text{l}}\phi _{i}^{\text{l}}P}$, d'où ${\displaystyle x_{i}^{\text{g}}P=K_{i}x_{i}^{\text{l}}P=K_{i}x_{i}P}$ et, par sommation sur les ${\displaystyle N}$ constituants :

${\displaystyle \left(\sum _{i=1}^{N}x_{i}^{\text{g}}\right)P=P=\left(\sum _{i=1}^{N}K_{i}x_{i}\right)P}$

Cette équation peut être utilisée pour résoudre le problème par la méthode itérative du point fixe. Connaissant la pression ${\displaystyle P_{k}}$ à l'itération ${\displaystyle k}$, la pression ${\displaystyle P_{k+1}}$ à l'itération ${\displaystyle k+1}$ est calculée selon :

${\displaystyle P_{k+1}=\left(\sum _{i=1}^{N}K_{i}x_{i}\right)_{k}P_{k}}$

À chaque itération, on calcule la somme :

${\displaystyle \Sigma ^{\text{g}}=\sum _{i=1}^{N}K_{i}x_{i}}$

Cette somme est censée valoir ${\displaystyle \Sigma ^{\text{g}}=\sum _{i=1}^{N}x_{i}^{\text{g}}=1}$, ce qui n'est vrai que lorsque le calcul a convergé. Pour pouvoir calculer les coefficients ${\displaystyle K_{i}}$, il est nécessaire de normer les fractions molaires au cours des itérations selon^[57] :

${\displaystyle {\tilde {x}}_{i}^{\text{g}}={K_{i}x_{i} \over \Sigma ^{\text{g}}}}$

Lorsque ${\displaystyle \Sigma ^{\text{g}}=1}$, on a bien ${\displaystyle {\tilde {x}}_{i}^{\text{g}}=x_{i}^{\text{g}}}$.

Le calcul est initialisé par le choix d'une pression ${\displaystyle P}$ et de fractions molaires ${\displaystyle x_{i}^{\text{g}}}$, et peut être effectué selon l'algorithme suivant (${\displaystyle k}$ est l'itération en cours)^[57].

Algorithme de calcul de la pression de bulle

1. Calculer les coefficients de partage ${\displaystyle K_{i}}$ par les coefficients de fugacité et d'activité.
2. Calculer la somme ${\displaystyle \Sigma ^{\text{g}}}$.
3. Calculer les fractions molaires normées ${\displaystyle {\tilde {x}}_{i}^{\text{g}}}$.
4. Calculer une nouvelle pression ${\displaystyle P_{k+1}=\Sigma ^{\text{g}}P_{k}}$.
5. Si la valeur absolue ${\displaystyle |P_{k+1}-P_{k}|>\epsilon }$, une erreur acceptable, recommencer en 1 avec la nouvelle pression. Sinon, la pression de bulle est trouvée. FIN.

Calcul de la température de bulle

Dans ce cas, la pression ${\displaystyle P}$ est connue. Le problème consiste à déterminer la température ${\displaystyle T}$ à laquelle apparait la première bulle de gaz et la composition de celui-ci, soit les ${\displaystyle N}$ fractions ${\displaystyle x_{i}^{\text{g}}}$. Les équations sont les mêmes que pour le calcul de la pression de bulle. On peut effectuer le calcul en faisant une hypothèse de température, en calculant la pression de bulle correspondante selon l'algorithme exposé dans la section précédente, puis en modifiant la température jusqu'à ce que la pression calculée corresponde à la pression ${\displaystyle P}$ donnée^[57].

Calcul d'un point de rosée

Un point de rosée est un couple de pression et température auquel apparait la première goutte de liquide dans un gaz lors d'une liquéfaction.

Calcul de la pression de rosée

Dans ce cas, la température ${\displaystyle T}$ est connue et le mélange est entièrement gazeux, soit ${\displaystyle \tau ^{\text{g}}=1}$. Le problème consiste à déterminer la pression ${\displaystyle P}$ à laquelle apparait la première goutte de liquide et la composition de celui-ci, les fractions ${\displaystyle x_{i}^{\text{l}}}$, soit ${\displaystyle N+1}$ inconnues. On a directement :

${\displaystyle n^{\text{g}}=n}$

${\displaystyle n^{\text{l}}=0}$

${\displaystyle x_{i}^{\text{g}}=x_{i}}$

${\displaystyle n_{i}^{\text{g}}=n_{i}}$

${\displaystyle n_{i}^{\text{l}}=0}$

Les ${\displaystyle N+1}$ équations sont^[58] :

• les ${\displaystyle N}$ équilibres ${\displaystyle x_{i}^{\text{g}}=K_{i}x_{i}^{\text{l}}}$ ;
• la contrainte ${\displaystyle \sum _{i=1}^{N}x_{i}^{\text{l}}=1}$.

L'intégration des équilibres dans la contrainte donne l'équation à résoudre^[58] :

Équation du point de rosée : ${\displaystyle \sum _{i=1}^{N}{x_{i} \over K_{i}}=1}$

L'égalité des fugacités ${\displaystyle f_{i}^{\text{g}}=f_{i}^{\text{l}}}$ donne ${\displaystyle x_{i}^{\text{g}}\phi _{i}^{\text{g}}P=x_{i}^{\text{l}}\phi _{i}^{\text{l}}P}$, d'où ${\displaystyle {x_{i}^{\text{g}} \over K_{i}}P={x_{i} \over K_{i}}P=x_{i}^{\text{l}}P}$ et, par sommation sur les ${\displaystyle N}$ constituants :

${\displaystyle \left(\sum _{i=1}^{N}{x_{i} \over K_{i}}\right)P=\left(\sum _{i=1}^{N}x_{i}^{\text{l}}\right)P=P}$

Cette équation peut être utilisée pour résoudre le problème par la méthode itérative du point fixe. Connaissant la pression ${\displaystyle P_{k}}$ à l'itération ${\displaystyle k}$, la pression ${\displaystyle P_{k+1}}$ à l'itération ${\displaystyle k+1}$ est calculée selon :

${\displaystyle P_{k+1}=\left(\sum _{i=1}^{N}{x_{i} \over K_{i}}\right)_{k}P_{k}}$

À chaque itération, on calcule la somme :

${\displaystyle \Sigma ^{\text{l}}=\sum _{i=1}^{N}{x_{i} \over K_{i}}}$

Cette somme est censée valoir ${\displaystyle \Sigma ^{\text{l}}=\sum _{i=1}^{N}x_{i}^{\text{l}}=1}$, ce qui n'est vrai que lorsque le calcul a convergé. Pour pouvoir calculer les coefficients ${\displaystyle K_{i}}$, il est nécessaire de normer les fractions molaires au cours des itérations selon^[58] :

${\displaystyle {\tilde {x}}_{i}^{\text{l}}={x_{i} \over K_{i}\Sigma ^{\text{l}}}}$

Lorsque ${\displaystyle \Sigma ^{\text{l}}=1}$, on a bien ${\displaystyle {\tilde {x}}_{i}^{\text{l}}=x_{i}^{\text{l}}}$.

Le calcul est initialisé par le choix d'une pression ${\displaystyle P}$ et de fractions molaires ${\displaystyle x_{i}^{\text{l}}}$, et peut être effectué selon l'algorithme suivant (${\displaystyle k}$ est l'itération en cours)^[58].

Algorithme de calcul de la pression de rosée

1. Calculer les coefficients de partage ${\displaystyle K_{i}}$ par les coefficients de fugacité et d'activité.
2. Calculer la somme ${\displaystyle \Sigma ^{\text{l}}}$.
3. Calculer les fractions molaires normées ${\displaystyle {\tilde {x}}_{i}^{\text{l}}}$.
4. Calculer une nouvelle pression ${\displaystyle P_{k+1}=\Sigma ^{\text{l}}P_{k}}$.
5. Si la valeur absolue ${\displaystyle |P_{k+1}-P_{k}|>\epsilon }$, une erreur acceptable, recommencer en 1 avec la nouvelle pression. Sinon, la pression de rosée est trouvée. FIN.

Calcul de la température de rosée

Dans ce cas, la pression ${\displaystyle P}$ est connue. Le problème consiste à déterminer la température ${\displaystyle T}$ à laquelle apparait la première goutte de liquide et la composition de celui-ci, soit les ${\displaystyle N}$ fractions ${\displaystyle x_{i}^{\text{l}}}$. Les équations sont les mêmes que pour le calcul de la pression de rosée. On peut effectuer le calcul en faisant une hypothèse de température, en calculant la pression de rosée correspondante selon l'algorithme exposé dans la section précédente, puis en modifiant la température jusqu'à ce que la pression calculée corresponde à la pression ${\displaystyle P}$ donnée^[58].

Calcul pour une vaporisation partielle

On connait la pression ${\displaystyle P}$, la température ${\displaystyle T}$ et les fractions molaires globales ${\displaystyle x_{i}}$. Le taux de vaporisation ${\displaystyle \tau ^{\text{g}}}$ et les fractions dans les phases ${\displaystyle x_{i}^{\text{g}}}$ et ${\displaystyle x_{i}^{\text{l}}}$ sont inconnues, soit ${\displaystyle 2\cdot N+1}$ inconnues.

En substituant l'équilibre dans le bilan de matière de chacun des ${\displaystyle N}$ constituants, on obtient :

${\displaystyle x_{i}=x_{i}^{\text{l}}\left(1-\tau ^{\text{g}}\right)+x_{i}^{\text{g}}\tau ^{\text{g}}=\left(1+\left(K_{i}-1\right)\tau ^{\text{g}}\right)x_{i}^{\text{l}}}$

Si ${\displaystyle 1+\left(K_{i}-1\right)\tau ^{\text{g}}=0}$, alors ${\displaystyle x_{i}=0}$ : le constituant ${\displaystyle i}$ n'est pas présent dans le mélange ; ce cas est donc exclu. On obtient ${\displaystyle 2\cdot N}$ équations combinant les bilans de matière et les équilibres^[52] :

• ${\displaystyle x_{i}^{\text{l}}={x_{i} \over 1+\left(K_{i}-1\right)\tau ^{\text{g}}}}$ ;
• ${\displaystyle x_{i}^{\text{g}}={K_{i}x_{i} \over 1+\left(K_{i}-1\right)\tau ^{\text{g}}}}$.

Les contraintes combinées sur les fractions molaires ${\displaystyle x_{i}^{\text{g}}}$ et ${\displaystyle x_{i}^{\text{l}}}$ donnent la dernière équation :

${\displaystyle \sum _{i=1}^{N}x_{i}^{\text{g}}-\sum _{i=1}^{N}x_{i}^{\text{l}}=\sum _{i=1}^{N}{\left(K_{i}-1\right)x_{i} \over 1+\left(K_{i}-1\right)\tau ^{\text{g}}}=0}$

Le problème est réduit à trouver la solution de cette équation, due à Rachford et Rice (1952)^{[59],[60],[61],[52]} :

Équation de Rachford-Rice : ${\displaystyle f\!\left(\tau ^{\text{g}}\right)=\sum _{i=1}^{N}{\left(K_{i}-1\right)x_{i} \over 1+\left(K_{i}-1\right)\tau ^{\text{g}}}=0}$

La dérivée ${\displaystyle f'}$ de cette fonction s'écrit :

${\displaystyle f'\!\left(\tau ^{\text{g}}\right)=-\sum _{i=1}^{N}{\left(K_{i}-1\right)^{2}x_{i} \over \left(1+\left(K_{i}-1\right)\tau ^{\text{g}}\right)^{2}}}$

On a ${\displaystyle f'\!\left(\tau ^{\text{g}}\right)<0}$ : cette fonction est monotone strictement décroissante en ${\displaystyle \tau ^{\text{g}}}$. Si l'on trouve sur la plage ${\displaystyle 0<\tau ^{\text{g}}<1}$ une solution de l'équation ${\displaystyle f\!\left(\tau ^{\text{g}}\right)=0}$, cette solution est unique.

On peut résoudre l'équation de Rachford-Rice sur l'intervalle ${\displaystyle 0\leq \tau ^{\text{g}}\leq 1}$ par la méthode de Newton selon (${\displaystyle j}$ est l'itération en cours)^[52] :

${\displaystyle \tau _{j+1}^{\text{g}}=\tau _{j}^{\text{g}}-{f\!\left(\tau _{j}^{\text{g}}\right) \over f'\!\left(\tau _{j}^{\text{g}}\right)}}$

La méthode de dichotomie peut également être employée^[60].

À chaque itération les sommes suivantes sont calculées :

${\displaystyle \Sigma ^{\text{g}}=\sum _{i=1}^{N}{K_{i}x_{i} \over 1+\left(K_{i}-1\right)\tau ^{\text{g}}}}$

${\displaystyle \Sigma ^{\text{l}}=\sum _{i=1}^{N}{x_{i} \over 1+\left(K_{i}-1\right)\tau ^{\text{g}}}}$

Ces sommes sont censées valoir ${\displaystyle \Sigma ^{\text{g}}=\sum _{i=1}^{N}x_{i}^{\text{g}}=1}$ et ${\displaystyle \Sigma ^{\text{l}}=\sum _{i=1}^{N}x_{i}^{\text{l}}=1}$, ce qui n'est vrai que lorsque le calcul a convergé. Pour pouvoir calculer les coefficients ${\displaystyle K_{i}}$, il est nécessaire de normer les fractions molaires au cours des itérations selon :

${\displaystyle {\tilde {x}}_{i}^{\text{g}}={K_{i}x_{i} \over \left(1+\left(K_{i}-1\right)\tau ^{\text{g}}\right)\cdot \Sigma ^{\text{g}}}}$

${\displaystyle {\tilde {x}}_{i}^{\text{l}}={x_{i} \over \left(1+\left(K_{i}-1\right)\tau ^{\text{g}}\right)\cdot \Sigma ^{\text{l}}}}$

Lorsque ${\displaystyle \Sigma ^{\text{g}}=\Sigma ^{\text{l}}=1}$, on a bien ${\displaystyle {\tilde {x}}_{i}^{\text{g}}=x_{i}^{\text{g}}}$, ${\displaystyle {\tilde {x}}_{i}^{\text{l}}=x_{i}^{\text{l}}}$ et ${\displaystyle f\left(\tau ^{\text{g}}\right)=\Sigma ^{\text{g}}-\Sigma ^{\text{l}}=0}$.

Le calcul est initialisé par le choix d'un taux de vaporisation ${\displaystyle 0<\tau ^{\text{g}}<1}$, de fractions molaires ${\displaystyle x_{i}^{\text{g}}}$ et ${\displaystyle x_{i}^{\text{l}}}$, et de coefficients de partage ${\displaystyle K_{i}}$. L'algorithme de résolution comporte deux boucles imbriquées^[52],[60] : une sur les coefficients ${\displaystyle K_{i}}$, l'autre sur ${\displaystyle \tau ^{\text{g}}}$.

Algorithme de calcul d'une vaporisation partielle

1. Calculer les sommes ${\displaystyle \Sigma ^{\text{g}}}$ et ${\displaystyle \Sigma ^{\text{l}}}$.
2. Calculer les fractions molaires normées ${\displaystyle {\tilde {x}}_{i}^{\text{g}}}$ et ${\displaystyle {\tilde {x}}_{i}^{\text{l}}}$.
3. Calculer les coefficients de partage ${\displaystyle K_{i}}$ par les coefficients de fugacité et d'activité.
4. Si les équilibres ne sont pas vérifiés (${\displaystyle |{\tilde {x}}_{i}^{\text{g}}-K_{i}{\tilde {x}}_{i}^{\text{l}}|>\epsilon }$ pour au moins un constituant), reprendre en 1 avec les nouvelles fractions et les nouveaux coefficients de partage. Sinon, passer en 5.
5. Résoudre l'équation de Rachford-Rice en ${\displaystyle \tau ^{\text{g}}}$. On obtient ${\displaystyle \tau _{k+1}^{\text{g}}}$ (${\displaystyle k}$ est l'itération en cours).
6. Si ${\displaystyle |\tau _{k+1}^{\text{g}}-\tau _{k}^{\text{g}}|>\epsilon }$, alors reprendre en 1 avec le nouveau taux. Sinon, FIN.

Notes

• Le passage de l'étape 4 à l'étape 5 s'effectue même si ${\displaystyle \Sigma ^{\text{g}}\neq 1}$ ou ${\displaystyle \Sigma ^{\text{l}}\neq 1}$.
• À l'issue du calcul, si ${\displaystyle \tau ^{\text{g}}\geq 1}$, le mélange est entièrement gazeux ; si ${\displaystyle \tau ^{\text{g}}\leq 0}$, le mélange est entièrement liquide. Des calculs préalables de pression de bulle et de rosée peuvent être effectués afin de vérifier ces possibilités et éviter de résoudre le problème de vaporisation partielle.

Équilibres idéaux

Solution idéale

Le terme solution est pris au sens large de mélange. La notion de solution idéale s'applique à toutes les phases, quel que soit leur état. Dans une solution idéale, la fugacité idéale ${\displaystyle f_{i}^{\text{id}}}$ est supposée évoluer, à pression et température données, selon la relation^[64] :

Solution idéale : ${\displaystyle {f_{i}^{\text{id}} \over x_{i}}={f_{i}^{\circ } \over x_{i}^{\circ }}}$

dans laquelle :

• ${\displaystyle f_{i}^{\text{id}}}$ est la fugacité idéale à la fraction molaire ${\displaystyle x_{i}}$ ;
• ${\displaystyle f_{i}^{\circ }}$ est la fugacité à la fraction molaire de référence ${\displaystyle x_{i}^{\circ }}$ (fixe).

Les deux fugacités sont prises aux mêmes pression et température, et pour la même phase. À pression et température données, la fugacité ${\displaystyle f_{i}^{\circ }}$ est une constante, et la fugacité ${\displaystyle f_{i}^{\text{id}}}$ varie linéairement en fonction de ${\displaystyle x_{i}}$. Les fugacités sont parfois exprimées en fonction de la fraction massique, de la concentration molaire ou de la concentration massique.

Dans les modèles idéaux, les coefficients de fugacité ${\displaystyle \phi _{i}}$ et d'activité ${\displaystyle \gamma _{i}}$ sont égaux à 1. Pour un gaz, la solution idéale est le mélange de gaz parfaits. Pour les espèces chimiques en phase liquide, plusieurs états de référence sont souvent employés : le corps pur (${\displaystyle x_{i}^{\circ }=1}$), le corps infiniment dilué (${\displaystyle x_{i}^{\circ }=0}$), le corps à une concentration molaire de 1 mol/l. Pour les espèces chimiques en phase solide, l'état de référence est le plus souvent le corps pur.

Équilibres liquide-vapeur idéaux

Loi de Raoult et loi de Henry

Pour un équilibre liquide-vapeur, l'égalité des fugacités s'écrit :

Équilibre liquide-vapeur : ${\displaystyle f_{i}^{\text{g}}=f_{i}^{\text{l}}}$

Pour la phase gazeuse, le modèle idéal est celui du gaz parfait. La fugacité de tout corps ${\displaystyle i}$ est égale à la pression partielle de ce corps :

${\displaystyle f_{i}^{\text{g}}=f_{i}^{\bullet }=x_{i}^{\text{g}}P}$

Pour un corps ${\displaystyle i}$ en phase liquide, lorsque l'état de référence choisi est celui du corps pur, ${\displaystyle x_{i}^{{\text{l}},\circ }=1}$, alors ${\displaystyle f_{i}^{{\text{l}},\circ }=f_{i}^{{\text{l}},*}}$ est la fugacité du corps pur liquide. La fugacité suit la loi de Lewis et Randall : ${\displaystyle f_{i}^{\text{l}}=x_{i}^{\text{l}}f_{i}^{{\text{l}},*}}$. La fugacité du corps pur liquide se calcule de façon générale selon (voir la section Fugacités et coefficient de partage) :

${\displaystyle f_{i}^{{\text{l}},*}=\phi _{i}^{\text{g,*,sat}}\,P_{i}^{\text{sat}}\,{\mathcal {P}}_{i}^{\text{l}}}$

Dans les équilibres idéaux ${\displaystyle \phi _{i}^{\text{g,*,sat}}=1}$, et aux basses pressions ${\displaystyle {\mathcal {P}}_{i}^{\text{l}}\approx 1}$. On obtient la loi de Raoult^[63] :

Loi de Raoult : ${\displaystyle x_{i}^{\text{g}}P=x_{i}^{\text{l}}P_{i}^{\text{sat}}}$

Pour un corps ${\displaystyle i}$ en phase liquide, lorsque l'état de référence choisi est celui du corps à dilution infinie, ${\displaystyle x_{i}^{{\text{l}},\circ }=0}$, alors ${\displaystyle f_{i}^{{\text{l}},\circ }=0}$ et ${\displaystyle {f_{i}^{{\text{l}},\circ } \over x_{i}^{{\text{l}},\circ }}=k_{{\text{H}},i}}$ la constante de Henry. On obtient la loi de Henry^[63] :

Loi de Henry : ${\displaystyle x_{i}^{\text{g}}P=x_{i}^{\text{l}}k_{{\text{H}},i}}$

Les lois de Raoult et de Henry considèrent toutes deux la phase gaz comme un mélange de gaz parfaits, ce qui restreint leur domaine d'application à des pressions de moins de 10 atm. La loi de Raoult s'applique pour des fractions molaires en phase liquide plutôt grandes, ${\displaystyle x_{i}^{\text{l}}\approx 1}$, et la loi de Henry pour des fractions molaires plutôt petites^[65], ${\displaystyle x_{i}^{\text{l}}\approx 0}$.

Exemple de calcul d'un équilibre idéal

On considère un équilibre liquide-vapeur dont tous les constituants suivent la loi de Raoult. Les données du problème sont la pression ${\displaystyle P}$, la température ${\displaystyle T}$ et les fractions molaires globales ${\displaystyle x_{i}}$. À température donnée, le coefficient de partage de chacun des ${\displaystyle N}$ constituants est une fonction de la pression et ne dépend pas de la composition :

${\displaystyle K_{i}\!\left(P\right)={P_{i}^{\text{sat}}{\mathcal {P}}_{i}^{\text{l}}\!\left(P\right) \over P}}$

Les coefficients de partage sont donc invariants au cours d'un calcul par itérations^[66].

Avant de calculer un équilibre liquide-vapeur, il est nécessaire de vérifier que le mélange n'est pas monophasique, c'est-à-dire uniquement liquide ou gazeux. Lorsque la pression est supérieure à la pression d'ébullition, soit ${\displaystyle P>P_{\text{b}}}$, le mélange est entièrement liquide. Pour une composition donnée, la fonction ${\displaystyle f\!\left(P\right)=\sum _{i=1}^{N}x_{i}K_{i}\!\left(P\right)}$ est une fonction décroissante de la pression. Lorsque ${\displaystyle f\!\left(P\right)=1}$, la pression est la pression d'ébullition ${\displaystyle P_{\text{b}}}$ aux température et composition données. Lorsque ${\displaystyle P>P_{\text{b}}}$, on a ${\displaystyle f\!\left(P\right)<1}$^[67]. Lorsque la pression est inférieure à la pression de rosée, soit ${\displaystyle P<P_{\text{r}}}$, le mélange est entièrement gazeux. Pour une composition donnée, la fonction ${\displaystyle g\!\left(P\right)=\sum _{i=1}^{N}{x_{i} \over K_{i}\!\left(P\right)}}$ est une fonction croissante de la pression. Lorsque ${\displaystyle g\!\left(P\right)=1}$, la pression est la pression de rosée ${\displaystyle P_{\text{r}}}$ aux température et composition données. Lorsque ${\displaystyle P<P_{\text{r}}}$, on a ${\displaystyle g\!\left(P\right)<1}$^[67].

On effectue par conséquent le calcul selon l'algorithme suivant.

Algorithme de calcul

1. À pression et température de l'énoncé, calculer le coefficient de partage ${\displaystyle K_{i}}$ pour chacun des ${\displaystyle N}$ constituants.
2. Si ${\displaystyle \sum _{i=1}^{N}x_{i}K_{i}<1}$ le mélange est entièrement liquide : ${\displaystyle \tau ^{\text{g}}=0}$ et pour tout constituant ${\displaystyle x_{i}^{\text{l}}=x_{i}}$ ; fin du calcul. Sinon, passer en 3.
3. Si ${\displaystyle \sum _{i=1}^{N}{x_{i} \over K_{i}}<1}$ le mélange est entièrement gazeux : ${\displaystyle \tau ^{\text{g}}=1}$ et pour tout constituant ${\displaystyle x_{i}^{\text{g}}=x_{i}}$ ; fin du calcul. Sinon, passer en 4.
4. Sinon, le mélange est biphasique et présente un équilibre liquide-vapeur. Résoudre l'équation de Rachford-Rice : ${\displaystyle \sum _{i=1}^{N}{\left(K_{i}-1\right)x_{i} \over 1+\left(K_{i}-1\right)\tau ^{\text{g}}}=0}$.

Dans le cas d'un mélange binaire, impliquant les constituants ${\displaystyle {\text{A}}}$ et ${\displaystyle {\text{B}}}$, après avoir vérifié la présence de deux phases comme précédemment, on calcule plus rapidement les compositions des phases selon^[68] :

• ${\displaystyle x_{\text{A}}^{\text{l}}={1-K_{\text{B}} \over K_{\text{A}}-K_{\text{B}}}}$ ;
• ${\displaystyle x_{\text{B}}^{\text{l}}=1-x_{\text{A}}^{\text{l}}}$ ;
• ${\displaystyle x_{\text{A}}^{\text{g}}=K_{\text{A}}x_{\text{A}}^{\text{l}}}$ ;
• ${\displaystyle x_{\text{B}}^{\text{g}}=1-x_{\text{A}}^{\text{g}}}$ ;
• ${\displaystyle \tau ^{\text{g}}={x_{\text{A}}-x_{\text{A}}^{\text{l}} \over x_{\text{A}}^{\text{g}}-x_{\text{A}}^{\text{l}}}}$.

Exemple^[66]

On considère un mélange d'hydrocarbures dans les conditions données par le tableau suivant.

Mélange d'hydrocarbures à 3,5 bar et 300 K - données.

Constituant ${\displaystyle i}$	Fraction molaire globale ${\displaystyle x_{i}}$	Coefficient de partage ${\displaystyle K_{i}}$
Propane	0,2	2,525
n-Butane	0,3	0,7708
Isobutane	0,4	1,066
n-Pentane	0,05	0,2401
Isopentane	0,05	0,3140

On a ${\displaystyle \sum _{i=1}^{N}x_{i}K_{i}}$ = 1,1903 et ${\displaystyle \sum _{i=1}^{N}{x_{i} \over K_{i}}}$ = 1,2113. Le mélange est donc biphasique. Les résultats sont reportés dans le tableau suivant.

Mélange d'hydrocarbures à 3,5 bar et 300 K - résultats.

Taux de vaporisation ${\displaystyle \tau ^{\text{g}}}$	0,524
Constituant ${\displaystyle i}$	Fraction molaire liquide ${\displaystyle x_{i}^{\text{l}}}$	Fraction molaire vapeur ${\displaystyle x_{i}^{\text{g}}}$
Propane	0,1112	0,2807
n-Butane	0,3409	0,2628
Isobutane	0,3867	0,4121
n-Pentane	0,0831	0,0199
Isopentane	0,0781	0,0245

Équilibres liquide-solide idéaux

L'équation de Schröder-van Laar permet de déterminer, à pression constante, l'équilibre liquide-solide de deux phases idéales, dans lequel seule l'espèce ${\displaystyle {\text{A}}}$ est présente dans la phase solide. Elle s'écrit en fonction de la composition de la phase liquide^[69],[70] :

Équation de Schröder-van Laar ${\displaystyle \ln x_{\text{A}}^{\text{l}}={\Delta _{\text{fus}}H_{\text{A}} \over RT_{\text{fus,A}}}\left[1-{T_{\text{fus,A}} \over T}\right]-{\Delta _{\text{fus}}C_{P,{\text{A}}} \over R}\left[1-{T_{\text{fus,A}} \over T}+\ln \!\left({T_{\text{fus,A}} \over T}\right)\right]}$

avec :

• ${\displaystyle P}$ la pression de l'équilibre liquide-solide ;
• ${\displaystyle R}$ la constante universelle des gaz parfaits ;
• ${\displaystyle T}$ la température de l'équilibre liquide-solide sous la pression ${\displaystyle P}$ ;
• ${\displaystyle T_{\text{fus,A}}}$ la température du fusion du corps ${\displaystyle {\text{A}}}$ pur sous la pression ${\displaystyle P}$ ;
• ${\displaystyle x_{\text{A}}^{\text{l}}}$ la fraction molaire du corps ${\displaystyle {\text{A}}}$ dans la phase liquide ;
• ${\displaystyle \Delta _{\text{fus}}C_{P,{\text{A}}}}$ l'écart des capacités thermiques isobares molaires du corps ${\displaystyle {\text{A}}}$ pur liquide et solide à ${\displaystyle T_{\text{fus,A}}}$ :
  • ${\displaystyle \Delta _{\text{fus}}C_{P,{\text{A}}}={\bar {C}}_{P,{\text{A}}}^{\text{l,*}}\!\left(T_{\text{fus,A}}\right)-{\bar {C}}_{P,{\text{A}}}^{\text{s,*}}\!\left(T_{\text{fus,A}}\right)}$ ;
  • ${\displaystyle {\bar {C}}_{P,{\text{A}}}^{\text{l,*}}}$ la capacité thermique isobare molaire du corps ${\displaystyle {\text{A}}}$ liquide pur ;
  • ${\displaystyle {\bar {C}}_{P,{\text{A}}}^{\text{s,*}}}$ la capacité thermique isobare molaire du corps ${\displaystyle {\text{A}}}$ solide pur ;
• ${\displaystyle \Delta _{\text{fus}}H_{\text{A}}}$ l'enthalpie de fusion du corps ${\displaystyle {\text{A}}}$ pur à ${\displaystyle T_{\text{fus,A}}}$.

Propriétés colligatives

• 
  Diagramme de phases d'un solvant pur (courbes pleines) et du même solvant en présence d'un soluté (pointillés). Les propriétés colligatives se traduisent par un déplacement des courbes d'équilibre solide-liquide et gaz-liquide.
• 
  À l'équilibre, la pression de part et d'autre de la membrane semi-perméable est plus élevée dans le compartiment de la solution que dans celui du solvant pur. La différence des pressions est appelée « pression osmotique ».

Dans une solution liquide, le « solvant » est l'espèce chimique majoritaire et le « soluté » l'espèce minoritaire. La comparaison des conditions opératoires de transition de phase du solvant pur avec celles de la solution montre que la présence du soluté modifie ces conditions : à température identique, la pression de transition est modifiée, de même qu'à pression identique la température de transition est modifiée. Dans le cas particulier où la phase en équilibre avec la solution ne contient que le solvant et où le soluté n'est présent qu'en très faible quantité dans la solution, les écarts constatés sont appelés « propriétés colligative ». Dans ces conditions, ces écarts peuvent être calculés, selon l'hypothèse de la solution idéale, à l'aide de lois ne dépendant que des propriétés du solvant et linéaires selon la concentration du soluté.

À température ${\displaystyle T}$ donnée, la pression d'équilibre liquide-vapeur de la solution est plus basse que celle du solvant pur. L'abaissement de la pression de vapeur saturante se calcule selon la loi de la tonométrie :

Loi de la tonométrie : ${\displaystyle {\Delta P^{\text{sat}} \over P^{\text{sat}}}=x_{\sigma }^{\text{l}}}$

avec :

• ${\displaystyle \Delta P^{\text{sat}}}$ l'abaissement de la pression de vapeur saturante du solvant en présence du soluté (en Pa) ; la pression d'équilibre liquide-vapeur de la solution vaut ${\displaystyle P^{\text{sat}}-\Delta P^{\text{sat}}}$ ;
• ${\displaystyle P^{\text{sat}}}$ la pression de vapeur saturante du solvant pur à la température ${\displaystyle T}$ (en Pa) ;
• ${\displaystyle x_{\sigma }^{\text{l}}}$ la fraction molaire du soluté en solution.

À pression ${\displaystyle P}$ donnée, la température d'équilibre liquide-vapeur de la solution est plus élevée que celle du solvant pur. L'élévation de la température d'ébullition se calcule selon la loi de l'ébulliométrie^[71] :

Loi de l'ébulliométrie : ${\displaystyle \Delta T_{\text{vap}}=K_{\text{éb}}\cdot x_{\sigma }^{\text{l}}}$ Constante ébullioscopique : ${\displaystyle K_{\text{éb}}={R\,{T_{\text{vap}}}^{2} \over \Delta _{\text{vap}}H}}$

avec :

• ${\displaystyle \Delta T_{\text{vap}}}$ l'élévation de la température d'ébullition du solvant (en K) ; la température d'ébullition de la solution vaut ${\displaystyle T_{\text{vap}}+\Delta T_{\text{vap}}}$ ;
• ${\displaystyle T_{\text{vap}}}$ la température d'ébullition du solvant pur à la pression ${\displaystyle P}$ (en K) ;
• ${\displaystyle \Delta _{\text{vap}}H}$ l'enthalpie de vaporisation du solvant pur à ${\displaystyle T_{\text{vap}}}$ (en J mol⁻¹) ;
• ${\displaystyle R}$ la constante universelle des gaz parfaits (en J K⁻¹ mol⁻¹).

À pression ${\displaystyle P}$ donnée, la température d'équilibre liquide-solide de la solution est plus basse que celle du solvant pur. L'abaissement de la température de fusion (ou température de solidification ou température de congélation) se calcule selon la loi de la cryométrie^[72] :

Loi de la cryométrie : ${\displaystyle \Delta T_{\text{fus}}=K_{\text{cry}}\cdot x_{\sigma }^{\text{l}}}$ Constante cryoscopique : ${\displaystyle K_{\text{cry}}={R\,{T_{\text{fus}}}^{2} \over \Delta _{\text{fus}}H}}$

avec :

• ${\displaystyle \Delta T_{\text{fus}}}$ l'abaissement de la température de fusion du solvant (en K) ; la température de fusion de la solution vaut ${\displaystyle T_{\text{fus}}-\Delta T_{\text{fus}}}$ ;
• ${\displaystyle T_{\text{fus}}}$ la température de fusion du solvant pur à la pression ${\displaystyle P}$ (en K) ;
• ${\displaystyle \Delta _{\text{fus}}H}$ l'enthalpie de fusion du solvant pur à ${\displaystyle T_{\text{fus}}}$ (en J mol⁻¹).

À température ${\displaystyle T}$ donnée, si l'on place la solution et le solvant pur de part et d'autre d'une membrane semi-perméable (ne laissant passer que le solvant), la pression d'équilibre est plus élevée dans le compartiment de la solution que dans celui du solvant. La différence de pression entre les deux compartiments, appelée « pression osmotique », se calcule selon la loi de l'osmométrie^[73] :

Loi de van 't Hoff, ou loi de l'osmométrie : ${\displaystyle \Pi =c_{\sigma }^{\text{l}}RT}$

avec :

• ${\displaystyle \Pi }$ la pression osmotique (en Pa) ; si au niveau de la membrane la pression du compartiment du solvant pur vaut ${\displaystyle P}$, celle du côté de la solution vaut ${\displaystyle P+\Pi }$ ;
• ${\displaystyle c_{\sigma }^{\text{l}}}$ la concentration molaire du soluté en solution (en mol m⁻³) ;
• ${\displaystyle T}$ la température (en K).

Notations

Alphabet latin

Alphabet grec

Notes et références

Notes

Bibliographie

• Christophe Coquelet et Dominique Richon, Propriétés thermodynamiques : Détermination pour les mélanges, vol. BE 8 031, Techniques de l'ingénieur, 2007, 12 p. (lire en ligne).
• Jean-Pierre Corriou, Thermodynamique chimique : Diagrammes thermodynamiques, vol. J 1 026, Techniques de l'ingénieur, 1985a (lire en ligne).
• Jean-Pierre Corriou, Thermodynamique chimique : Équilibres thermodynamiques, vol. J 1 028, Techniques de l'ingénieur, 1985b (lire en ligne).
• Walter Greiner, Ludwig Neise et Horst Stöcker (trad. de l'anglais par Hans Aksas), Thermodynamique et mécanique statistique [« Thermodynamics and Statistical Mechanics »], New York, Springer, 1999, 532 p. (ISBN 9783540661665, lire en ligne).
• P. Infelta et M. Graetzel, Thermodynamique : Principes et Applications, BrownWalker Press, 2006, 484 p. (ISBN 978-1-58112-995-3, lire en ligne).
• (en) M. Scott Shell, Thermodynamics and Statistical Mechanics : An Integrated Approach, Cambridge University Press, 2015, 476 p. (ISBN 9781107014534, lire en ligne), p. 220-221, 250-253.
• Michel Soustelle, Transformations entre phases, vol. 5, ISTE Group, coll. « Génie des procédés / Thermodynamique chimique approfondie », 2016, 240 p. (ISBN 9781784051235, lire en ligne).
• Richard Taillet, Loïc Villain et Pascal Febvre, Dictionnaire de physique : + de 6500 termes, nombreuses références historiques, des milliers de références bibliographiques, Louvain-la-Neuve/impr. aux Pays-Bas, De Boeck supérieur, 2018, 976 p. (ISBN 978-2-8073-0744-5, lire en ligne).
• Jean Vidal, Thermodynamique : Application au génie chimique et à l'industrie pétrolière, Paris, Éditions Technip, coll. « Publications de l'Institut français du pétrole. », 1997, 500 p. (ISBN 978-2-7108-0715-5, OCLC 300489419, lire en ligne).

Articles connexes

• Portail de la physique