Illustration de la sensibilité aux conditions initiales avec trois pendules doubles aux conditions de départ très proches. En mécanique , on désigne par pendule double un pendule à l'extrémité duquel on accroche un autre pendule. Son évolution est généralement chaotique .
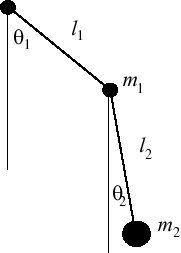
Mise en équations Un pendule double est un système dynamique typiquement limité à un mouvement plan . Il comporte deux degrés de libertés ( θ 1 , θ 2 {\displaystyle \theta _{1},\,\theta _{2}} l 1 , l 2 , m 1 , m 2 , g {\displaystyle l_{1},\,l_{2},\,m_{1},\,m_{2},\,g}
Le pendule est constitué de deux tiges de longueur l 1 {\displaystyle l_{1}\,} l 2 {\displaystyle l_{2}\,} m 1 {\displaystyle m_{1}\,} m 2 {\displaystyle m_{2}\,}
L'énergie cinétique vaut : T = 1 2 m 1 v 1 2 + 1 2 m 2 v 2 2 = 1 2 m 1 l 1 2 θ ˙ 1 2 + 1 2 m 2 [ l 1 2 θ ˙ 1 2 + l 2 2 θ ˙ 2 2 + 2 l 1 l 2 θ ˙ 1 θ ˙ 2 cos ( θ 1 − θ 2 ) ] {\displaystyle T={\frac {1}{2}}m_{1}v_{1}^{2}+{\frac {1}{2}}m_{2}v_{2}^{2}={\frac {1}{2}}m_{1}l_{1}^{2}{\dot {\theta }}_{1}^{2}+{\frac {1}{2}}m_{2}[l_{1}^{2}{\dot {\theta }}_{1}^{2}+l_{2}^{2}{\dot {\theta }}_{2}^{2}+2l_{1}l_{2}{\dot {\theta }}_{1}{\dot {\theta }}_{2}\cos(\theta _{1}-\theta _{2})]} θ i {\displaystyle \theta _{i}\,} v i {\displaystyle v_{i}\,} i {\displaystyle i\,} V = m 1 g z 1 + m 2 g z 2 {\displaystyle V=m_{1}gz_{1}+m_{2}gz_{2}\,} z i {\displaystyle z_{i}\,} i {\displaystyle i\,} V = − ( m 1 + m 2 ) g l 1 cos ( θ 1 ) − m 2 g l 2 cos ( θ 2 ) {\displaystyle V=-(m_{1}+m_{2})gl_{1}\cos(\theta _{1})-m_{2}gl_{2}\cos(\theta _{2})\,} L = T − V {\displaystyle L=T-V\,} L = 1 2 ( m 1 + m 2 ) l 1 2 θ ˙ 1 2 + 1 2 m 2 l 2 2 θ ˙ 2 2 + m 2 l 1 l 2 θ ˙ 1 θ ˙ 2 cos ( θ 1 − θ 2 ) + ( m 1 + m 2 ) g l 1 cos ( θ 1 ) + m 2 g l 2 cos ( θ 2 ) {\displaystyle L={\frac {1}{2}}(m_{1}+m_{2})l_{1}^{2}{\dot {\theta }}_{1}^{2}+{\frac {1}{2}}m_{2}l_{2}^{2}{\dot {\theta }}_{2}^{2}+m_{2}l_{1}l_{2}{\dot {\theta }}_{1}{\dot {\theta }}_{2}\cos(\theta _{1}-\theta _{2})+(m_{1}+m_{2})gl_{1}\cos(\theta _{1})+m_{2}gl_{2}\cos(\theta _{2})}
En appliquant les équations de Lagrange , on obtient les équations du mouvement :
( m 1 + m 2 ) l 1 θ ¨ 1 + m 2 l 2 θ ¨ 2 cos ( θ 1 − θ 2 ) + m 2 l 2 θ ˙ 2 2 sin ( θ 1 − θ 2 ) + ( m 1 + m 2 ) g sin ( θ 1 ) = 0 l 1 θ ¨ 1 cos ( θ 1 − θ 2 ) + l 2 θ ¨ 2 − l 1 θ ˙ 1 2 sin ( θ 1 − θ 2 ) + g sin ( θ 2 ) = 0 {\displaystyle {\begin{array}{l}(m_{1}+m_{2})l_{1}{\ddot {\theta }}_{1}+m_{2}l_{2}{\ddot {\theta }}_{2}\cos(\theta _{1}-\theta _{2})+m_{2}l_{2}{\dot {\theta }}_{2}^{2}\sin(\theta _{1}-\theta _{2})+(m_{1}+m_{2})g\sin(\theta _{1})=0\\l_{1}{\ddot {\theta }}_{1}\cos(\theta _{1}-\theta _{2})+l_{2}{\ddot {\theta }}_{2}-l_{1}{\dot {\theta }}_{1}^{2}\sin(\theta _{1}-\theta _{2})+g\sin(\theta _{2})=0\end{array}}}
Dans le cas particulier m 1 = m 2 , l 1 = l 2 {\displaystyle m_{1}=m_{2},\,l_{1}=l_{2}} système d'unités idoine, en renommant θ 1 , θ 2 {\displaystyle \theta _{1},\theta _{2}} ϕ , ψ {\displaystyle \phi ,\psi } δ = ϕ − ψ {\displaystyle \delta =\phi -\psi }
2 ϕ ¨ + ψ ¨ cos ( δ ) + ψ ˙ 2 sin ( δ ) + 2 sin ( ϕ ) = 0 ψ ¨ + ϕ ¨ cos ( δ ) + sin ( ψ ) = ϕ ˙ 2 sin ( δ ) δ = ϕ − ψ {\displaystyle {\begin{array}{l}2{\ddot {\phi }}+{\ddot {\psi }}\cos \left(\delta \right)+{\dot {\psi }}^{2}\sin \left(\delta \right)+2\sin \left(\phi \right)=0\\{\ddot {\psi }}+{\ddot {\phi }}\cos \left(\delta \right)+\sin \left(\psi \right)={\dot {\phi }}^{2}\sin \left(\delta \right)\\\delta =\phi -\psi \\\end{array}}} Aucune solution explicite n'étant connue, la résolution passe typiquement par l'utilisation de méthodes numériques .
Autour du minimum énergétique (voir section suivante), ce système possède des solutions périodiques décomposables en deux modes, mais il est chaotique , c’est-à-dire qu'il possède aussi des solutions ni périodiques ni pseudo-périodiques , mais présentant en permanence un mouvement original, et qu'il est alors sensible aux conditions initiales .
Approximation des petites oscillations Le système est à l'équilibre pour θ 1 = θ 2 = θ ˙ 1 = θ ˙ 2 = 0 {\displaystyle \theta _{1}=\theta _{2}={\dot {\theta }}_{1}={\dot {\theta }}_{2}=0} approximations de MacLaurin sin θ = θ {\displaystyle \sin \theta =\theta } cos θ = 1 {\displaystyle \cos \theta =1} système linéaire :
( m 1 + m 2 ) l 1 θ ¨ 1 + m 2 l 2 θ ¨ 2 + ( m 1 + m 2 ) g θ 1 = 0 l 1 θ ¨ 1 + l 2 θ ¨ 2 + g θ 2 = 0 {\displaystyle {\begin{alignedat}{5}(m_{1}+m_{2})l_{1}{\ddot {\theta }}_{1}&&\;+\;&&m_{2}l_{2}{\ddot {\theta }}_{2}&&\;+\;&&(m_{1}+m_{2})g\theta _{1}&&\;=\;&&0&\\l_{1}{\ddot {\theta }}_{1}&&\;+\;&&l_{2}{\ddot {\theta }}_{2}&&\;+\;&&g\theta _{2}&&\;=\;&&0&\end{alignedat}}} Le double pendule peut alors être analysé en termes de modes normaux, en remarquant que le système ci-dessus peut être réduit à la forme matricielle M θ → ¨ + K θ → = 0 → {\displaystyle M{\ddot {\vec {\theta }}}+K{\vec {\theta }}={\vec {0}}}
Par exemple, pour m 1 = m 2 {\displaystyle m_{1}=m_{2}} l 1 = l 2 = l {\displaystyle l_{1}=l_{2}=l} [ θ ¨ 1 θ ¨ 2 ] = g l [ − 2 1 2 − 2 ] [ θ 1 θ 2 ] {\displaystyle {\begin{bmatrix}{\ddot {\theta }}_{1}\\{\ddot {\theta }}_{2}\end{bmatrix}}={\frac {g}{l}}{\begin{bmatrix}-2&1\\2&-2\end{bmatrix}}{\begin{bmatrix}\theta _{1}\\\theta _{2}\end{bmatrix}}}
Approche Newtonienne Les équations du mouvement peuvent également être trouvées en utilisant les complexes.
Représentons le double pendule ci-dessus dans le plan complexe de Gauss, en posant que l’axe des réels a même sens et même direction que la gravitation. Les points m1 et m2 représentant les mobiles 1 et 2 correspondent aux affixes z1 et z2 . En fait, seuls les angles vont varier en fonction du temps puisque la masse et la longueur sont des constantes. Il faut donc chercher une manière de représenter les fonctions θ 1 {\displaystyle \theta _{1}} θ 2 {\displaystyle \theta _{2}}
Dès lors, puisque le module de z1 vaut l1 , son argument θ 1 {\displaystyle \theta _{1}} z 1 = l 1 ( cos θ 1 + i sin θ 1 ) = l 1 e i θ 1 {\displaystyle z_{1}=l_{1}(\cos \theta _{1}+i\sin \theta _{1})=l_{1}e^{i\theta _{1}}} 2 est issu d’une translation de z1 par le complexe z0 = l 2 e i θ 2 {\displaystyle l_{2}e^{i\theta _{2}}} 2 et son argument θ 2 {\displaystyle \theta _{2}} 2 = z1 + z0 , donc z 2 = l 1 e i θ 1 + l 2 e i θ 2 {\displaystyle z_{2}=l_{1}e^{i\theta _{1}}+l_{2}e^{i\theta _{2}}}
Ici, les complexes z1 et z2 déterminent la position des mobiles1 et 2 en fonction du temps puisque θ 1 ( t ) {\displaystyle \theta _{1}(t)} θ 2 ( t ) {\displaystyle \theta _{2}(t)} 1 vaut
a z 1 = d 2 z 1 d t 2 = l 1 ( i θ ¨ 1 − θ ˙ 1 2 ) e i θ 1 {\displaystyle a_{z_{1}}={\operatorname {d^{2}} \!z_{1} \over \operatorname {d} \!t^{2}}=l_{1}(i{\ddot {\theta }}_{1}-{\dot {\theta }}_{1}^{2})e^{i\theta _{1}}}
et que celle de la deuxième est égale à
a z 2 = d 2 z 2 d t 2 = l 1 ( i θ ¨ 1 − θ ˙ 1 2 ) e i θ 1 + l 2 ( i θ ¨ 2 − θ ˙ 2 2 ) e i θ 2 {\displaystyle a_{z_{2}}={\operatorname {d^{2}} \!z_{2} \over \operatorname {d} \!t^{2}}=l_{1}(i{\ddot {\theta }}_{1}-{\dot {\theta }}_{1}^{2})e^{i\theta _{1}}+l_{2}(i{\ddot {\theta }}_{2}-{\dot {\theta }}_{2}^{2})e^{i\theta _{2}}}
Notons-les respectivement z ¨ 1 {\displaystyle {\ddot {z}}_{1}} z ¨ 2 {\displaystyle {\ddot {z}}_{2}}
Revenons dans la vie réelle. Quand une masse est suspendue à une corde, une tension se produit le long de celle-ci. Appelons, T1 et T2 , les tensions exercées par les masses m1 et m2 et représentons-les sous forme de complexes t1 et t2 .
Nous observons alors que t1 , z1 et 0 sont alignés ou colinéaires, ce qui permet d’écrire que t 1 = k 1 z 1 ( k 1 ∈ R ) {\displaystyle t_{1}=k_{1}z_{1}\,(k_{1}\in \mathbb {R} )} 2 , z0 et 0 sont alignés, ce qui permet d’affirmer que t 2 = k 2 z 0 ( k 2 ∈ R ) {\displaystyle t_{2}=k_{2}z_{0}\,(k_{2}\in \mathbb {R} )}
La formule de la dynamique F = m a , connue aussi sous le nom de la 2e loi de Newton, dit que la somme de toutes les forces appliquées à un mobile est égale au produit de l’accélération de celui-ci par sa masse.
Le mobile 2 est soumis à la tension T2 et la force due à la gravité m2 g, donnant les relations suivantes :
F = m a z 2 = t 2 + m 2 g ⟺ m 2 z ¨ 2 − m 2 g = t 2 ⟺ z ¨ 2 − g = t 2 m 2 = k 2 z 0 m 2 ⇒ z ¨ 2 − g z 0 = k 2 m 2 . . . ( 1 ) {\displaystyle F=ma_{z_{2}}=t_{2}+m_{2}g\Longleftrightarrow m_{2}{\ddot {z}}_{2}-m_{2}g=t_{2}\Longleftrightarrow {\ddot {z}}_{2}-g={\frac {t_{2}}{m_{2}}}={\frac {k_{2}z_{0}}{m_{2}}}\,\Rightarrow \,{\frac {{\ddot {z}}_{2}-g}{z_{0}}}={\frac {k_{2}}{m_{2}}}\,...(1)}
Le mobile 1 est soumis à la tension T1 , à la force due à la gravité m1 g et à la tension T2 ’ qui est issue du principe des actions réciproques (la 3e loi de Newton) telle que T2 ’= - T2 . Dès lors, nous pouvons dire que
F = m a z 1 = t 1 − t 2 + m 1 g ⟺ t 1 = t 2 − m 1 g + m 1 z ¨ 1 ⟺ t 1 = m 2 z ¨ 2 − m 2 g − m 1 g + m 1 z ¨ 1 {\displaystyle F=ma_{z_{1}}=t_{1}-t_{2}+m_{1}g\Longleftrightarrow t_{1}=t_{2}-m_{1}g+m_{1}{\ddot {z}}_{1}\Longleftrightarrow t_{1}=m_{2}{\ddot {z}}_{2}-m_{2}g-m_{1}g+m_{1}{\ddot {z}}_{1}}
⟺ m 2 z ¨ 2 − m 2 g − m 1 g + m 1 z ¨ 1 = k 1 z 1 ⟺ m 2 z ¨ 2 − m 2 g − m 1 g + m 1 z ¨ 1 z 1 = k 1 . . . ( 2 ) {\displaystyle \Longleftrightarrow m_{2}{\ddot {z}}_{2}-m_{2}g-m_{1}g+m_{1}{\ddot {z}}_{1}=k_{1}z_{1}\Longleftrightarrow {\frac {m_{2}{\ddot {z}}_{2}-m_{2}g-m_{1}g+m_{1}{\ddot {z}}_{1}}{z_{1}}}=k_{1}\,...(2)}
Les membres de droite des équations (1) et (2) étant réels, exprimons que la partie imaginaire des membres de gauche est nulle :
Tout d’abord, concernant l’équation (1).
Calculons le membre de gauche.
z ¨ 2 − g z 0 = l 1 ( i θ ¨ 1 − θ ˙ 1 2 ) e i θ 1 + l 2 ( i θ ¨ 2 − θ ˙ 2 2 ) e i θ 2 − g l 2 e i θ 2 {\displaystyle {\frac {{\ddot {z}}_{2}-g}{z_{0}}}={\frac {l_{1}(i{\ddot {\theta }}_{1}-{\dot {\theta }}_{1}^{2})e^{i\theta _{1}}+l_{2}(i{\ddot {\theta }}_{2}-{\dot {\theta }}_{2}^{2})e^{i\theta _{2}}-g}{l_{2}e^{i\theta _{2}}}}}
= l 1 i θ ¨ 1 cos θ 1 − l 1 θ ˙ 1 2 cos θ 1 − l 1 θ ¨ 1 sin θ 1 − l 1 i θ ˙ 1 2 sin θ 1 + l 2 i θ ¨ 2 cos θ 2 − l 2 θ ˙ 2 2 cos θ 2 − l 2 θ ¨ 2 sin θ 2 − l 2 i θ ˙ 2 2 sin θ 2 − g l 2 cos θ 2 + l 2 i sin θ 2 {\displaystyle ={\frac {l_{1}i{\ddot {\theta }}_{1}\cos \theta _{1}-l_{1}{\dot {\theta }}_{1}^{2}\cos \theta _{1}-l_{1}{\ddot {\theta }}_{1}\sin \theta _{1}-l_{1}i{\dot {\theta }}_{1}^{2}\sin \theta _{1}+l_{2}i{\ddot {\theta }}_{2}\cos \theta _{2}-l_{2}{\dot {\theta }}_{2}^{2}\cos \theta _{2}-l_{2}{\ddot {\theta }}_{2}\sin \theta _{2}-l_{2}i{\dot {\theta }}_{2}^{2}\sin \theta _{2}-g}{l_{2}\cos \theta _{2}+l_{2}i\sin \theta _{2}}}}
Appliquons le binôme conjugué pour supprimer le terme imaginaire au dénominateur, ce qui revient à multiplier la fraction par cos θ 2 − i sin θ 2 cos θ 2 − i sin θ 2 {\displaystyle {\frac {\cos \theta _{2}-i\sin \theta _{2}}{\cos \theta _{2}-i\sin \theta _{2}}}}
Maintenant, seuls les imaginaires purs intéressent. C’est pourquoi, relevons uniquement les imaginaires purs issus du produit du numérateur par le conjugué du dénominateur. Nous conservons alors uniquement :
( l 1 i θ ¨ 1 cos θ 1 − l 1 i θ ˙ 1 2 sin θ 1 + l 2 i θ ¨ 2 cos θ 2 − l 2 i θ ˙ 2 2 sin θ 2 ) ( cos θ 2 ) {\displaystyle (l_{1}i{\ddot {\theta }}_{1}\cos \theta _{1}-l_{1}i{\dot {\theta }}_{1}^{2}\sin \theta _{1}+l_{2}i{\ddot {\theta }}_{2}\cos \theta _{2}-l_{2}i{\dot {\theta }}_{2}^{2}\sin \theta _{2})(\cos \theta _{2})}
+ ( − l 1 θ ˙ 1 2 cos θ 1 − l 1 θ ¨ 1 sin θ 1 − l 2 θ ˙ 2 2 cos θ 2 − l 2 θ ¨ 2 sin θ 2 − g ) ( − i sin θ 2 ) {\displaystyle +(-l_{1}{\dot {\theta }}_{1}^{2}\cos \theta _{1}-l_{1}{\ddot {\theta }}_{1}\sin \theta _{1}-l_{2}{\dot {\theta }}_{2}^{2}\cos \theta _{2}-l_{2}{\ddot {\theta }}_{2}\sin \theta _{2}-g)(-i\sin \theta _{2})}
Ainsi, nous pouvons affirmer que :
Im ( z ¨ 2 − g z 0 ) {\displaystyle {\text{Im}}({\frac {{\ddot {z}}_{2}-g}{z_{0}}})}
= l 1 θ ¨ 1 cos θ 1 cos θ 2 − l 1 θ ˙ 1 2 sin θ 1 cos θ 2 + l 2 θ ¨ 2 cos 2 θ 2 − l 2 θ ˙ 2 2 cos θ 2 sin θ 2 l 2 {\displaystyle ={\frac {l_{1}{\ddot {\theta }}_{1}\cos \theta _{1}\cos \theta _{2}-l_{1}{\dot {\theta }}_{1}^{2}\sin \theta _{1}\cos \theta _{2}+l_{2}{\ddot {\theta }}_{2}\cos ^{2}\theta _{2}-l_{2}{\dot {\theta }}_{2}^{2}\cos \theta _{2}\sin \theta _{2}}{l_{2}}}}
+ l 1 θ ˙ 1 2 sin θ 2 cos θ 1 + l 1 θ ¨ 1 sin θ 1 sin θ 2 + l 2 θ ˙ 2 2 sin θ 2 cos θ 2 + l 2 θ ¨ 2 sin 2 θ 2 + g sin θ 2 l 2 {\displaystyle +{\frac {l_{1}{\dot {\theta }}_{1}^{2}\sin \theta _{2}\cos \theta _{1}+l_{1}{\ddot {\theta }}_{1}\sin \theta _{1}\sin \theta _{2}+l_{2}{\dot {\theta }}_{2}^{2}\sin \theta _{2}\cos \theta _{2}+l_{2}{\ddot {\theta }}_{2}\sin ^{2}\theta _{2}+g\sin \theta _{2}}{l_{2}}}}
= l 1 θ ¨ 1 cos ( θ 1 − θ 2 ) + l 2 θ ¨ 2 − l 1 θ ˙ 1 2 sin ( θ 1 − θ 2 ) + g sin ( θ 2 ) l 2 {\displaystyle ={\frac {l_{1}{\ddot {\theta }}_{1}\cos(\theta _{1}-\theta _{2})+l_{2}{\ddot {\theta }}_{2}-l_{1}{\dot {\theta }}_{1}^{2}\sin(\theta _{1}-\theta _{2})+g\sin(\theta _{2})}{l_{2}}}}
Comme il faut que la partie imaginaire soit nulle, nous obtenons cette première équation différentielle.
l 1 θ ¨ 1 cos ( θ 1 − θ 2 ) + l 2 θ ¨ 2 − l 1 θ ˙ 1 2 sin ( θ 1 − θ 2 ) + g sin ( θ 2 ) = 0 {\displaystyle l_{1}{\ddot {\theta }}_{1}\cos(\theta _{1}-\theta _{2})+l_{2}{\ddot {\theta }}_{2}-l_{1}{\dot {\theta }}_{1}^{2}\sin(\theta _{1}-\theta _{2})+g\sin(\theta _{2})=0}
Ensuite, concernant l’équation (2). Nous procédons de la même manière. Calculons le membre de gauche.
m 2 z ¨ 2 − m 2 g − m 1 g + m 1 z ¨ 1 z 1 {\displaystyle {\frac {m_{2}{\ddot {z}}_{2}-m_{2}g-m_{1}g+m_{1}{\ddot {z}}_{1}}{z_{1}}}}
= m 2 [ l 1 ( i θ ¨ 1 − θ ˙ 1 2 ) ( cos θ 1 + i sin θ 1 ) + l 2 ( i θ ¨ 2 − θ ˙ 2 2 ) ( cos θ 2 + i sin θ 2 ) ] − m 2 g − m 1 g + m 1 [ l 1 ( i θ ¨ 1 − θ ˙ 1 2 ) ( cos θ 1 + i sin θ 1 ) ] l 1 cos θ 1 + l 1 i sin θ 1 {\displaystyle ={\frac {m_{2}[l_{1}(i{\ddot {\theta }}_{1}-{\dot {\theta }}_{1}^{2})(\cos \theta _{1}+i\sin \theta _{1})+l_{2}(i{\ddot {\theta }}_{2}-{\dot {\theta }}_{2}^{2})(\cos \theta _{2}+i\sin \theta _{2})]-m_{2}g-m_{1}g+m_{1}[l_{1}(i{\ddot {\theta }}_{1}-{\dot {\theta }}_{1}^{2})(\cos \theta _{1}+i\sin \theta _{1})]}{l_{1}\cos \theta _{1}+l_{1}i\sin \theta _{1}}}}
= m 1 [ l 1 i θ ¨ 1 cos θ 1 − l 1 θ ˙ 1 2 cos θ 1 − l 1 θ ¨ 1 sin θ 1 − l 1 i θ ˙ 1 2 sin θ 1 ] − m 1 g − m 2 g l 1 cos θ 1 + l 1 i sin θ 1 {\displaystyle ={\frac {m_{1}[l_{1}i{\ddot {\theta }}_{1}\cos \theta _{1}-l_{1}{\dot {\theta }}_{1}^{2}\cos \theta _{1}-l_{1}{\ddot {\theta }}_{1}\sin \theta _{1}-l_{1}i{\dot {\theta }}_{1}^{2}\sin \theta _{1}]-m_{1}g-m_{2}g}{l_{1}\cos \theta _{1}+l_{1}i\sin \theta _{1}}}}
+ m 2 [ l 1 i θ ¨ 1 cos θ 1 − l 1 θ ˙ 1 2 cos θ 1 − l 1 θ ¨ 1 sin θ 1 − l 1 i θ ˙ 1 2 sin θ 1 + l 2 i θ ¨ 2 cos θ 2 − l 2 θ ˙ 2 2 cos θ 2 − l 2 θ ¨ 2 sin θ 2 − l 2 i θ ˙ 2 2 sin θ 2 ] l 1 cos θ 1 + l 1 i sin θ 1 {\displaystyle +{\frac {m_{2}[l_{1}i{\ddot {\theta }}_{1}\cos \theta _{1}-l_{1}{\dot {\theta }}_{1}^{2}\cos \theta _{1}-l_{1}{\ddot {\theta }}_{1}\sin \theta _{1}-l_{1}i{\dot {\theta }}_{1}^{2}\sin \theta _{1}+l_{2}i{\ddot {\theta }}_{2}\cos \theta _{2}-l_{2}{\dot {\theta }}_{2}^{2}\cos \theta _{2}-l_{2}{\ddot {\theta }}_{2}\sin \theta _{2}-l_{2}i{\dot {\theta }}_{2}^{2}\sin \theta _{2}]}{l_{1}\cos \theta _{1}+l_{1}i\sin \theta _{1}}}}
Appliquons le binôme conjugué pour supprimer le terme imaginaire au dénominateur, ce qui revient à multiplier la fraction par cos θ 1 − i sin θ 1 cos θ 1 − i sin θ 1 {\displaystyle {\frac {\cos \theta _{1}-i\sin \theta _{1}}{\cos \theta _{1}-i\sin \theta _{1}}}}
Maintenant, seuls les imaginaires purs intéressent. C’est pourquoi, relevons uniquement les imaginaires purs issus du produit du numérateur par le conjugué du dénominateur. Nous gardons alors uniquement
[ m 1 ( l 1 i θ ¨ 1 cos θ 1 − l 1 i θ ˙ 1 2 sin θ 1 ) + m 2 ( l 1 i θ ¨ 1 cos θ 1 − l 1 i θ ˙ 1 2 sin θ 1 + l 2 i θ ¨ 2 cos θ 2 − l 2 i θ ˙ 2 2 sin θ 2 ) ] [ cos θ 1 ] {\displaystyle [m_{1}(l_{1}i{\ddot {\theta }}_{1}\cos \theta _{1}-l_{1}i{\dot {\theta }}_{1}^{2}\sin \theta _{1})+m_{2}(l_{1}i{\ddot {\theta }}_{1}\cos \theta _{1}-l_{1}i{\dot {\theta }}_{1}^{2}\sin \theta _{1}+l_{2}i{\ddot {\theta }}_{2}\cos \theta _{2}-l_{2}i{\dot {\theta }}_{2}^{2}\sin \theta _{2})][\cos \theta _{1}]}
+ [ m 1 ( − l 1 θ ˙ 1 2 cos θ 1 − l 1 θ ¨ 1 sin θ 1 ) + m 2 ( − l 1 θ ˙ 1 2 cos θ 1 − l 1 θ ¨ 1 sin θ 1 − l 2 θ ˙ 2 2 cos θ 2 − l 2 θ ¨ 2 sin θ 2 ) − m 1 g − m 2 g ] [ − i sin θ 1 ] {\displaystyle +[m_{1}(-l_{1}{\dot {\theta }}_{1}^{2}\cos \theta _{1}-l_{1}{\ddot {\theta }}_{1}\sin \theta _{1})+m_{2}(-l_{1}{\dot {\theta }}_{1}^{2}\cos \theta _{1}-l_{1}{\ddot {\theta }}_{1}\sin \theta _{1}-l_{2}{\dot {\theta }}_{2}^{2}\cos \theta _{2}-l_{2}{\ddot {\theta }}_{2}\sin \theta _{2})-m_{1}g-m_{2}g][-i\sin \theta _{1}]}
Ainsi, nous pouvons affirmer que
Im ( m 2 z ¨ 2 − m 2 g − m 1 g + m 1 z ¨ 1 z 1 ) {\displaystyle {\text{Im}}({\frac {m_{2}{\ddot {z}}_{2}-m_{2}g-m_{1}g+m_{1}{\ddot {z}}_{1}}{z_{1}}})}
= m 1 l 1 θ ¨ 1 cos 2 θ 1 − m 1 l 1 θ ˙ 1 2 sin θ 1 cos θ 1 + m 2 l 1 θ ¨ 1 cos 2 θ 1 − m 2 l 1 θ ˙ 1 2 sin θ 1 cos θ 1 + m 2 l 2 θ ¨ 2 cos θ 1 cos θ 2 l 1 {\displaystyle ={\frac {m_{1}l_{1}{\ddot {\theta }}_{1}\cos ^{2}\theta _{1}-m_{1}l_{1}{\dot {\theta }}_{1}^{2}\sin \theta _{1}\cos \theta _{1}+m_{2}l_{1}{\ddot {\theta }}_{1}\cos ^{2}\theta _{1}-m_{2}l_{1}{\dot {\theta }}_{1}^{2}\sin \theta _{1}\cos \theta _{1}+m_{2}l_{2}{\ddot {\theta }}_{2}\cos \theta _{1}\cos \theta _{2}}{l_{1}}}}
+ − m 2 l 2 θ ˙ 2 2 sin θ 2 cos θ 1 + m 1 l 1 θ ˙ 1 2 sin θ 1 cos θ 1 + m 1 l 1 θ ¨ 1 sin 2 θ 1 + m 2 l 1 θ ˙ 1 2 sin θ 1 cos θ 1 + m 2 l 1 θ ¨ 1 sin 2 θ 1 l 1 {\displaystyle +{\frac {-m_{2}l_{2}{\dot {\theta }}_{2}^{2}\sin \theta _{2}\cos \theta _{1}+m_{1}l_{1}{\dot {\theta }}_{1}^{2}\sin \theta _{1}\cos \theta _{1}+m_{1}l_{1}{\ddot {\theta }}_{1}\sin ^{2}\theta _{1}+m_{2}l_{1}{\dot {\theta }}_{1}^{2}\sin \theta _{1}\cos \theta _{1}+m_{2}l_{1}{\ddot {\theta }}_{1}\sin ^{2}\theta _{1}}{l_{1}}}}
+ m 2 l 2 θ ˙ 2 2 sin θ 1 cos θ 2 + m 2 l 2 θ ¨ 2 sin θ 1 sin θ 2 + m 1 sin θ 1 g + m 2 sin θ 1 g l 1 {\displaystyle +{\frac {m_{2}l_{2}{\dot {\theta }}_{2}^{2}\sin \theta _{1}\cos \theta _{2}+m_{2}l_{2}{\ddot {\theta }}_{2}\sin \theta _{1}\sin \theta _{2}+m_{1}\sin \theta _{1}g+m_{2}\sin \theta _{1}g}{l_{1}}}}
= ( m 1 + m 2 ) l 1 θ ¨ 1 + m 2 l 2 θ ¨ 2 cos ( θ 1 − θ 2 ) + m 2 l 2 θ ˙ 2 2 sin ( θ 1 − θ 2 ) + ( m 1 + m 2 ) g sin ( θ 1 ) l 1 {\displaystyle ={\frac {(m_{1}+m_{2})l_{1}{\ddot {\theta }}_{1}+m_{2}l_{2}{\ddot {\theta }}_{2}\cos(\theta _{1}-\theta _{2})+m_{2}l_{2}{\dot {\theta }}_{2}^{2}\sin(\theta _{1}-\theta _{2})+(m_{1}+m_{2})g\sin(\theta _{1})}{l_{1}}}}
Comme il faut que la partie imaginaire soit nulle, nous obtenons cette deuxième différentielle.
( m 1 + m 2 ) l 1 θ ¨ 1 + m 2 l 2 θ ¨ 2 cos ( θ 1 − θ 2 ) + m 2 l 2 θ ˙ 2 2 sin ( θ 1 − θ 2 ) + ( m 1 + m 2 ) g sin ( θ 1 ) = 0 {\displaystyle (m_{1}+m_{2})l_{1}{\ddot {\theta }}_{1}+m_{2}l_{2}{\ddot {\theta }}_{2}\cos(\theta _{1}-\theta _{2})+m_{2}l_{2}{\dot {\theta }}_{2}^{2}\sin(\theta _{1}-\theta _{2})+(m_{1}+m_{2})g\sin(\theta _{1})=0}
Nous avons donc pour finir :
{ l 1 θ ¨ 1 cos ( θ 1 − θ 2 ) + l 2 θ ¨ 2 − l 1 θ ˙ 1 2 sin ( θ 1 − θ 2 ) + g sin ( θ 2 ) = 0 ( m 1 + m 2 ) l 1 θ ¨ 1 + m 2 l 2 θ ¨ 2 cos ( θ 1 − θ 2 ) + m 2 l 2 θ ˙ 2 2 sin ( θ 1 − θ 2 ) + ( m 1 + m 2 ) g sin ( θ 1 ) = 0 {\displaystyle {\begin{cases}l_{1}{\ddot {\theta }}_{1}\cos(\theta _{1}-\theta _{2})+l_{2}{\ddot {\theta }}_{2}-l_{1}{\dot {\theta }}_{1}^{2}\sin(\theta _{1}-\theta _{2})+g\sin(\theta _{2})=0\\(m_{1}+m_{2})l_{1}{\ddot {\theta }}_{1}+m_{2}l_{2}{\ddot {\theta }}_{2}\cos(\theta _{1}-\theta _{2})+m_{2}l_{2}{\dot {\theta }}_{2}^{2}\sin(\theta _{1}-\theta _{2})+(m_{1}+m_{2})g\sin(\theta _{1})=0\end{cases}}}
Ce sont les mêmes équations que pour l'approche lagrangienne.
Pendule à entraînement circulaire uniforme Un autre exercice classique concerne le cas où la première tige se meut d'un mouvement uniforme autour de son axe. On a alors θ 1 ˙ = ω {\displaystyle {\dot {\theta _{1}}}=\omega } θ 2 = θ {\displaystyle \theta _{2}=\theta \,}
l 2 θ ¨ = − l 1 ω 2 sin ( θ − ω t ) − g sin θ = − ( 1 + l 1 ω 2 g cos ω t ) g sin θ + l 1 ω 2 sin ω t cos θ {\displaystyle l_{2}{\ddot {\theta }}=-l_{1}\omega ^{2}\sin(\theta -\omega t)-g\sin \theta =-(1+{\frac {l_{1}\omega ^{2}}{g}}\cos \omega t)g\sin \theta +l_{1}\omega ^{2}\sin \omega t\cos \theta }
Pour de petites oscillations et l 1 ω 2 g << 1 {\displaystyle {\frac {l_{1}\omega ^{2}}{g}}<<1\,} l 2 θ ¨ + g θ = l 1 ω 2 sin ( ω t ) {\displaystyle l_{2}{\ddot {\theta }}+g\theta =l_{1}\omega ^{2}\sin(\omega t)} oscillateur harmonique forcé :
Mais si, dans ce cas, on choisit ω = g / l 2 {\displaystyle \omega ={\sqrt {g/l_{2}}}\,}
Notes et références
Voir aussi Liens externes L'article de scienceworld d'Eric Weisstein, en anglais Manipulation interactive du pendule double Vidéo : mouvement chaotique du double pendule Animation flash du botafumeiro Portail de la physique 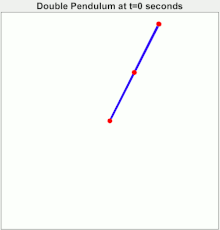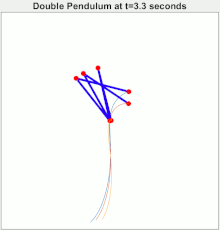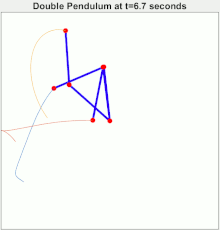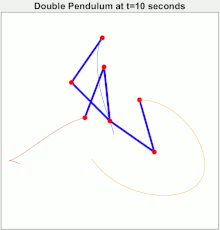



 Portail de la physique
Portail de la physique 





![{\displaystyle T={\frac {1}{2}}m_{1}v_{1}^{2}+{\frac {1}{2}}m_{2}v_{2}^{2}={\frac {1}{2}}m_{1}l_{1}^{2}{\dot {\theta }}_{1}^{2}+{\frac {1}{2}}m_{2}[l_{1}^{2}{\dot {\theta }}_{1}^{2}+l_{2}^{2}{\dot {\theta }}_{2}^{2}+2l_{1}l_{2}{\dot {\theta }}_{1}{\dot {\theta }}_{2}\cos(\theta _{1}-\theta _{2})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7073757e61f4d9b036fa221b288a48b440eb2e6c)

















































![{\displaystyle ={\frac {m_{2}[l_{1}(i{\ddot {\theta }}_{1}-{\dot {\theta }}_{1}^{2})(\cos \theta _{1}+i\sin \theta _{1})+l_{2}(i{\ddot {\theta }}_{2}-{\dot {\theta }}_{2}^{2})(\cos \theta _{2}+i\sin \theta _{2})]-m_{2}g-m_{1}g+m_{1}[l_{1}(i{\ddot {\theta }}_{1}-{\dot {\theta }}_{1}^{2})(\cos \theta _{1}+i\sin \theta _{1})]}{l_{1}\cos \theta _{1}+l_{1}i\sin \theta _{1}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3609a7fee57f3e4bbca35dbbd5bc71ca6e59d931)
![{\displaystyle ={\frac {m_{1}[l_{1}i{\ddot {\theta }}_{1}\cos \theta _{1}-l_{1}{\dot {\theta }}_{1}^{2}\cos \theta _{1}-l_{1}{\ddot {\theta }}_{1}\sin \theta _{1}-l_{1}i{\dot {\theta }}_{1}^{2}\sin \theta _{1}]-m_{1}g-m_{2}g}{l_{1}\cos \theta _{1}+l_{1}i\sin \theta _{1}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4931dc3625d298fda933c8825749628282868826)
![{\displaystyle +{\frac {m_{2}[l_{1}i{\ddot {\theta }}_{1}\cos \theta _{1}-l_{1}{\dot {\theta }}_{1}^{2}\cos \theta _{1}-l_{1}{\ddot {\theta }}_{1}\sin \theta _{1}-l_{1}i{\dot {\theta }}_{1}^{2}\sin \theta _{1}+l_{2}i{\ddot {\theta }}_{2}\cos \theta _{2}-l_{2}{\dot {\theta }}_{2}^{2}\cos \theta _{2}-l_{2}{\ddot {\theta }}_{2}\sin \theta _{2}-l_{2}i{\dot {\theta }}_{2}^{2}\sin \theta _{2}]}{l_{1}\cos \theta _{1}+l_{1}i\sin \theta _{1}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/15fab123eec0b163e6ef3f75238d8ef6b84949be)

![{\displaystyle [m_{1}(l_{1}i{\ddot {\theta }}_{1}\cos \theta _{1}-l_{1}i{\dot {\theta }}_{1}^{2}\sin \theta _{1})+m_{2}(l_{1}i{\ddot {\theta }}_{1}\cos \theta _{1}-l_{1}i{\dot {\theta }}_{1}^{2}\sin \theta _{1}+l_{2}i{\ddot {\theta }}_{2}\cos \theta _{2}-l_{2}i{\dot {\theta }}_{2}^{2}\sin \theta _{2})][\cos \theta _{1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/499742e18caed9187d9806f4399d367e3ebb832e)
![{\displaystyle +[m_{1}(-l_{1}{\dot {\theta }}_{1}^{2}\cos \theta _{1}-l_{1}{\ddot {\theta }}_{1}\sin \theta _{1})+m_{2}(-l_{1}{\dot {\theta }}_{1}^{2}\cos \theta _{1}-l_{1}{\ddot {\theta }}_{1}\sin \theta _{1}-l_{2}{\dot {\theta }}_{2}^{2}\cos \theta _{2}-l_{2}{\ddot {\theta }}_{2}\sin \theta _{2})-m_{1}g-m_{2}g][-i\sin \theta _{1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/638316eca7e8ce7ddaaea707b6629cc0a3d6afe9)






















