Grup kuaternion

Struktur aljabar → Teori grup Teori grup
Gagasan dasar Subgrup Subgrup normal Grup hasil bagi darab langsung semi-darab langsung Homomorfisme grup kernel bayangan jumlah langsung karangan bunga sederhana hingga takhingga kontinu multiplikatif aditif siklik Abel dihedral nilpoten terselesaikan aksi Glosarium teori grup Daftar topik teori grup
Grup hingga Klasifikasi grup sederhana hingga siklik bergantian tipe Lie sporadik Teorema Cauchy Teorema Lagrange Teorema Sylow Teorema Hall grup-p Grup Abel elementer Grup Frobenius Pengganda Schur Grup simetrik ${\displaystyle \mathrm {S} _{n}}$ Grup Klein ${\displaystyle \mathrm {V} }$ Grup dihedral ${\displaystyle \mathrm {D} _{n}}$ Grup kuaternion ${\displaystyle \mathrm {Q} }$ Grup disiklik ${\displaystyle \mathrm {Dic} _{n}}$
Grup diskret Kekisi Bilangan bulat (${\displaystyle \mathbb {Z} }$) Grup bebas Grup modular ${\displaystyle \mathrm {PSL} (2,\mathbb {Z} )}$ ${\displaystyle \mathrm {SL} (2,\mathbb {Z} )}$ Grup aritmetika Kekisi Grup hiperbolik
Topologis dan Grup Lie Solenoid Lingkaran Linear umum ${\displaystyle \mathrm {GL} (n)}$ Linear khusus ${\displaystyle \mathrm {SL} (n)}$ Ortogonal ${\displaystyle \mathrm {O} (n)}$ Euklides ${\displaystyle \mathrm {E} (n)}$ Ortogonal khusus ${\displaystyle \mathrm {SO} (n)}$ Uner ${\displaystyle \mathrm {U} (n)}$ Uniter khusus ${\displaystyle \mathrm {SU} (n)}$ Simplektik ${\displaystyle \mathrm {Sp} (n)}$ G2 F4 E6 E7 E8 Lorentz Poincaré konformal Difeomorfisme Gelung Grup Lie berdimensi takhingga ${\displaystyle O(\infty )}$ ${\displaystyle \mathrm {SU} (\infty )}$ ${\displaystyle \mathrm {Sp} (\infty )}$
Grup aljabar Grup aljabar linear Grup reduktif Varietas Abel Kurva eliptik
l b s

Dalam teori grup, grup angka empat Q₈ (terkadang hanya dilambangkan dengan Q) adalah grup non-abelian dari urutan delapan, isomorfik ke himpunan bagian delapan elemen ${\displaystyle \{1,i,j,k,-1,-i,-j,-k\}}$ dari angka empat di bawah perkalian. Ini diberikan oleh presentasi grup

${\displaystyle \mathrm {Q} _{8}=\langle {\bar {e}},i,j,k\mid {\bar {e}}^{2}=e,\;i^{2}=j^{2}=k^{2}=ijk={\bar {e}}\rangle ,}$

di mana e adalah elemen identitas dan e komutatif dengan elemen lain dalam grup.

Presentasi Q ₈ lainnya adalah:

${\displaystyle \mathrm {Q} _{8}=\langle a,b\mid a^{4}=\mathbf {1} ,a^{2}=b^{2},ba=a^{-1}b\rangle .}$

Dibandingkan dengan grup dihedral

Grup quaternion Q ₈ memiliki urutan yang sama dengan grup dihedral D₄, tetapi strukturnya berbeda, seperti yang ditunjukkan oleh grafik Cayley dan siklusnya:

	Q8	D4
Grafik Cayley	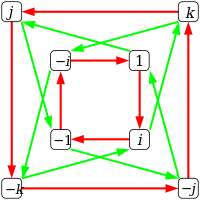Panah merah terhubung g→gi, koneksi hijau g→gj.
Grafik siklus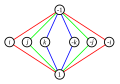

Dalam diagram untuk D ₄ , elemen grup ditandai dengan aksinya pada huruf F dalam representasi yang menentukan R². Hal yang sama tidak dapat dilakukan untuk Q ₈ , karena tidak memiliki representasi yang tepat di R² atau R³. D₄ dapat direalisasikan sebagai bagian dari pemmbagi angka empat dengan cara yang sama seperti Q ₈ dapat dilihat sebagai himpunan bagian dari angka empat.

Tabel Cayley

Tabel Cayley (tabel perkalian) untuk Q ₈ diberikan oleh:^[1]

×	e	e	i	i	j	j	k	k
e	e	e	i	i	j	j	k	k
e	e	e	i	i	j	j	k	k
i	i	i	e	e	k	k	j	j
i	i	i	e	e	k	k	j	j
j	j	j	k	k	e	e	i	i
j	j	j	k	k	e	e	i	i
k	k	k	j	j	i	i	e	e
k	k	k	j	j	i	i	e	e

Sifat

Perhatikan bahwa i , j , dan k semuanya memiliki urutan empat di Q ₈ dan dua di antaranya menghasilkan seluruh grup. Presentasi lainnya dari Q₈^[2] berdasarkan hanya dua elemen untuk melewati redundansi ini adalah:

${\displaystyle \langle x,y\mid x^{4}=1,x^{2}=y^{2},y^{-1}xy=x^{-1}\rangle .}$

Seseorang mungkin mengambil, misalnya, ${\displaystyle i=x,j=y}$, dan ${\displaystyle k=xy}$.

Grup quaternion memiliki properti yang tidak biasa sebagai Hamiltonian: Q₈ non-abelian, tetapi setiap subgrup adalah normal.^[3] Every Hamiltonian group contains a copy of Q₈.^[4]

Grup angka empat Q ₈ dan grup dihedral D ₄ adalah dua contoh terkecil dari grup non-abelian nilpoten.

Pusat dan subgrup komutator dari Q ₈ adalah subgrup ${\displaystyle \{e,{\bar {e}}\}}$. Grup automorfisme dalam dari Q ₈ diberikan oleh grup modulo pusatnya, yaitu grup faktor Q₈/{e,e}, untukmu isomorfik ke grup empat Klein V. Grup automorfisme dari Q ₈ adalah isomorfik sampai S ₄ , grup simetris pada empat huruf (lihat Representasi matriks di bawah), dan grup automorfisme luar dari Q ₈ adalah S₄/V, yang isomorfik ke S₃.

Grup angka empat Q ₈ memiliki lima kelas konjugasi, {e }, { e }, { i, i }, { j, j }, { k, k }, dan lima representasi tak tersederhanakan di atas bilangan kompleks, dengan dimensi 1,1,1,1,2:

Representasi trivial

Tanda tangani representasi dengan i, j, k-kernel: Q₈ memiliki tiga subgrup normal maksimal: subgrup siklik yang dihasilkan oleh i, j, dan k. Untuk setiap subkelompok normal maksimal N , kita mendapatkan representasi satu dimensi yang memfaktorkan melalui 2-elemen grup hasil bagi G/N. Representasi mengirimkan elemen N ke 1, dan elemen di luar N ke -1.

Representasi 2 dimensi: Dijelaskan di bawah dalam Representasi matriks .

Tabel karakter dari Q ₈ ternyata sama dengan D₄:

Representasi (ρ)/kelas konjugasi	{ e }	{ e }	{ i, i }	{ j, j }	{ k, k }
Representasi trivial	1	1	1	1	1
Tanda representasi dengan i-kernel	1	1	1	-1	-1
Tanda representasi dengan j-kernel	1	1	-1	1	-1
Tanda representasi dengan k-kernel	1	1	-1	-1	1
Representasi 2 dimensi	2	-2	0	0	0

Karena karakter yang tidak dapat direduksi ${\displaystyle \chi _{\rho }}$ pada baris di atas memiliki nilai riil, ini memberikan dekomposisi dari aljabar grup nyata dari ${\displaystyle G=Q_{8}}$ menjadi minimal dua sisi ideal: ${\displaystyle \textstyle \mathbb {R} [Q_{8}]\ =\ \bigoplus _{\rho }(e_{\rho })}$, di mana idempotensi ${\displaystyle e_{\rho }\in \mathbb {R} [Q_{8}]}$ sesuai dengan irreducibles: ${\displaystyle \textstyle e_{\rho }={\frac {\dim(\rho )}{|G|}}\sum _{g\in G}\chi _{\rho }(g^{-1})g}$, seperti

${\displaystyle e_{\text{triv}}={\tfrac {1}{8}}(e+{\bar {e}}+i+{\bar {i}}+j+{\bar {j}}+k+{\bar {k}})}$

${\displaystyle e_{i{\text{-ker}}}={\tfrac {1}{8}}(e+{\bar {e}}+i+{\bar {i}}-j-{\bar {j}}-k-{\bar {k}})}$

${\displaystyle e_{j{\text{-ker}}}={\tfrac {1}{8}}(e+{\bar {e}}-i-{\bar {i}}+j+{\bar {j}}-k-{\bar {k}})}$

${\displaystyle e_{k{\text{-ker}}}={\tfrac {1}{8}}(e+{\bar {e}}-i-{\bar {i}}-j-{\bar {j}}+k+{\bar {k}})}$

${\displaystyle e_{2}={\tfrac {2}{8}}(2e-2{\bar {e}})={\tfrac {1}{2}}(e-{\bar {e}})}$.

Masing-masing dari cita-cita tak tersederhanakan ini isomorfik ke aljabar sederhana pusat nyata, empat pertama ke bidang nyata ${\displaystyle \mathbb {R} }$. Ideal terakhir ${\displaystyle (e_{2})}$ isomorfik terhadap bidang miring dari angka empat ${\displaystyle \mathbb {H} }$ dengan korespondensi:

${\displaystyle \textstyle {\frac {1}{2}}(e-{\bar {e}})\longleftrightarrow 1,\ \ {\frac {1}{2}}(i-{\bar {i}})\longleftrightarrow i,\ \ {\frac {1}{2}}(j-{\bar {j}})\longleftrightarrow j,\ \ {\frac {1}{2}}(k-{\bar {k}})\longleftrightarrow k.}$

Selanjutnya, proyeksi homomorfisme ${\displaystyle \mathbb {R} [Q_{8}]\to (e_{2})\cong \mathbb {H} }$ diberikan oleh ${\displaystyle r\mapsto re_{2}}$ memiliki ideal kernel yang dihasilkan oleh idempoten:

${\displaystyle e_{2}^{\perp }\ =\ \textstyle e_{1}+e_{i{\text{-ker}}}+e_{j{\text{-ker}}}+e_{k{\text{-ker}}}\ =\ {\frac {1}{2}}(e+{\bar {e}}),}$

sehingga angka empat juga bisa diperoleh sebagai gelanggang hasil bagi ${\displaystyle \mathbb {R} [Q_{8}]/(e+{\bar {e}})\cong \mathbb {H} }$.

Aljabar grup kompleks dengan demikian ${\displaystyle \mathbb {C} [Q_{8}]\cong \mathbb {C} ^{\oplus 4}\oplus M_{2}(\mathbb {C} )}$, dimana ${\displaystyle M_{2}(\mathbb {C} )\cong \mathbb {H} \otimes _{\mathbb {R} }\!\mathbb {C} \cong \mathbb {H} \oplus \mathbb {H} }$ adalah aljabar dari bikuaternion.

Representasi matriks

Kompleks tak tersederhanakan dua dimensi representasi yang dijelaskan di atas memberikan grup kuatnion Q₈ sebagai subgrup dari grup linier umum ${\displaystyle \operatorname {GL} _{2}(\mathbb {C} )}$. Grup kuaternion adalah subgrup perkalian dari aljabar quaternion ${\displaystyle \mathbb {H} =\mathbb {R} 1+\mathbb {R} i+\mathbb {R} j+\mathbb {R} k=\mathbb {C} 1+\mathbb {C} j}$, yang memiliki representasi reguler ${\displaystyle \rho :\mathbb {H} \to \mathrm {M} _{2}(\mathbb {C} )}$ perkalian kiri dengan sendirinya dianggap sebagai ruang vektor kompleks dengan basis ${\displaystyle \{1,j\}}$, sehingga ${\displaystyle z\in \mathbb {H} }$ sesuai dengan C-pemetaan linier ${\displaystyle \rho _{z}:a{+}jb\mapsto z\cdot (a{+}jb)}$. Representasi yang dihasilkan ${\displaystyle \rho :\mathrm {Q} _{8}\to \mathrm {GL} _{2}(\mathbb {C} ),\ g\mapsto \rho _{g},}$ diberikan oleh:

${\displaystyle {\begin{matrix}e\mapsto {\begin{pmatrix}1&0\\0&1\end{pmatrix}}&i\mapsto {\begin{pmatrix}i&0\\0&-i\end{pmatrix}}&j\mapsto {\begin{pmatrix}0&-1\\1&0\end{pmatrix}}&k\mapsto {\begin{pmatrix}0&-i\\-i&0\end{pmatrix}}\\{\overline {e}}\mapsto {\begin{pmatrix}-1&0\\0&-1\end{pmatrix}}&{\overline {i}}\mapsto {\begin{pmatrix}-i&0\\0&i\end{pmatrix}}&{\overline {j}}\mapsto {\begin{pmatrix}0&1\\-1&0\end{pmatrix}}&{\overline {k}}\mapsto {\begin{pmatrix}0&i\\i&0\end{pmatrix}}.\end{matrix}}}$

Karena semua matriks di atas memiliki determinan unit, ini adalah representasi dari Q ₈ dalam grup linear khusus SL₂(C).^[5]

Varian memberikan representasi oleh matriks kesatuan (tabel di kanan). Maka ${\displaystyle g\in Q_{8}}$ sesuai dengan pemetaan linier ${\displaystyle \rho _{g}:a{+}bj\mapsto (a{+}bj)\cdot jg^{-1}j^{-1}}$, sehingga ${\displaystyle \rho :\mathrm {Q} _{8}\to \mathrm {SU} _{2}}$ diberikan oleh:

${\displaystyle {\begin{matrix}e\mapsto {\begin{pmatrix}1&0\\0&1\end{pmatrix}}&i\mapsto {\begin{pmatrix}i&0\\0&-i\end{pmatrix}}&j\mapsto {\begin{pmatrix}0&1\\-1&0\end{pmatrix}}&k\mapsto {\begin{pmatrix}0&i\\i&0\end{pmatrix}}\\{\overline {e}}\mapsto {\begin{pmatrix}-1&0\\0&-1\end{pmatrix}}&{\overline {i}}\mapsto {\begin{pmatrix}-i&0\\0&i\end{pmatrix}}&{\overline {j}}\mapsto {\begin{pmatrix}0&-1\\1&0\end{pmatrix}}&{\overline {k}}\mapsto {\begin{pmatrix}0&-i\\-i&0\end{pmatrix}}.\end{matrix}}}$

Ada juga tindakan penting Q ₈ pada ruang vektor 2 dimensi di atas bidang berhingga F₃ = {0,1,−1} (tabel di kanan). Representasi modular ${\displaystyle \rho :\mathrm {Q} _{8}\to \mathrm {SL} (2,3)}$ diberikan oleh

${\displaystyle {\begin{matrix}e\mapsto {\begin{pmatrix}1&0\\0&1\end{pmatrix}}&i\mapsto {\begin{pmatrix}1&1\\1&\!\!\!\!-1\end{pmatrix}}&j\mapsto {\begin{pmatrix}\!\!\!-1&1\\1&1\end{pmatrix}}&k\mapsto {\begin{pmatrix}0&\!\!\!\!-1\\1&0\end{pmatrix}}\\{\overline {e}}\mapsto {\begin{pmatrix}\!\!\!-1&0\\0&\!\!\!\!-1\end{pmatrix}}&{\overline {i}}\mapsto {\begin{pmatrix}\!\!\!-1&\!\!\!\!-1\\\!\!\!-1&1\end{pmatrix}}&{\overline {j}}\mapsto {\begin{pmatrix}1&\!\!\!\!-1\\\!\!\!-1&\!\!\!\!-1\end{pmatrix}}&{\overline {k}}\mapsto {\begin{pmatrix}0&1\\\!\!\!-1&0\end{pmatrix}}.\end{matrix}}}$

Representasi ini dapat diperoleh dari bidang ekstensi F₉ = F₃[k] = F₃1 + F₃k, dimana k² = −1 dan grup perkalian (F₉)^× memiliki generator ±(k+1), ±(k-1) urutan 8. Dua dimensi F₃-ruang vektor F₉ mengakui pemetaan linier ${\displaystyle \mu _{z}(a+bk)=z\cdot (a+bk)}$ untuk z pada F₉, serta Automorfisme Frobenius ${\displaystyle \phi (a+bk)=(a+bk)^{3}}$ satisfying ${\displaystyle \phi ^{2}=\mu _{1}}$ dan ${\displaystyle \phi \mu _{z}=\mu _{\phi (z)}\phi }$. Maka matriks representasi di atas adalah ${\displaystyle \rho ({\bar {e}})=\mu _{-1}}$, ${\displaystyle \rho (i)=\mu _{k+1}\phi }$, ${\displaystyle \rho (j)=\mu _{k-1}\phi }$, dan ${\displaystyle \rho (k)=\mu _{k}}$.

Grup Galois

Seperti yang ditunjukkan Richard Dean pada tahun 1981, grup kuaternion dapat ditampilkan sebagai grup Galois Gal(T/Q) dimana Q adalah bidang bilangan rasional dan T adalah bidang pemisah di atas Q dari polinomial

${\displaystyle x^{8}-72x^{6}+180x^{4}-144x^{2}+36}$.

Pengembangan menggunakan teorema fundamental teori Galois dalam menentukan empat bidang perantara antara Q dan T dan grup Galois mereka, serta dua teorema tentang ekstensi siklik derajat empat di atas bidang.^[6]

Grup angka empat digeneralisasi

Grup kuatnion umum Q_4n urutan 4n ditentukan oleh presentasi^[2]

${\displaystyle \langle x,y\mid x^{2n}=y^{4}=1,x^{n}=y^{2},y^{-1}xy=x^{-1}\rangle }$

untuk bilangan bulat n ≥ 2, dengan kelompok angka empat yang biasa diberikan oleh n = 2.^[7] Coxeter menggunakan Q_4n grup siklik ${\displaystyle \langle 2,2,n\rangle }$, kasus khusus dari grup polihedral biner ${\displaystyle \langle \ell ,m,n\rangle }$ dan terkait dengan grup polihedral ${\displaystyle (p,q,r)}$ dan grup dihedral ${\displaystyle (2,2,n)}$. Grup quaternion umum dapat direalisasikan sebagai subgrup ${\displaystyle \operatorname {GL} _{2}(\mathbb {C} )}$ dihasilkan oleh

${\displaystyle \left({\begin{array}{cc}\omega _{n}&0\\0&{\overline {\omega }}_{n}\end{array}}\right){\mbox{ and }}\left({\begin{array}{cc}0&-1\\1&0\end{array}}\right)}$

dimana ${\displaystyle \omega _{n}=e^{i\pi /n}}$.^[2] Ini juga dapat direalisasikan sebagai subgrup unit quaternions yang dihasilkan oleh^[8] ${\displaystyle x=e^{i\pi /n}}$ dan ${\displaystyle y=j}$.

Grup quaternion umum memiliki properti bahwa setiap subgrup abelian bersiklus.^[9] Dapat diperlihatkan bahwa p-group dengan properti ini (setiap subgrup abelian adalah siklik) bisa berupa siklik atau grup quaternion umum seperti yang didefinisikan di atas.^[10] Karakterisasi lain adalah bahwa sebuah grup p terbatas yang di dalamnya terdapat subgrup unik dari ordo p adalah siklik atau 2-grup isomorfik ke grup quaternion umum.^[11] Secara khusus, untuk bidang hingga F dengan karakteristik ganjil, subgrup 2-Sylow dari SL₂(F) non-abelian dan hanya memiliki satu subgrup orde 2, jadi subgrup 2-Sylow ini harus menjadi grup quaternion umum, (Gorenstein 1980, hlm. 42). Maka p^r menjadi ukuran F , di mana p adalah bilangan prima, ukuran subgrup 2-Sylow dari SL₂(F) adalah 2ⁿ, dimana n = ord₂(p² − 1) + ord₂(r).

Teorema Brauer–Suzuki menunjukkan bahwa grup yang subgrup Sylow 2-nya digeneralisasikan quaternion tidak bisa sederhana.

Terminologi lain mencadangkan nama "grup kuatnion umum" untuk kelompok siklik urutan pangkat 2,^[12] yang mengakui presentasi

${\displaystyle \langle x,y\mid x^{2^{m}}=y^{4}=1,x^{2^{m-1}}=y^{2},y^{-1}xy=x^{-1}\rangle .}$

Lihat pula

• sel-16
• Grup tetrahedral biner
• Aljabar Clifford
• Grup dikiklik
• Angka empat integral Hurwitz
• Daftar grup kecil

Catatan

Referensi

• Artin, Michael (1991), Algebra, Prentice Hall, ISBN 978-0-13-004763-2 
• Brown, Kenneth S. (1982), Cohomology of groups (edisi ke-3rd), Springer-Verlag, ISBN 978-0-387-90688-1 
• Cartan, Henri; Eilenberg, Samuel (1999), Homological Algebra, Princeton University Press, ISBN 978-0-691-04991-5 
• Coxeter, H. S. M.; Moser, W. O. J. (1980). Generators and Relations for Discrete Groups. New York: Springer-Verlag. ISBN 0-387-09212-9.  Parameter |name-list-style= yang tidak diketahui akan diabaikan (bantuan)
• Dean, Richard A. (1981) "A rational polynomial whose group is the quaternions", American Mathematical Monthly 88:42–5.
• Gorenstein, D. (1980), Finite Groups, New York: Chelsea, ISBN 978-0-8284-0301-6, MR 0569209 
• Johnson, David L. (1980), Topics in the theory of group presentations, Cambridge University Press, ISBN 978-0-521-23108-4, MR 0695161 
• Rotman, Joseph J. (1995), An introduction to the theory of groups (edisi ke-4th), Springer-Verlag, ISBN 978-0-387-94285-8 
• P.R. Girard (1984) "The quaternion group and modern physics", European Journal of Physics 5:25–32.
• Hall, Marshall (1999), The theory of groups (edisi ke-2nd), AMS Bookstore, ISBN 0-8218-1967-4 
• Kurosh, Alexander G. (1979), Theory of Groups, AMS Bookstore, ISBN 0-8284-0107-1 

Pranala luar

• (Inggris) Weisstein, Eric W. "Quaternion group". MathWorld. 
• Quaternion groups on GroupNames Diarsipkan 2023-08-09 di Wayback Machine.
• Quaternion group on GroupProps Diarsipkan 2023-05-14 di Wayback Machine.
• Conrad, Keith. "Generalized Quaternions" Diarsipkan 2023-06-02 di Wayback Machine.