Ruang Hilbert

Konsep matematika dari ruang Hilbert, dinamai David Hilbert, menggeneralisasi gagasan ruang Euklides. Maka memperluas metode aljabar vektor dan kalkulus dari dua dimensi bidang Euclidean dan ruang tiga dimensi ke ruang dengan berhingga atau tak hingga. Ruang Hilbert adalah ruang vektor yang dilengkapi dengan hasil kali dalam, sebuah operasi yang memungkinkan untuk menentukan panjang dan sudut. Lebih lanjut, ruang Hilbert adalah lengkap, yang berarti bahwa ada cukup limit di ruang untuk memungkinkan teknik kalkulus digunakan.

Ruang Hilbert muncul secara alami dan sering dalam matematika dan fisika, biasanya sebagai dimensi tak hingga ruang fungsi. Ruang Hilbert paling awal dipelajari dari sudut pandang ini pada dekade pertama abad ke-20 oleh David Hilbert, Erhard Schmidt, dan Frigyes Riesz. Mereka adalah alat yang sangat diperlukan dalam teori persamaan diferensial parsial s, mekanika kuantum, Analisis Fourier (yang mencakup aplikasi untuk pemrosesan sinyal dan perpindahan panas), dan teori ergodik (yang membentuk dasar matematika termodinamika). John von Neumann menciptakan istilah ruang Hilbert untuk konsep abstrak yang mendasari banyak aplikasi yang beragam ini. Keberhasilan metode ruang Hilbert mengantarkan era yang sangat bermanfaat bagi analisis fungsional. Terlepas dari ruang Euclidean klasik, contoh ruang Hilbert meliputi ruang fungsi terintegralkan persegi, ruang urutan, Ruang Sobolev terdiri dari fungsi umum, dan Ruang Hardy dari fungsi holomorfik.

Intuisi geometris memainkan peran penting dalam banyak aspek teori ruang Hilbert. Analog tepat dari Teorema Pythagoras dan hukum jajaran genjang berlaku di ruang Hilbert. Pada tingkat yang lebih dalam, proyeksi tegak lurus ke subruang (analog dari "menurunkan ketinggian" dari segitiga) memainkan peran penting dalam masalah pengoptimalan dan lainnya sebagai. Sebuah elemen ruang Hilbert dapat secara unik ditentukan oleh koordinatnya sehubungan dengan satu set sumbu koordinat (sebuah basis orthonormal), dalam analogi dengan koordinat Kartesius pada bidang. Ketika himpunan sumbu itu countably infinite, ruang Hilbert juga dapat dianggap berguna dalam hal ruang urutan tak hingga yang persegi summabel. Ruang terakhir sering dalam literatur yang lebih tua disebut sebagai ruang Hilbert. Operator linear pada ruang Hilbert juga merupakan objek yang cukup konkret: dalam kasus yang baik, mereka hanyalah transformasi yang meregangkan ruang oleh faktor-faktor berbeda dalam arah yang saling tegak lurus dalam arti yang dibuat tepat oleh studi spektrum.

Definisi dan ilustrasi

Contoh motivasi: Ruang vektor Euklides

Salah satu contoh paling umum dari ruang Hilbert adalah ruang vektor Euklides yang terdiri dari vektor tiga dimensi, dilambangkan dengan ℝ³, dan dilengkapi dengan dot product. Perkalian titik mengambil dua vektor x dan y, dan menghasilkan bilangan riil x · y. Jika x dan y direpresentasikan dalam koordinat kartesius, kemudian perkalian titik didefinisikan oleh

${\displaystyle {\begin{pmatrix}x_{1}\\x_{2}\\x_{3}\end{pmatrix}}\cdot {\begin{pmatrix}y_{1}\\y_{2}\\y_{3}\end{pmatrix}}=x_{1}y_{1}+x_{2}y_{2}+x_{3}y_{3}\,.}$

Produk titik memenuhi sifat:

1. Simetri dalam x dan y: x · y = y · x.
2. Linear dalam argumen pertamanya: (ax₁ + bx₂) · y = ax₁ · y + bx₂ · y untuk semua skalar a, b, dan vektor x₁, x₂, dan y.
3. Bentuk positif: untuk semua vektor x, x · x ≥ 0 , dengan kesetaraan jika dan hanya jika x = 0.

Operasi pada pasangan vektor yang, seperti perkalian titik, memenuhi ketiga sifat ini dikenal sebagai (riil) hasil kali dalam. Sebuah ruang vektor yang dilengkapi dengan hasil kali dalam seperti itu dikenal sebagai ruang hasil kali dalam. Setiap ruang hasilkali dalam berdimensi-hingga juga merupakan ruang Hilbert. Fitur dasar dari perkalian titik yang menghubungkannya dengan geometri Euclidean adalah bahwa ia terkait dengan panjang (atau norma) vektor, dilambangkan Templat:Norm, dan untuk sudut θ antara dua vektor x dan y melalui rumus

${\displaystyle \mathbf {x} \cdot \mathbf {y} =\|\mathbf {x} \|\,\|\mathbf {y} \|\,\cos \theta \,.}$

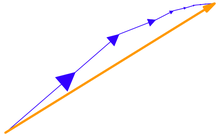
Kalkulus multivariabel dalam ruang Euklides bergantung pada kemampuan untuk menghitung limit, dan memiliki kriteria yang berguna pada deret matematika

${\displaystyle \sum _{n=0}^{\infty }\mathbf {x} _{n}}$

terdiri dari vektor dalam ℝ³ adalah konvergensi absolut asalkan jumlah panjangnya konvergen sebagai rangkaian bilangan riil biasa:^[1]

${\displaystyle \sum _{k=0}^{\infty }\|\mathbf {x} _{k}\|<\infty \,.}$

Sama seperti deret skalar, deret vektor yang bertemu secara mutlak juga konvergen ke beberapa vektor batas L di ruang Euklides, dalam arti bahwa

${\displaystyle \left\|\mathbf {L} -\sum _{k=0}^{N}\mathbf {x} _{k}\right\|\to \mathbf {0} \quad {\text{as }}N\to \infty \,.}$

Properti ini mengungkapkan kelengkapan ruang Euclidean: bahwa rangkaian yang menyatu secara mutlak juga menyatu dalam pengertian biasa.

Spasi Hilbert sering kali diambil alih dari bilangan kompleks. Bidang kompleks yang dilambangkan dengan ℂ dilengkapi dengan gagasan besaran, modulus kompleks |z| yang didefinisikan sebagai akar kuadrat dari hasil kali z dengan konjugasi kompleks:

${\displaystyle |z|^{2}=z{\overline {z}}\,.}$

Jika z = x + iy adalah dekomposisi dari z menjadi bagian nyata dan imajinernya, maka modulusnya adalah panjang dua dimensi Euklides yang biasa:

${\displaystyle |z|={\sqrt {x^{2}+y^{2}}}\,.}$

Hasil kali dalam dari pasangan bilangan kompleks z dan w adalah hasil kali dari z dengan konjugasi kompleks dari w:

${\displaystyle \langle z,w\rangle =z{\overline {w}}\,.}$

Ini bernilai kompleks. Bagian riil dari ⟨z, w⟩ memberikan Euclidean dua dimensi biasa perkalian titik.

Contoh kedua adalah ruang ℂ² yang elemennya adalah pasangan bilangan kompleks z = (z₁, z₂). Kemudian hasil kali dalam dari z dengan vektor lain w = (w₁, w₂) dirumuskan

${\displaystyle \langle z,w\rangle =z_{1}{\overline {w_{1}}}+z_{2}{\overline {w_{2}}}\,.}$

Bagian riil dari ⟨z, w⟩ kemudian adalah perkalian titik Euclidean dua dimensi. Hasil kali dalam ini simetris Hermitian , yang berarti hasil pertukaran z dan w adalah konjugat kompleks:

${\displaystyle \langle w,z\rangle ={\overline {\langle z,w\rangle }}\,.}$

Definisi

Ruang Hilbert H adalah riil atau kompleks hasil kali dalam yang juga merupakan ruang metrik lengkap sehubungan dengan fungsi jarak yang diinduksi oleh hasil kali dalam.^[2]

Mengatakan bahwa H adalah ruang hasil kali dalam kompleks H adalah ruang vektor kompleks yang di dalamnya terdapat bagian dalam produk ⟨x, y⟩ mengaitkan bilangan kompleks ke setiap pasangan elemen x , y dari H yang memenuhi properti berikut:

1. Hasil kali dalam adalah simetris konjugasi; yaitu, hasil kali dalam dari sepasang elemen sama dengan konjugasi kompleks dari produk dalam dari elemen yang ditukar:

   ${\displaystyle \langle y,x\rangle ={\overline {\langle x,y\rangle }}\,.}$

2. Hasil kali dalam adalah linier pada awalnya^{[nb 1]} argumen. Untuk bilangan kompleks a dan b ,

   ${\displaystyle \langle ax_{1}+bx_{2},y\rangle =a\langle x_{1},y\rangle +b\langle x_{2},y\rangle \,.}$

   ${\displaystyle {\begin{cases}\langle x,x\rangle >0&x\neq 0\\\langle x,x\rangle =0&x=0\,.\end{cases}}}$

Ini mengikuti dari properti 1 dan 2 bahwa produk dalam kompleks adalah antilinear, juga disebut konjugasi linear, dalam argumen keduanya, yang berarti bahwa

${\displaystyle \langle x,ay_{1}+by_{2}\rangle ={\bar {a}}\langle x,y_{1}\rangle +{\bar {b}}\langle x,y_{2}\rangle \,.}$

Ruang perkalian dalam riil didefinisikan dengan cara yang sama, kecuali bahwa H adalah ruang vektor nyata dan hasil kali dalam mengambil bilangan riil. Produk dalam seperti itu adalah peta bilinear dan (H, H, ⟨ ⋅, ⋅⟩) akan membentuk sistem ganda.^[3]

norma adalah fungsi nilai riil

${\displaystyle \|x\|={\sqrt {\langle x,x\rangle }}\,,}$

dan jarak d antara dua titik x , y di H didefinisikan dalam istilah dari norma oleh

${\displaystyle d(x,y)=\|x-y\|={\sqrt {\langle x-y,x-y\rangle }}\,.}$

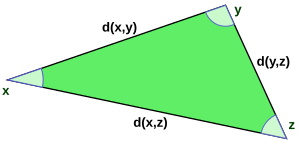
Bahwa fungsi ini adalah fungsi jarak, pertama-tama fungsi ini simetris dalam x dan y , kedua jarak antara x dan itu sendiri nol, dan sebaliknya jarak antara x dan y harus positif, dan terakhir pertidaksamaan segitiga tahan, artinya panjang salah satu kaki segitiga xyz tidak boleh melebihi jumlah panjang kedua kaki lainnya:

${\displaystyle d(x,z)\leq d(x,y)+d(y,z)\,.}$

Properti terakhir ini pada akhirnya merupakan konsekuensi dari pertidaksamaan Cauchy–Schwarz yang lebih mendasar, yang menegaskan

${\displaystyle {\bigl |}\langle x,y\rangle {\bigr |}\leq \|x\|\,\|y\|}$

dengan persamaan jika dan hanya jika x dan y adalah dependen linear.

Dengan fungsi jarak yang ditentukan dengan cara ini, setiap hasil kali dalam adalah ruang metrik, dan terkadang dikenal sebagai ruang Hausdorff.^[4] Setiap ruang pra-Hilbert yang juga merupakan ruang kompleks adalah ruang Hilbert.

kelengkapan dari H diekspresikan menggunakan bentuk Kriteria Cauchy untuk urutan dalam H : ruang pra-Hilbert H selesai jika setiap urutan Cauchy menyatu sehubungan dengan norma ini ke elemen dalam ruang. Kelengkapan dapat dicirikan oleh kondisi ekivalen berikut: jika serangkaian vektor

${\displaystyle \sum _{k=0}^{\infty }u_{k}}$

menyatu secara mutlak dalam arti itu

${\displaystyle \sum _{k=0}^{\infty }\|u_{k}\|<\infty \,,}$

kemudian deret tersebut menyatu di H , dalam arti bahwa jumlah parsial menyatu ke elemen H .

Contoh kedua: ruang urutan

Ruang urutan l ² terdiri dari semua urutan tak hingga z = (z₁, z₂, …) dari bilangan kompleks sehingga deret

${\displaystyle \sum _{n=1}^{\infty }|z_{n}|^{2}}$

menyatu. Produk bagian dalam aktif l² didefinisikan oleh

${\displaystyle \langle \mathbf {z} ,\mathbf {w} \rangle =\sum _{n=1}^{\infty }z_{n}{\overline {w_{n}}}\,,}$

dengan seri terakhir berkumpul sebagai konsekuensi dari pertidaksamaan Cauchy–Schwarz.

Kelengkapan ruang yang dipegang asalkan sederet elemennya berasal l² konvergen mutlak (dalam norma), lalu menyatu ke elemen l². Buktinya adalah dasar dalam analisis matematis, dan memungkinkan deret matematika elemen ruang untuk dimanipulasi dengan kemudahan yang sama seperti deret bilangan kompleks (atau vektor hingga).^[5]

Sejarah

Sebelum pengembangan ruang Hilbert, generalisasi lain dari ruang Euklides diketahui matematikawan dan fisikawan. Secara khusus, gagasan tentang ruang linier abstrak (ruang vektor) telah mendapatkan daya tarik menjelang akhir abad ke-19:^[6] ini adalah ruang yang elemen-elemennya dapat dijumlahkan dan dikalikan dengan skalar (riil atau bilangan kompleks) tanpa perlu mengidentifikasi elemen-elemen ini dengan vektor "geometris", seperti vektor posisi dan momentum dalam sistem fisik. Objek lain yang dipelajari oleh ahli matematika pada pergantian abad ke-20, dalam ruang tertentu urutan (termasuk deret) dan ruang fungsi,^[7] secara alami dapat dianggap sebagai ruang linier. Fungsi, misalnya, dapat ditambahkan atau dikalikan dengan skalar konstan, dan operasi ini mematuhi hukum aljabar yang dipenuhi oleh penjumlahan dan perkalian skalar dari vektor spasial.

Pada dekade pertama abad ke-20, perkembangan paralel mengarah pada pengenalan ruang Hilbert. Yang pertama adalah pengamatan, yang muncul selama David Hilbert dan Erhard Schmidt mempelajari persamaan integral,^[8] bahwa dua fungsi bernilai nyata square-integrable f dan g pada interval [a, b] memiliki produk dalam

${\displaystyle \langle f,g\rangle =\int _{a}^{b}f(x)g(x)\,\mathrm {d} x}$

yang memiliki banyak sifat familiar dari perkalian titik Euklides. Secara khusus, gagasan tentang keluarga fungsi ortogonal memiliki makna. Schmidt mengeksploitasi kemiripan hasil kali dalam ini dengan hasil kali titik biasa untuk membuktikan analog dari dekomposisi spektral untuk operator bentuk

${\displaystyle f(x)\mapsto \int _{a}^{b}K(x,y)f(y)\,\mathrm {d} y}$

di mana K adalah fungsi kontinu yang simetris di x dan y. Perluasan fungsi eigen yang dihasilkan menyatakan fungsi K sebagai rangkaian bentuk

${\displaystyle K(x,y)=\sum _{n}\lambda _{n}\varphi _{n}(x)\varphi _{n}(y)}$

dimana fungsi φ_n ortogonal dalam arti bahwa ⟨φ_nφ_m⟩ = 0 maka n ≠ m. Istilah individu dalam seri ini terkadang disebut sebagai solusi produk dasar. Namun, ada perluasan fungsi eigen yang gagal untuk menyatu dalam arti yang sesuai ke fungsi yang dapat diintegrasikan persegi: bahan yang hilang, yang memastikan konvergensi, adalah kelengkapan.^[9]

Perkembangan kedua adalah integral Lebesgue, alternatif dari integral Riemann yang diperkenalkan oleh Henri Lebesgue pada tahun 1904.^[10] Integral Lebesgue memungkinkan untuk mengintegrasikan kelas fungsi yang lebih luas. Pada tahun 1907, Frigyes Riesz dan Ernst Sigismund Fischer secara independen membuktikan bahwa ruang L² of fungsi terintegralkan Lebesgue persegi adalah ruang metrik komplek.^[11] Sebagai konsekuensi dari interaksi antara geometri dan kelengkapan, hasil abad ke-19 Joseph Fourier, Friedrich Bessel dan Marc-Antoine Parseval pada deret trigonometri dengan mudah dibawa ke ruang yang lebih umum ini, menghasilkan aparatus geometris dan analitik yang sekarang biasanya dikenal sebagai teorema Riesz–Fischer.^[12]

Hasil dasar lebih lanjut dibuktikan pada awal abad ke-20. Misalnya, Teorema representasi Riesz secara independen ditetapkan oleh Maurice Fréchet dan Frigyes Riesz pada tahun 1907.^[13] John von Neumann menciptakan istilah ruang Hilbert abstrak dalam karyanya pada Operator Hermitian.^[14] Meskipun ahli matematika lain seperti Hermann Weyl dan Norbert Wiener telah mempelajari ruang Hilbert tertentu dengan sangat rinci, sering kali dari sudut pandang motivasi fisik, von Neumann memberikan perlakuan pertama yang lengkap dan aksiomatik terhadap mereka.^[15] Von Neumann kemudian menggunakannya dalam pekerjaan penting tentang dasar-dasar mekanika kuantum,^[16] dan terus bekerja dengan Eugene Wigner. Nama "ruang Hilbert" segera diadopsi oleh orang lain, misalnya oleh Hermann Weyl dalam bukunya tentang mekanika kuantum dan teori grup.^[17]

Signifikansi konsep ruang Hilbert digarisbawahi dengan kesadaran bahwa ia menawarkan salah satu formulasi matematis kuantitatif^[18] Singkatnya, status sistem mekanik kuantum adalah vektor di ruang Hilbert tertentu, yang dapat diamati adalah operator pertapa di ruang tersebut, kesimetrian dari sistem adalah operator kesatuan s, dan pengukuran adalah proyeksi ortogonal. Hubungan antara kesimetrian mekanika kuantum dan operator kesatuan memberikan dorongan untuk pengembangan kesatuan teori representasi dari grup dimulai pada tahun 1928 karya Hermann Weyl.^[17] Di sisi lain, pada awal tahun 1930-an menjadi jelas bahwa mekanika klasik dapat dijelaskan dalam istilah ruang Hilbert (Mekanika klasik Koopman-von Neumann) dan beberapa sifat klasik sistem dinamis dapat dianalisis menggunakan teknik ruang Hilbert dalam kerangka teori ergodik.^[19]

Aljabar teramati dalam mekanika kuantum secara alami adalah aljabar operator yang ditentukan pada ruang Hilbert, menurut formulasi mekanika matriks kuantum th Werner Heisenberg Von Neumann mulai menyelidiki operator aljabar pada tahun 1930-an, sebagai gelanggang operator di ruang Hilbert. Jenis aljabar yang dipelajari oleh von Neumann dan orang-orang sezamannya sekarang dikenal sebagai aljabar Von Neumann. Pada tahun 1940-an, Israel Gelfand, Mark Naimark dan Irving Segal memberikan definisi sejenis aljabar operator yang disebut C*-aljabar yang di satu sisi tidak referensi ke yang mendasari dan di sisi lain mengekstrapolasi banyak fitur berguna dari aljabar operator yang sebelumnya telah dipelajari. Teorema spektral untuk operator self-adjoint khususnya yang mendasari banyak teori ruang Hilbert yang ada digeneralisasikan menjadi C*-aljabar. Teknik-teknik ini sekarang menjadi dasar dalam analisis harmonik abstrak dan teori representasi.

Pelengkap dan proyeksi ortogonal

Jika S adalah himpunan bagian dari spasi Hilbert H , himpunan vektor ortogonal ke S didefinisikan oleh

${\displaystyle S^{\perp }=\left\{x\in H:\langle x,s\rangle =0\ \forall s\in S\right\}\,.}$

S^⊥ adalah subruang tertutup dari H (dapat dibuktikan dengan mudah menggunakan linearitas dan kontinuitas hasil kali dalam) sehingga membentuk ruang Hilbert sendiri. Jika V adalah subruang tertutup dari H , maka V^⊥ disebut pelengkap ortogonal dari V . Faktanya, setiap x ∈ H kemudian dapat ditulis secara unik sebagai x = v + w, dengan v ∈ V dan w ∈ V^⊥. Oleh karena itu, H adalah penjumlahan internal Hilbert dari V dan V^⊥.

Operator linear P_V : H → H yang memetakan x ke v disebut proyeksi ortogonal ke V . Ada korespondensi satu-ke-satu natural antara himpunan semua subruang tertutup dari H dan himpunan semua operator adjoint mandiri yang dibatasi P dirumuskan P² = P.

Maka hal ini memberikan interpretasi geometris dari P_V(x): itu adalah perkiraan terbaik untuk x dengan elemen V .^[20]

Proyeksi P_U dan P_V disebut saling ortogonal jika P_UP_V = 0. Ini setara dengan U dan V ortogonal sebagai subruang dari H . Jumlah dari dua proyeksi P_U dan P_V adalah proyeksi hanya jika U dan V ortogonal satu sama lain, dan dalam hal itu P_U + P_V = P_U+V. Komposit P_UP_V umumnya bukan proyeksi; pada kenyataannya, komposit adalah proyeksi jika dan hanya jika dua proyeksi tersebut berpindah-pindah, dan dalam kasus P_UP_V = P_U∩V.

Dengan membatasi codomain ke ruang Hilbert V , proyeksi ortogonal P_V memunculkan pemetaan proyeksi π : H → V; itu adalah ujung dari pemetaan inklusi

${\displaystyle i:V\to H\,,}$

yang berarti bahwa

${\displaystyle \left\langle ix,y\right\rangle _{H}=\left\langle x,\pi y\right\rangle _{V}}$

pada x ∈ V dan y ∈ H.

Norma operator dari proyeksi ortogonal P_V ke subruang tertutup bukan nol V sama dengan 1:

${\displaystyle \|P_{V}\|=\sup _{x\in H,x\not =0}{\frac {\|P_{V}x\|}{\|x\|}}=1\,.}$

Oleh karena itu, setiap subruang tertutup V dari ruang Hilbert adalah citra operator P dari norma satu sehingga P² = P. Properti memiliki operator proyeksi yang sesuai menjadi ciri ruang Hilbert:^[21]

• Ruang Banach dengan dimensi lebih tinggi dari 2 adalah (secara isometrik) ruang Hilbert jika dan hanya jika, untuk setiap subruang tertutup V , terdapat operator P_V dari norma satu yang citranya adalah V maka P2V = P_V.

Sementara hasil ini mencirikan struktur metrik ruang Hilbert, struktur ruang Hilbert sebagai ruang vektor topologis itu sendiri dapat dicirikan dalam hal keberadaan komponen:^[22]

• Spasi Banach X secara topologi dan linier isomorfik ke ruang Hilbert jika dan hanya jika, untuk setiap subruang tertutup V , ada subruang tertutup W sedemikian rupa sehingga X sama dengan jumlah langsung internal V ⊕ W.

Pelengkap ortogonal memenuhi beberapa hasil yang lebih mendasar. Ini adalah fungsi monoton dalam arti jika U ⊂ V, kemudian V^⊥ ⊆ U^⊥ dengan kepemilikan persamaan jika dan hanya jika V terdapat dalam penutupan dari U . Hasil ini adalah kasus khusus dari Teorema Hahn–Banach. Penutupan subruang dapat sepenuhnya dicirikan dalam istilah komplemen ortogonal: jika V adalah subruang dari H , maka penutupan dari V sama dengan V^⊥⊥. Jadi, komplemen ortogonal adalah koneksi Galois pada urutan parsial dari subruang ruang Hilbert. Secara umum, komplemen ortogonal dari sejumlah subruang adalah perpotongan dari komplemen:^[23]

${\displaystyle \left(\sum _{i}V_{i}\right)^{\perp }=\bigcap _{i}V_{i}^{\perp }\,.}$

Jika V_i juga ditutup, maka

${\displaystyle {\overline {\sum _{i}V_{i}^{\perp }}}=\left(\bigcap _{i}V_{i}\right)^{\perp }\,.}$

Teori spektral

Ada teori spektral yang dikembangkan dengan baik untuk operator self-adjoint di ruang Hilbert, yang secara kasar dapat dianalogikan dengan studi matriks simetris pada real atau matriks adjoint sendiri pada bilangan kompleks.^[24] Dalam pengertian yang sama, seseorang dapat memperoleh "diagonalisasi" dari operator adjoint sendiri sebagai jumlah yang sesuai (sebenarnya merupakan integral) dari operator proyeksi ortogonal.

Spektrum operator T , dilambangkan dengan σ(T), adalah himpunan bilangan kompleks λ sedemikian rupa sehingga T − λ tidak memiliki pembalikan terus menerus. Jika T dibatasi, maka spektrum selalu merupakan himpunan kompak dalam bidang kompleks, dan terletak di dalam cakram |z| ≤ Templat:Norm. Jika T adalah self-adjoint, maka spektrumnya nyata. Faktanya, itu terkandung dalam interval [m, M] dimana

${\displaystyle m=\inf _{\|x\|=1}\langle Tx,x\rangle \,,\quad M=\sup _{\|x\|=1}\langle Tx,x\rangle \,.}$

Selain itu, m dan M keduanya sebenarnya berada dalam spektrum.

Eigenpaces dari operator T dirumuskan

${\displaystyle H_{\lambda }=\ker(T-\lambda )\,.}$

Tidak seperti matriks berhingga, tidak setiap elemen spektrum T harus berupa nilai eigen: operator linear T − λ mungkin hanya kekurangan invers karena tidak surjective. Elemen spektrum operator dalam pengertian umum dikenal sebagai nilai spektral . Karena nilai spektral tidak harus berupa nilai eigen, dekomposisi spektral sering kali lebih halus daripada dalam dimensi yang terbatas.

Namun, teorema spektral dari operator adjoint sendiri T mengambil bentuk yang sangat sederhana jika, sebagai tambahan, T diasumsikan jadilah operator kompak. teorema spektral untuk operator adjoint kompak menyatakan:^[25]

• Operator adjoint mandiri yang ringkas T hanya memiliki banyak nilai spektral yang terhitung (atau tak terbatas). Spektrum T tidak memiliki titik batas dalam bidang kompleks kecuali mungkin nol. Eigenpaces dari T menguraikan H menjadi jumlah langsung ortogonal:

  ${\displaystyle H=\bigoplus _{\lambda \in \sigma (T)}H_{\lambda }\,.}$

jika E_λ menunjukkan proyeksi ortogonal ke ruang eigen H_λ, then

${\displaystyle T=\sum _{\lambda \in \sigma (T)}\lambda E_{\lambda }\,,}$

di mana jumlah tersebut menyatu sehubungan dengan norma di B(H).

Teorema ini memainkan peran fundamental dalam teori persamaan integral, karena banyak operator integral kompak, khususnya yang muncul dari operator Hilbert–Schmidt.

Teorema spektral umum untuk operator self-adjoint melibatkan semacam operator bernilai integral Riemann–Stieltjes, daripada penjumlahan tak terbatas.^[26] Keluarga spektral yang terkait dengan T terkait dengan setiap bilangan riil λ sebuah operator E_λ, yang merupakan proyeksi ke ruang null operator (T − λ)⁺, dengan bagian positif dari operator adjoint ditentukan oleh

${\displaystyle A^{+}={\tfrac {1}{2}}\left({\sqrt {A^{2}}}+A\right)\,.}$

Operator E_λ Apakah monoton meningkat relatif terhadap urutan parsial yang ditentukan pada operator adjoint sendiri; nilai eigen sama persis dengan diskontinuitas lompatan. Seseorang memiliki teorema spektral, yang menegaskan

${\displaystyle T=\int _{\mathbb {R} }\lambda \,\mathrm {d} E_{\lambda }\,.}$

Integral dipahami sebagai integral Riemann–Stieltjes, konvergen sehubungan dengan norma di B(H). Secara khusus, seseorang memiliki representasi integral nilai skalar biasa

${\displaystyle \langle Tx,y\rangle =\int _{\mathbb {R} }\lambda \,\mathrm {d} \langle E_{\lambda }x,y\rangle \,.}$

Dekomposisi spektral yang agak mirip berlaku untuk operator normal, meskipun karena spektrum sekarang mungkin berisi bilangan kompleks non-nyata, ukuran Stieltjes yang dihargai operator dE_λ sebagai gantinya harus diganti dengan resolusi identitas.

Aplikasi utama dari metode spektral adalah teorema pemetaan spektral, yang memungkinkan seseorang untuk diterapkan ke operator adjoint mandiri T fungsi kompleks berkelanjutan apa pun f yang ditentukan pada spektrum T ' ' dengan membentuk integral

${\displaystyle f(T)=\int _{\sigma (T)}f(\lambda )\,\mathrm {d} E_{\lambda }\,.}$

Kalkulus fungsional berkelanjutan yang dihasilkan memiliki aplikasi khususnya untuk operator pseudodiferensial.^[27]

Teori spektral operator self-adjoint tidak terbatas hanya sedikit lebih sulit daripada operator terikat. Spektrum operator tak terbatas didefinisikan dengan cara yang persis sama: λ adalah nilai spektral jika operator penyelesai

${\displaystyle R_{\lambda }=(T-\lambda )^{-1}}$

gagal menjadi operator berkelanjutan yang terdefinisi dengan baik. Penyesuaian diri T masih menjamin bahwa spektrumnya riil. Dengan demikian, gagasan penting untuk bekerja dengan operator tak terbatas adalah untuk melihat resolvent R_λ dimana λ tidak nyata. Ini adalah operator normal terbatas , yang mengakui representasi spektral yang kemudian dapat ditransfer ke representasi spektral dari T . Strategi serupa digunakan, misalnya, untuk mempelajari spektrum operator Laplace: daripada menangani operator secara langsung, seseorang malah terlihat sebagai resolvent terkait.

Versi tepat dari teorema spektral dalam kasus ini adalah:^[28]

Diketahui operator adjoint mandiri yang didefinisikan secara padat T pada spasi Hilbert H , terdapat kesamaan resolusi identitas E pada himpunan Borel

${\displaystyle \langle Tx,y\rangle =\int _{\mathbb {R} }\lambda \,\mathrm {d} E_{x,y}(\lambda )}$

pada x ∈ D(T) and y ∈ H. Ukuran spektral E terkonsentrasi pada spektrum T .

Ada juga versi teorema spektral yang berlaku untuk operator normal tak terbatas.

Dalam budaya populer

Thomas Pynchon memperkenalkan karakter fiksi, Sammy Hilbert-Spaess (plesetan dari "ruang Hilbert"), dalam novel tahun 1973, Gravity's Rainbow. Hilbert-Spaess pertama kali digambarkan sebagai "agen ganda di mana-mana" dan kemudian sebagai "setidaknya agen ganda".^[29] Novel tersebut sebelumnya telah mereferensikan karya sesama matematikawan Jerman Kurt Gödel Teorema Ketidaklengkapan,^[30] yang menunjukkan bahwa Program Hilbert, rencana formal Hilbert untuk menyatukan matematika menjadi satu set aksioma, tidak mungkin.^[31]

Lihat pula

• Ruang Banach – ruang vektor dengan metrik yang memungkinkan penghitungan panjang vektor dan jarak antara vektor dan lengkap dalam arti bahwa urutan Cauchy vektor selalu konvergen ke batas yang didefinisikan dengan baik yang ada di dalam ruang
• Teorema dasar ruang Hilbert – metode aljabar vektor dan kalkulus dari dua dimensi bidang Euclidean dan ruang tiga dimensi ke ruang dengan berhingga atau tak hingga
• Ruang Hadamard – metode aljabar vektor dan kalkulus dari dua dimensi bidang Euclidean dan ruang tiga dimensi ke ruang dengan berhingga atau tak hingga
• Aljabar Hilbert – metode aljabar vektor dan kalkulus dari dua dimensi bidang Euclidean dan ruang tiga dimensi ke ruang dengan berhingga atau tak hingga
• Hilbert modul-C* – metode aljabar vektor dan kalkulus dari dua dimensi bidang Euclidean dan ruang tiga dimensi ke ruang dengan berhingga atau tak hingga
• lipatan Hilbert – metode aljabar vektor dan kalkulus dari dua dimensi bidang Euclidean dan ruang tiga dimensi ke ruang dengan berhingga atau tak hingga
• Produk L-semi-dalam – metode aljabar vektor dan kalkulus dari dua dimensi bidang Euclidean dan ruang tiga dimensi ke ruang dengan berhingga atau tak hingga
• Ruang vektor topologis konveks lokal – metode aljabar vektor dan kalkulus dari dua dimensi bidang Euclidean dan ruang tiga dimensi ke ruang dengan berhingga atau tak hingga
• Teori operator – metode aljabar vektor dan kalkulus dari dua dimensi bidang Euclidean dan ruang tiga dimensi ke ruang dengan berhingga atau tak hingga
• Topologi operator – metode aljabar vektor dan kalkulus dari dua dimensi bidang Euclidean dan ruang tiga dimensi ke ruang dengan berhingga atau tak hingga
• Rijet ruang Hilbert – metode aljabar vektor dan kalkulus dari dua dimensi bidang Euclidean dan ruang tiga dimensi ke ruang dengan berhingga atau tak hingga
• Ruang vektor topologis – salah satu struktur dasar yang diteliti dalam analisis fungsional

Catatan

Keterangan

Kutipan

Referensi

Pranala luar