 標準アステロイド
標準アステロイド  内擺線としてのアステロイド
内擺線としてのアステロイド  楕円族の包絡線としてのアステロイド
楕円族の包絡線としてのアステロイド 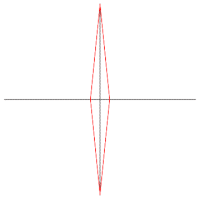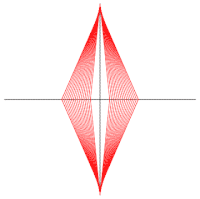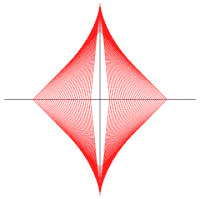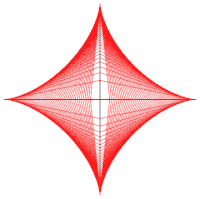 線分の包絡線としてのアステロイド
線分の包絡線としてのアステロイド アステロイド(英: astroid[1])の語義はギリシア語: aster(星の)+ -oid(ようなもの)であり、星芒形(せいぼうけい)、星形とも呼ばれる。アステロイドは四つの尖点を持つ内サイクロイド(四尖点内擺線)であり、四尖点形 (tetracuspid) の名称も古くから用いられている(ほかには、cubocycloid, paracycle など)。アステロイドを縮閉、伸開、包絡などの概念を用いて他の曲線から得ることができる。類似の曲線として楕円の縮閉線がある。また、アステロイドはスーパー楕円の一種である。
性質
直交座標系において一般に a を任意の実数として

と表される図形をアステロイドと総称する。これらは全て標準アステロイド

に相似である。パラメータ表示では

となる。これは半径 a の円に内接し、かつ x軸、y軸に対して線対称である。曲線で囲まれた面積は  、曲線の弧長は
、曲線の弧長は  である。
である。
半径 a の円内をその1/4の半径を持つ円が滑ることなく転がるとき、内円の円周上の任意の一点の軌跡はアステロイド

を描く。標準アステロイドは、

と書くこともできるが、これは半径比が n + 1 : 1 の内擺線(の n = 3 の場合)としての表示である。
x-軸および y-軸に片方ずつの端点が載っているような長さ一定の線分族は全て一つのアステロイドに接する。したがってそのような線分族の包絡線はアステロイドを描く。
アステロイドの縮閉線はアステロイド(を2倍にして、45度回転させたもの)である。
アステロイドは種数 0 の平面代数曲線の実軌跡として、代数方程式

で表すことができる。これは六次の曲線で実平面 R2 上に(星の頂点の部分に)四つの尖点特異性を持つ。また、複素変数(リーマン球面)に拡張して、さらに二つの尖点特異性を無限遠点にもち、四つの二重点があるから、計10個の特異点をもつことになる。
この式で表されるアステロイドの双対曲線は十字曲線 x2 y2 = x2 + y2 である。
代数方程式の導出

の両辺を3乗すると:



再び両辺を3乗すると:

ここで:

だったので

これより:

よって

一般化
アステロイドはスーパー楕円あるいはラメ曲線と呼ばれる曲線

の α = 2/3, a = b とした特別な場合であり、また a ≠ b を許した

で表される曲線はアステロイドを軸の方向に引き伸ばしあるいは押しつぶした形になる。例えば楕円の縮閉線は(二焦点を原点対称となるように x-軸あるいは y-軸上に配置すれば)この形に表すことができる。これのパラメータ表示は

で示され、曲線で囲まれた面積は

であり、曲線の弧長は

となる。
脚注
- ^ 英語で asteroid と表記されることもあるが、これは小惑星の意味を持つため、区別のためには astroid(アストロイド)が望ましい。日本語表記ではアステロイドがよく用いられる。
参考文献
- Lawrence, J. Dennis (1972), A catalog of special plane curves, Dover Publications, pp. 4–5,34–35,173–174, ISBN 0-486-60288-5
- Wells, D. (1991), The Penguin Dictionary of Curious and Interesting Geometry, New York: Penguin Books, pp. 10–11, ISBN 0-14-011813-6
- Yates, R.C. (1952), “Astroid”, A Handbook on Curves and Their Properties, Ann Arbor, MI: J. W. Edwards, pp. 1 ff.
関連項目
- ストーナー=ウォールファース・アステロイド(磁化反転アステロイド):磁気学で用いられる。
- デルトイド(シュタイナーの内擺線、三尖曲線、オイラーのデルタ)
外部リンク
- 『アステロイド』 - コトバンク
- 『星芒形』 - コトバンク
- 『アステロイド曲線の重要な性質まとめ』 - 高校数学の美しい物語
- Weisstein, Eric W. "Astroid". mathworld.wolfram.com (英語).
- "Astroid" at The MacTutor History of Mathematics archive
- Article on 2dcurves.com
- Visual Dictionary Of Special Plane Curves, Xah Lee
- Bars of an Astroid by Sándor Kabai, The Wolfram Demonstrations Project.






























