 カルノー図の例
カルノー図の例 カルノー図(カルノーず、英: Karnaugh map)は論理回路などにおいて論理式を簡単化するための表であり、その方法をカルノー図法という。よく似た概念にベイチ (Veitch) 図と呼ばれる図があり、変数と数字の書き方のみが異なる。
概要
カルノー図は1950年代にベル研究所のモーリス・カルノー(Maurice Karnaugh)によって発明された。
論理式を簡略化することにより、回路に使う素子を減らすなどのメリットがある。また、ブール代数の公式などを使って論理式を簡略化するよりも比較的楽にできる場合が多い。これはハミング距離が1となるように図が組まれており(図の入力欄の隣同士の真偽値が1つだけ違うように)、感覚的、視覚的な方式で簡略化ができるためである。この入力欄の順序はグレイコードを生成するアルゴリズムで作成できる。
特に

といった論理積の項を論理和した形(積和標準形)の場合に使いやすい。
入力を1次元につき2つまでとすれば立体的にカルノー図を考えることで(人間の次元認識能力の見地から)実質6入力まで対応できる。しかし、実際は平面的に考えることが多く、その場合は縦横各2次元の4入力までである。それ以上の入力にはカルノー図は適していない。ベン図やベイチ図、カルノー図などの図で考える手法では見落とす場合もあるため、クワイン・マクラスキー法などの機械的な方法がより確実である。
図例

3変数のカルノー図例 | A\BC | 00 | 01 | 11 | 10 |
| 0 | | 1 | 1 | |
| 1 | 1 | | | 1 |
3変数のベイチ図例 |  |  |
 | 1 | | 1 | |
 | 1 | | 1 | |
|  |  |  |

4変数のカルノー図例 | AB\CD | 00 | 01 | 11 | 10 |
| 00 | 1 | 1 | 1 | |
| 01 | 1 | 1 | | |
| 11 | | | | |
| 10 | | 1 | 1 | |
4変数のベイチ図例 |  | | |
 | | | | 1 | |
| | | 1 |  |
| | 1 | 1 | 1 | 1 |
| | | 1 | |
| |  | | |

5変数の例 | AB\CDE | 000 | 001 | 011 | 010 | 110 | 111 | 101 | 100 |
| 00 | 1 | 1 | | | | 1 | 1 | 1 |
| 01 | | | 1 | | | 1 | | |
| 11 | | | 1 | | | 1 | | |
| 10 | 1 | 1 | | | | | 1 | 1 |
例
カルノー図で論理式を簡単にする例をしめす。
例1
論理式

をカルノー図で簡単にすることを考える。
カルノー図で、この論理式が真となる部分に「1」を記入すると「図1」のようになる。「図1」で(1)(2)(3)は、それぞれ
 ,
, ,
,
である。
「図1」で論理式が真となる部分(「1」が記入されている部分)を、まとめると「図2」のようになる。「図2」で(1)(2)は、それぞれ
 ,
,
である。
よって、

とわかる。
例2
論理式

をカルノー図で簡単にすることを考える。
カルノー図で、この論理式が真となる部分に「1」を記入すると「図3」のようになる。「図3」で(1)(2)(3)(4)(5)は、それぞれ
 ,
, ,
, ,
, ,
,
である。
「図3」で論理式が真となる部分(「1」が記入されている部分)を、まとめると「図4」のようになる。「図4」で(1)(2)(3)は、それぞれ
 ,
, ,
, ,
,
である。
よって、

とわかる。
関連項目

 図1
図1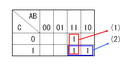 図2
図2 図3
図3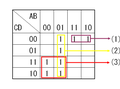 図4
図4







































