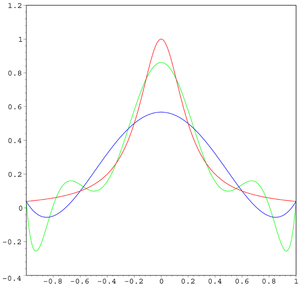
赤はコーシー・ローレンツ関数。青は5次の補間多項式。緑は9次の補間多項式(補間点は等間隔)。 補間点では関数と補間多項式は誤差が(定義上)ゼロである。補間点と補間点の間(特に 1 や −1 に近い部分)では、補間多項式を高次にした方が誤差が大きくなっている。 ルンゲ現象 (ルンゲげんしょう、英語 : Runge's phenomenon )は、数値解析 で高次の多項式で多項式補間 する際に発生する問題である。カール・ルンゲ が、ある関数を多項式補間で近似したときの誤差を調べていて発見した[1]
問題 次の関数(コーシー-ローレンツ関数 )を考える。
f ( x ) = 1 1 + 25 x 2 {\displaystyle f(x)={\frac {1}{1+25x^{2}}}} 次のような −1 から 1 までの等間隔の点 x i 内挿 する。
x i = − 1 + 2 ( i − 1 ) n , i ∈ { 1 , 2 , … , n + 1 } {\displaystyle x_{i}=-1+{\frac {2(i-1)}{n}},\quad i\in \left\{1,2,\dots ,n+1\right\}} このときルンゲは、次数 ≤ n の多項式 P n x ) を用いると、区間の端の方(−1 および 1)に行くに従って補間結果が振動することを発見した。このことは、多項式の次数を大きくしていくと補間誤差が無限大に漸近することで証明できる。
lim n → ∞ ( max − 1 ≤ x ≤ 1 | f ( x ) − P n ( x ) | ) = ∞ {\displaystyle \lim _{n\rightarrow \infty }\left(\max _{-1\leq x\leq 1}|f(x)-P_{n}(x)|\right)=\infty } しかし、ワイエルシュトラスの近似定理 によれば、多項式による近似で誤差がゼロに近づくシーケンスが存在するはずである。このことは、高次多項式補間では等間隔の点から補間することが問題を生じることがあることを示している。
原因 関数とN 次補間多項式の誤差は、関数のN 次導関数に制限される。
上記示した関数の2次までの導関数 は次のようになる。
f ′ ( x ) = − 50 x ( 1 + 25 x 2 ) 2 ⇒ | f ′ ( 1 ) | = 50 26 2 ≈ 0.0740 f ″ ( x ) = 5000 x 2 ( 1 + 25 x 2 ) − 50 ( 1 + 25 x 2 ) 2 ( 1 + 25 x 2 ) 4 ⇒ | f ″ ( 1 ) | = 96200 26 4 ≈ 0.2105 {\displaystyle {\begin{aligned}f'(x)=-{\frac {50x}{\left(1+25x^{2}\right)^{2}}}&\Rightarrow \left|f'(1)\right|={\frac {50}{26^{2}}}\approx 0.0740\\f''(x)={\frac {5000x^{2}(1+25x^{2})-50(1+25x^{2})^{2}}{\left(1+25x^{2}\right)^{4}}}&\Rightarrow \left|f''(1)\right|={\frac {96200}{26^{4}}}\approx 0.2105\end{aligned}}} 見ての通り、高次の導関数の方が大きくなっている。従って、(補間点間の)誤差の上限も補間多項式の次数が高くなるほど大きくなる。
緩和方法 振動を最小化するには、等間隔のノード(補間点)ではなくチェビシェフノード(英語版) を使えばよい。チェビシェフノードは区間の端に集まる傾向がある。この場合、多項式の次数を高くすると誤差が少なくなることを保証できる。一般にルンゲ現象があるため、高次の多項式補間を等間隔ノードで使うのは不適切である。スプライン曲線 による近似を使うという方法もある。その場合、多項式の次数を上げずに、曲線を構成する多項式の断片の数を増やせば誤差を小さくできる。
脚注 [脚注の使い方 ]
^ Runge, Carl (1901年), “Über empirische Funktionen und die Interpolation zwischen äquidistanten Ordinaten”, Zeitschrift für Mathematik und Physik 46 : 224–243 関連項目