Diâmetro angular

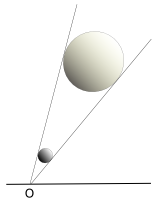
Em astronomia e geometria, o diâmetro angular de um objeto é o diâmetro aparente do objeto a um certa distância medido em graus (º).

Na astronomia o diâmetro angular é usado para medir o tamanho de objetos no céu, como visto da Terra. Conhecendo a distância até o objeto e seu diâmetro angular é possível então calcular o seu tamanho real.

O diâmetro angular da órbita da Terra quando vista de uma distância de 1 parsec é igual a 2″ (2 segundos de arco).

Calculando o diâmetro angular

Suponha um objeto de diâmetro d a uma distância R. O ângulo aparente pelo qual vemos o objeto pode ser obtido pela tangente:

${\displaystyle \tan(\delta )={\frac {d}{R}}}$

portanto

${\displaystyle \delta =\arctan \left({\frac {d}{R}}\right)}$

Nosso problema é então calcular ${\displaystyle \delta }$. Mas a definição acima dará ${\displaystyle \delta }$ em unidades de radianos, para convertermos para arco, ou graus (°), temos que levar em conta que um ângulo de 360° tem ${\displaystyle 2\pi }$ radianos.

Para uso em astronomia, podemos utilizar um simplificação da expressão acima para o diâmetro aparente. Isto porque na grande maioria dos casos os distâncias que estamos observando são muito maiores do que os diâmetros. Neste caso podemos aproximar o diâmetro angular como:

${\displaystyle \delta ={\frac {d}{R}}}$

Convertendo ${\displaystyle \delta }$ para °, usando uma regra de três simples, temos:

${\displaystyle \delta ={\frac {d}{R}}\times {\frac {360}{2\pi }}}$

Em astronomia normalmente podemos medir ${\displaystyle \delta }$ e algumas vezes sabemos o diâmetro ou a distância. A formula acima pode então ser utilizada para calcular uma das grandezas desconhecidas.

Exemplo

Qual a distância que é necessário colocar um moeda para que seu diâmetro angular seja de 1°?.

Suponhamos para simplificar que a moeda tenha 1 cm de diâmetro. Portanto queremos ${\displaystyle \delta =1^{o}}$ para d = 1 cm, temos:

${\displaystyle 1^{o}={\frac {1cm}{R}}\times {\frac {360}{2\pi }}=57,29746\ cm}$

Isto daria uma distância de aproximadamente 57 centímetros. Agora você sabe como enxergar uma ângulo de 1°: um centímetro a distância de um braço estendido tem aproximadamente um diâmetro angular de 1°.

Para entender o que seria um minuto de arco, 1/60 avos de 1°, é só calcular a distância para colocar esta moeda de 1 cm de forma que o diâmetro angular seja 1′ de arco

${\displaystyle 1'=1/60\times 1^{o}={\frac {1cm}{R}}\times {\frac {360}{2\pi }}}$

Ou

${\displaystyle R=60\times {\frac {1cm}{R}}\times {\frac {360}{2\pi }}=3437,847cm=34,37m}$

Continuando este cálculo, podemos mostrar que um segundo de arco (1′ divido por 60) seria então o diâmetro angular de uma moeda de 1 cm a 2,1 Km de distância. A area total da capsula que apresenta 54 cm de diâmetro interno e 4,5 m de altura é de aproximadamente? dado pi=3,14

Ver também

• parsec