Teorema dos círculos inscritos iguais

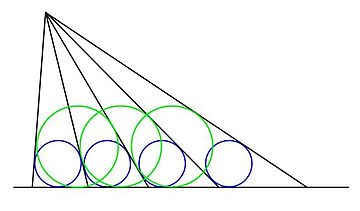
Teorema dos círculos inscritos iguais, em geometria, deriva de um Sangaku japonês, e refere-se a seguinte construção: uma série de raios são desenhados a partir de um determinado ponto de uma determinada linha de tal forma que os círculos inscritos nos triângulos formados por raios adjacentes e a linha de base são iguais. Na ilustração os círculos azuis iguais definem o espaço entre os raios, como descrito.

O teorema afirma que os círculos inscritos dos triângulos formados (a partir de um determinado raio) por todos os outros raios, a cada três raios, etc, e a linha de base também são iguais. O caso de todos os outros raios é ilustrado acima pelos círculos verdes, que são todos iguais.

A partir do fato de que o teorema não depende do ângulo do raio inicial, pode ser visto que o teorema adequadamente pertence à análise, ao invés da geometria, e deve estar relacionado com uma função de escala contínua que define o espaçamento dos raios. Na verdade, esta função é o seno hiperbólico.

O teorema é um corolário direto do seguinte lema:

Suponha que o raio enésima faz um ângulo ${\displaystyle \gamma \,_{n}}$ com a normal à linha de base. Se ${\displaystyle \gamma \,_{n}}$ é parametrizado segundo a equação, ${\displaystyle \tan \gamma \,_{n}=\sinh \theta \,_{n}}$ então valores de ${\displaystyle \theta \,_{n}=a+nb}$, onde ${\displaystyle \!a}$ e ${\displaystyle \!b}$ são constantes reais, define uma sequência de raios que satisfazem a condição de círculos inscritos iguais, e, além disso, qualquer sequência de raios que satisfaçam a condição pode ser produzido pela escolha adequada das constantes ${\displaystyle \!a}$ e ${\displaystyle \!b}$.

Referências

• Equal Incircles Theorem - cut-the-knot
• J. Tabov. A note on the five-circle theorem. Mathematics Magazine 63 (1989), 2, 92–94.