Spirală sinusoidală

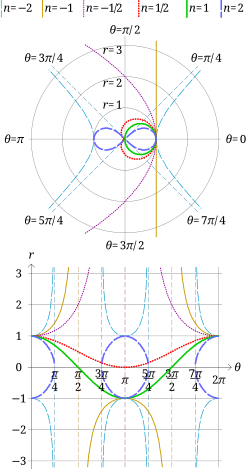
Spirale sinusoidale (rn = –1n cos(nθ), θ = π/2) în coordonate polare și echivalentele lor în coordonate carteziene:                      n = −2: Hiperbolă echilaterală                      n = −1: Dreaptă                      n = −1/2: Parabolă                      n = 1/2: Cardioidă                      n = 1: Cerc                      n = 2: Lemniscata lui Bernoulli

În geometria algebrică spiralele sinusoidale sunt o familie de curbe definite de ecuația în coordonate polare[1]

r n = a n cos ⁡ ( n θ ) {\displaystyle r^{n}=a^{n}\cos(n\theta )}

unde a este o constantă diferită de zero, iar n este un număr rațional altul decât 0. Cu o rotație în jurul originii, aceasta poate fi de asemenea scrise

r n = a n sin ⁡ ( n θ ) . {\displaystyle r^{n}=a^{n}\sin(n\theta ).}

Termenul de „spirală” este o denumire greșită, deoarece de fapt nu sunt spirale⁠(d), ci adesea au o formă asemănătoare unei rozete⁠(d). Multe curbe bine-cunoscute sunt spirale sinusoidale, de exemplu:

  • Hiperbola echilaterală (n = −2)
  • Dreapta (n = −1)
  • Parabola (n = −1/2)
  • Cubica Tschirnhausen (n = −1/3)
  • Sextica lui Cayley (n = 1/3)
  • Cardioida (n = 1/2)
  • Cercul (n = 1)
  • Lemniscata lui Bernoulli (n = 2)

Această familie de curbe a fost studiată pentru prima oară de Colin Maclaurin.

Ecuații

Prin derivarea lui

r n = a n cos ⁡ ( n θ ) {\displaystyle r^{n}=a^{n}\cos(n\theta )}

și eliminarea lui a se obține ecuația diferențială în r și θ:

d r d θ cos ⁡ n θ + r sin ⁡ n θ = 0 {\displaystyle {\frac {dr}{d\theta }}\cos n\theta +r\sin n\theta =0} .

Atunci

( d r d s ,   r d θ d s ) cos ⁡ n θ d s d θ = ( − r sin ⁡ n θ ,   r cos ⁡ n θ ) = r ( − sin ⁡ n θ ,   cos ⁡ n θ ) {\displaystyle \left({\frac {dr}{ds}},\ r{\frac {d\theta }{ds}}\right)\cos n\theta {\frac {ds}{d\theta }}=\left(-r\sin n\theta ,\ r\cos n\theta \right)=r\left(-\sin n\theta ,\ \cos n\theta \right)}

care implică faptul că unghiul tangențial polar este

ψ = n θ ± π / 2 {\displaystyle \psi =n\theta \pm \pi /2}

și deci unghiul tangențial este

φ = ( n + 1 ) θ ± π / 2 {\displaystyle \varphi =(n+1)\theta \pm \pi /2} .

(Semnul de aici este pozitiv dacă r și cos nθ au același semn și negativ în caz contrar.)

Comparând versorul tangent

( d r d s ,   r d θ d s ) {\displaystyle \left({\frac {dr}{ds}},\ r{\frac {d\theta }{ds}}\right)} ,

cu mărimea vectorilor de pe fiecare parte a ecuației de mai sus se obține

d s d θ = r cos − 1 ⁡ n θ = a cos − 1 + 1 n ⁡ n θ {\displaystyle {\frac {ds}{d\theta }}=r\cos ^{-1}n\theta =a\cos ^{-1+{\tfrac {1}{n}}}n\theta } .

În particular, lungimea unei singure bucle când n > 0 {\displaystyle n>0} este:

a ∫ − π 2 n π 2 n cos − 1 + 1 n ⁡ n θ   d θ {\displaystyle a\int _{-{\tfrac {\pi }{2n}}}^{\tfrac {\pi }{2n}}\cos ^{-1+{\tfrac {1}{n}}}n\theta \ d\theta }

Curbura este

d φ d s = ( n + 1 ) d θ d s = n + 1 a cos 1 − 1 n ⁡ n θ {\displaystyle {\frac {d\varphi }{ds}}=(n+1){\frac {d\theta }{ds}}={\frac {n+1}{a}}\cos ^{1-{\tfrac {1}{n}}}n\theta } .

Proprietăți

Inversa unei spirale sinusoidale în raport cu un cerc cu centrul în origine este o altă spirală sinusoidală a cărei valoare a lui n este negativul valorii curbei originale a lui n. De exemplu, inversa lemniscatei lui Bernoulli este o hiperbolă dreptunghiulară.

Isoptica⁠(d), podara și podara negativă ale unei spirale sinusoidale sunt spirale sinusoidale diferite.

Traiectoria unei particule asupra căreia acționează o forță centrală proporțională cu o putere a lui r este o spirală sinusoidală.

Când n este un număr întreg și punctele n sunt aranjate regulat pe un cerc cu raza a, atunci mulțimea punctelor aranjate astfel încât media geometrică a distanțelor de la punct la n formează o spirală sinusoidală. În acest caz, spirala sinusoidală este o lemniscată polinomială.

Note

  1. ^ Dănuț Zahariea, Limbaje de programare structurata: Aplicații MATLAB, tuiasi.ro, 2017, p. 194, accesat 2023-05-20

Bibliografie

  • en Yates, R. C.: A Handbook on Curves and Their Properties, J. W. Edwards (1952), "Spiral" p. 213–214
  • en "Sinusoidal spiral" at www.2dcurves.com
  • en "Sinusoidal Spirals" at The MacTutor History of Mathematics
  • en Eric W. Weisstein, Sinusoidal Spiral la MathWorld.

Legături externe

Portal icon Portal Matematică