Tetraedar

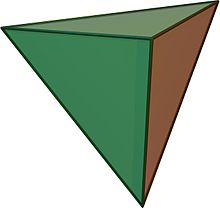
Tetraedar (grč. tetráedron) je geometrijsko telo koga ograničavaju četiri temena površi, koje zajedno sa delom prostora koga omeđuju jednoznačno formiraju telo sa četiri temena i šest ivica. Naziv se u principu koristi za pravilni tetraedar, kod koga su ove četiri površi identični jednakostranični trouglovi. Pravilni tetraedar je jedan od pet pravilnih poliedara.

Svojstva pravilnog tetraedra

Neke od osnovnih karakteristika tetraedra su određene sledećim formulama:

Površina	${\displaystyle P={\sqrt {3}}a^{2}}$
Zapremina	${\displaystyle V={\begin{matrix}{1 \over 12}\end{matrix}}{\sqrt {2}}a^{3}}$
Poluprečnik opisane sfere	${\displaystyle r_{o}\,=\,{\frac {\sqrt {6}}{4}}\,a\approx 0{,}61\,a}$
Poluprečnik upisane sfere	${\displaystyle r_{u}\,=\,{\frac {\sqrt {6}}{12}}\,a\approx 0{,}20\,a}$
Visina	${\displaystyle h=r_{o}+r_{u}\,=\,{\frac {\sqrt {6}}{3}}\,a\,=\,{\sqrt {\frac {2}{3}}}\,a\approx 0{,}82\,a}$
Ugao između ivice i površi	${\displaystyle arctg{\sqrt {2}}\approx 55^{\circ }}$
Ugao između dve površi	${\displaystyle \arccos {1/3}=arctg2{\sqrt {2}}\approx 71^{\circ }}$

Pregled

Tetraedar je trodimenzijski slučaj općeg koncepta euklidskog simpleksa. To je jedan od oblika piramida, koji je poliedar s ravnom poligonskom bazom i trokutastoim licem koje povezuje bazu za zajedničkom tjemenom tačkom. U slučaju kada je tetraedarska baza trougao (bilo koje od četiri lica može se smatrati bazom), takav tetraedar je također poznat kao "trouglasta piramida

Kao i svi konveksni poliedri, tetraedar može biti sastavljen iz jednog lista papira. On ima takvu mrežu.

Milo koji tetraedar ima sferu (zvanu cirkumsfera) na kojoj leže sva četiri i drugu sferu (insfera), koja je tangenta površina tetraedra.

Pravilni tetraedar

Pravilni tetraedar je onaj u kojem su sva četiri lica su istostrani trouglovi. To je jedan od pet pravilnih platonskih čvrstih tvari, koje su poznate od davnina.

Kod pravilnog tetraedra, ne samo da su sve njegove strane iste veličine i oblika (podudarne), nego su takvi i sve njegovi vrhova i rubovi.

Pravilni tetraedra nije samo popunjen prostor, nego ako je naizmeničan sa pravilnim oktaedrom, oni čine naizmenično kubno saće, koji je prazan.

Tetraedar je samo-dualan, što znači da je njegov dvojnik drugi tetraedar. Spoj slika sastoji se od dva takva dualna tetraedra koji formiraju zvjezdasti oktaedar ili zvjezdasti oktaugao.

Tretraedarske formula

Slijedeće Dekartove koordinate definiraju četiri tjemena tetraedra dužine ruba 2, centrirana prema porijeklu:

${\displaystyle \left(\pm 1,0,-{\frac {1}{\sqrt {2}}}\right)\quad {\mbox{and}}\quad \left(0,\pm 1,{\frac {1}{\sqrt {2}}}\right)}$

Drugi set koordinata se zasniva na naizmeničnoj kocki ili demikubu dužine ruba 2. Ovaj oblik ima Coxeterov dijagram 4x3 i Schläfli simbol h {4,3}. Tetraedar u ovom slučaju ima dužinu ruba 2. Invertiranje ove koordinate generira dualni tetraedar i taj par zajedno formira zvjezdasti oktaedar, čija tjemena su one originalne kocke .

Tetraedar: (1,1,1), (1,−1,−1), (−1,1,−1), (−1,−1,1)

Dualni tetraedar: (−1,−1,−1), (−1,1,1), (1,−1,1), (1,1,−1)

Za tetraedra dužine ruba a:

Površina lica	${\displaystyle A_{0}={\frac {\sqrt {3}}{4}}a^{2}\,}$
Površinsko područje[1]	${\displaystyle A=4\,A_{0}={\sqrt {3}}a^{2}\,}$
Visina piramide[2]	${\displaystyle h={\frac {\sqrt {6}}{3}}a={\sqrt {\frac {2}{3}}}\,a\,}$
Rubovi suprotne rubne distance	${\displaystyle l={\frac {1}{\sqrt {2}}}\,a\,}$
aVolumen[1]	${\displaystyle V={\frac {1}{3}}A_{0}h={\frac {\sqrt {2}}{12}}a^{3}={\frac {a^{3}}{6{\sqrt {2}}}}\,}$
Ugao lice-tjeme-rub	${\displaystyle \arccos \left({\frac {1}{\sqrt {3}}}\right)=\arctan \left({\sqrt {2}}\right)\,}$ (približno 54,7356°)
Ugao lice-rub-lice, tj. "diedarski ugao"[1]	${\displaystyle \arccos \left({\frac {1}{3}}\right)=\arctan \left(2{\sqrt {2}}\right)\,}$ (približno 70,5288°
Centralni rubni ugao,[3][4] poznat kao tetraedarski ugao	${\displaystyle \arccos \left(-{\frac {1}{3}}\right)=2\arctan \left({\sqrt {2}}\right)\,}$ (approx. 109.4712°)
Čvrsti ugao na tjemenu naspram lica	${\displaystyle \arccos \left({\frac {23}{27}}\right)}$ (približno 0,55129 steradijana)
Radijus cirkumsfere[1]	${\displaystyle R={\frac {\sqrt {6}}{4}}a={\sqrt {\frac {3}{8}}}\,a\,}$
Radijus insfere koji je tangenta lica[1]	${\displaystyle r={\frac {1}{3}}R={\frac {a}{\sqrt {24}}}\,}$
Radijus srednje sfere koja je tangenta rubovima[1]	${\displaystyle r_{\mathrm {M} }={\sqrt {rR}}={\frac {a}{\sqrt {8}}}\,}$
Radijus eksfera	${\displaystyle r_{\mathrm {E} }={\frac {a}{\sqrt {6}}}\,}$
Distanca od centra eksfere do suprotnog tjemena	${\displaystyle d_{\mathrm {VE} }={\frac {\sqrt {6}}{2}}a={\sqrt {\frac {3}{2}}}a\,}$

U odnosu na baznu ravni nagib lica (2Šablon:Sqrt) je dva puta veći od ivice (Šablon:Sqrt), što odgovara činjenici da je horizontalna udaljenost od baze do apeksa duž ivice dva puta veća od medijane lica. Drugim riječima, ako je C težište baze, udaljenost od C do tjemena baze je dvostruko veća od centralne tačke C do ruba baze. To proizlazi iz činjenice da je medijane trougla sijeku svojim težištem i tada dijele svaku od njih u dva segmenta, od kojih je jedan duplo veći, dok drugi dijeli svaku medijanu u omjeru 2 : 1.

Za pravilni tetraedar sa stranom dužine a, radijusom R njegove cirkumsfere i udaljenosti d_i iz proizvoljne tačke u 3-dimenzijskom prostoru za njegova četiri tjemena, imamo:^[5]

${\displaystyle {\begin{aligned}{\frac {d_{1}^{4}+d_{2}^{4}+d_{3}^{4}+d_{4}^{4}}{4}}+{\frac {16R^{4}}{9}}&=\left({\frac {d_{1}^{2}+d_{2}^{2}+d_{3}^{2}+d_{4}^{2}}{4}}+{\frac {2R^{2}}{3}}\right)^{2};\\4\left(a^{4}+d_{1}^{4}+d_{2}^{4}+d_{3}^{4}+d_{4}^{4}\right)&=\left(a^{2}+d_{1}^{2}+d_{2}^{2}+d_{3}^{2}+d_{4}^{2}\right)^{2}.\end{aligned}}}$

Povezano

• Poliedar
• Kocka

Reference

Pri tom je a dužina ivice tetraedra.

Tetraedar na Wikimedijinoj ostavi