Poenkareova hipoteza

U matematici, Poenkareova hipoteza je teorema o karakterizaciji 3-sfere, koja je hipersfera koja ograničava jediničnu loptu u četvorodimenzionalnom prostoru.^[1][2][3]

Ova hipoteza navodi:

Svaka jednostavno povezana, zatvorena 3-mnogostrukost je homeomorfna sa 3-sferom.

Ekvivalentni oblik hipoteze predstavlja grublja forma ekvivalencije od homeomorfizma koja se naziva homotopska ekvivalencija: ako je 3-mnogostrukost homotopno ekvivalentna 3-sferi, onda je to nužno homeomorfna na njoj.

Ova hipoteza koju je prvobitno postavio Anri Poenkare, odnosi se na prostor koji lokalno izgleda kao obični trodimenzionalni prostor, ali je povezan, konačne veličine i nema bilo kakve granice (zatvorena 3-mnogostrukost). Poenkareova pretpostavka tvrdi da ako takav prostor ima dodatno svojstvo da se svaka petlja u prostoru može neprekidno stezati do tačke, on je nužno trodimenzionalna sfera. Analogne pretpostavke za sve više dimenzije već su bile dokazane.

Nakon što su skoro ceo jedan vek matematičari nastojali da dokažu ovu hipotezu, Grigorij Pereljman je predstavio dokaz pretpostavke u tri rada, koja su objavljena 2002. i 2003. godine na arXiv. Dokaz je baziran na programu Ričarda S. Hamiltona da koristi Ričijev tok za pokušaj rešavanja problema. Kasnije je Hamilton uveo modifikaciju standardnog Ričijevog toka, zvanu Ričijev tok hirurškim zahvatom da sistematski izrezuje pojedinačne regije kako se razvijaju, na kontrolisan način, ali nije uspeo da dokaže da ova metoda „konvergira” u tri dimenzije.^[4] Perelman je kompletirao ovaj deo dokaza. Nekoliko timova matematičara potvrdilo je da je Perelmanov dokaz tačan.

Poenkareova hipoteza, pre nego što je dokazana, bila je jedno od najvažnijih otvorenih pitanja u topologiji. Godine 2000, proglašena je jednim od sedam Milenijumskih nagradnih problema za koji je Klejov institut za matematiku ponudio nagradu od milion dolara za prvo ispravno rešenje. Perelmanov rad je preživeo pregled i potvrđen je 2006. godine, što je dovelo do toga da mu je ponuđena Fildsova medalja, koju je on odbio. Perelman je nagrađen Milenijumskom nagradom 18. marta 2010. godine.^[5] Dana 1. jula 2010. godine on je odbio nagradu rekavši da veruje da njegov doprinos u dokazivanju Poenkareove hipoteze nije veći od Hamiltonovog.^[6][7] Prema podacima iz 2020. godine, Poenkareova hipoteza je jedini rešeni Milenijumski problem.

Dana 22. decembra 2006. godine časopis Science odao je počast Perelmanovom dokazu Poenkareove hipoteze kao „Proboju godine”, prvi put kada je ta počast dodeljena u oblasti matematike.^[8]

Istorija

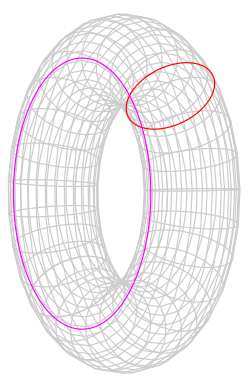
Poenkareovo pitanje

Anri Poenkare je radio na osnovama topologije — što je kasnije postalo poznato kao kombinatorna topologija, a zatim algebarska topologija. Posebno ga je zanimalo koja topološka svojstva karakterišu sferu.

Poenkare je 1900. godine tvrdio da je homologija, alat koji je osmislio na osnovu prethodnog rada Enrika Betija, dovoljna da se kaže da li je 3-mnogostruka 3-sfera. Međutim, u radu iz 1904. opisao je kontraprimer za ovu tvrdnju, prostor koji se sada zove Poenkareova homološka sfera. Poenkareova sfera je bila prvi primer homološke sfere, mnogostrukosti koja je imala istu homologiju kao sfera, od koje su od tada konstruisane mnoge druge. Da bi utvrdio da je Poenkareova sfera drugačija od 3-sfere, Poenkare je uveo novu topološku invarijantu, fundamentalnu grupu, i pokazao da Poenkareova sfera ima fundamentalnu grupu reda 120, dok je 3-sfera imala trivijalnu fundamentalnu grupu. Na taj način je mogao da zaključi da su ova dva prostora, zaista, različita.

U istom radu, Poenkare se zapitao da li 3-mnogostrukost sa homologijom 3-sfere i takođe trivijalne fundamentalne grupe mora biti 3-sfera. Poenkareov novi uslov — to jest, „trivijalna fundamentalna grupa“ — može se ponovo izreći kao „svaka petlja se može smanjiti do tačke“.

Originalna fraza je bila sledeća:

Razmotrimo kompaktnu 3-dimenzionalnu mnogostrukost V bez granice. Da li je moguće da bi osnovna grupa V mogla biti trivijalna, iako V nije homeomorfna trodimenzionalnoj sferi?

Poenkare nikada nije izjavio da li veruje da će ovaj dodatni uslov karakterisati 3-sferu, ali bez obzira na to, izjava koja to čini je poznata kao Poenkareova pretpostavka. Ovo je standardni oblik pretpostavke:

Svaka jednostavno povezana, zatvorena 3-mnogostrukost je homeomorfna 3-sferi.

Treba imati na umu da „zatvoreno” ovde znači, kao što je uobičajeno u ovoj oblasti, uslov da je kompaktno u smislu topologije skupa, a takođe i bez granica (3-dimenzionalni euklidski prostor je primer jednostavno povezane 3-mnogostrukosti koja nije homeomorfna sa 3-sferom; ali nije kompaktna i stoga nije kontra-primer).

Rešenja

Tokom 1930-ih, Dž. H. K. Vajthed je tvrdio da ima dokaz, ali ga je potom povukao. U tom procesu, otkrio je neke primere jednostavno povezanih (zaista kontraktivnih, tj. homotopski ekvivalentnih tački) nekompaktnih 3-mnogostrukosti koje nisu homeomorfne sa ${\displaystyle \mathbb {R} ^{3}}$, prototipom koji se sada zove Vajthedova mnogostrukost.

Tokom 1950-ih i 1960-ih, drugi matematičari su pokušavali da dokažu pretpostavku samo da bi otkrili da njihova rešenja sadrže nedostatke. Uticajni matematičari kao što su Žorž de Ram, R. H. Bing, Volfgang Haken, Edvin E. Mojz i Hristos Papakirijakopulos pokušali su da dokažu pretpostavku. Godine 1958, R. H. Bing je dokazao slabu verziju Poenkareove pretpostavke: ako je svaka jednostavna zatvorena kriva kompaktne 3-mnogostrukosti sadržana u 3-lopti, onda je mnogostrukost homeomorfna 3-sferi.^[9] Bing je takođe opisao neke od zamki u pokušaju da dokaže Poenkareovu pretpostavku.^[10]

Vlođimierz Jakobsce je 1978. godine pokazao da, ako je Bing–Borsukova pretpostavka tačna u dimenziji 3, onda i Poenkareova pretpostavka mora biti tačna.^[11]

Vremenom je ova pretpostavka stekla reputaciju posebno teškog problema za rešavanje. Džon Milnor je prokomentarisao da ponekad greške u lažnim dokazima mogu biti „prilično suptilne i teško ih je otkriti.“^[12] Rad na pretpostavci je poboljšao razumevanje 3-mnogostrukosti. Stručnjaci u ovoj oblasti često nisu bili voljni da objave dokaze i bili su skloni da na svaku takvu najavu gledaju sa skepticizmom. Tokom 1980-ih i 1990-ih objavljeno je nekih dobro promovisanioh lažnih dokaza (koji zapravo nisu objavljeni u recenziranom obliku).^[13][14]

Izlaganje pokušaja da se dokaže ova pretpostavka može se naći u netehničkoj knjizi Poenkareova nagrada autora Džordža Špire.^[15]

Reference

Literatura

Spoljašnje veze