Kvantharmonisk oscillator

En kvantharmonisk oscillator är den kvantmekaniska motsvarigheten till den klassiska fysikens harmoniska oscillator. Det är ett system vars återdrivande kraft är proportionell mot avvikelsen från jämviktsläget. Det proportionella förhållandet mellan den återdrivande kraften och avvikelsen från jämviktsläget leder till en kvadratisk potential för systemet. Eftersom en godtycklig potential kan approximeras med en kvadratisk potential kring ett stabilt jämviktsläge är den harmoniska oscillatorn en av de viktigaste modellerna inom kvantmekaniken. Det är dessutom en av få modeller som har en exakt analytisk lösning.

Endimensionell oscillator

Hamiltonoperator

Hamiltonoperatorn ${\displaystyle {\hat {H}}}$ för en partikel i en endimensionell potential ${\displaystyle V(x)}$ ges av

${\displaystyle {\hat {H}}={\frac {{\hat {p}}^{2}}{2m}}+V(x)}$

där ${\displaystyle m}$ är partikelns massa och ${\displaystyle {\hat {p}}=-i\hbar {\frac {\partial }{\partial x}}}$ är rörelsemängdsoperatorn. För en harmonisk oscillator med vinkelfrekvensen ${\displaystyle \omega }$ gäller att potentialen ges av ${\displaystyle V(x)={\frac {1}{2}}m\omega ^{2}x^{2}}$, vilket tillsammans med det allmänna uttrycket för Hamiltonoperatorn ger

Hamiltonoperatorn för endimensionell harmonisk oscillator ${\displaystyle {\hat {H}}={\frac {{\hat {p}}^{2}}{2m}}+{\frac {1}{2}}m\omega ^{2}x^{2}}$

Den första termen i Hamiltonoperatorn motsvarar partikelns kinetiska energi medan den andra termen motsvarar den potentiella energin, som för den harmoniska oscillatorn är kvadratiskt beroende av positionen. Uttrycket för energin är precis samma som för den klassiska harmoniska oscillatorn, men till skillnad från det klassiska fallet så kommuterar inte operatorerna ${\displaystyle {\hat {x}}}$ och ${\displaystyle {\hat {p}}}$ i kvantmekaniken. Istället uppfyller de den kanoniska kommutatorrelationen

Kanoniska kommutatorrelationen för ${\displaystyle {\hat {x}}}$ och ${\displaystyle {\hat {p}}}$ ${\displaystyle [{\hat {x}},{\hat {p}}]=i\hbar }$

Schrödingerekvationen och tidsutveckling

Tidsutvecklingen av ett kvantsystems tillstånd ${\displaystyle |\psi (t)\rangle }$ erhålls från Schrödingerekvationen:

${\displaystyle i\hbar {\frac {\partial }{\partial t}}|\psi (t)\rangle ={\hat {H}}|\psi (t)\rangle }$

En särskild typ av lösning ges på formen ${\displaystyle |\psi (t)\rangle =e^{-iEt/\hbar }|\psi (0)\rangle }$. Ett sådant tillstånd har en väldefinierad energi ${\displaystyle E}$ och kallas för ett egentillstånd till Hamiltonoperatorn eftersom Schrödingerekvationen reduceras till egenekvationen

${\displaystyle {\hat {H}}|\psi (0)\rangle =E|\psi (0)\rangle }$.

Lösningarna till denna tidsoberoende Schrödingerekvation ger de möjliga egentillstånden och egenenergierna. Varje annat tillstånd kan beskrivas som en superposition av egentillstånd eftersom egentillstånden spänner upp hela rummet av möjliga tillstånd.

Ofta projiceras kvanttillstånden på egentillstånden ${\displaystyle |x\rangle }$ till positionsoperatorn ${\displaystyle {\hat {x}}}$. Detta ger partikelns vågfunktion

${\displaystyle \psi (x,t)=\langle x|\psi (t)\rangle =e^{-iEt/\hbar }\langle x|\psi (0)\rangle \equiv e^{-iEt/\hbar }\psi (x)}$.

Vågfunktionen beskriver partikelns rörelse, till exempel ges sannolikhetstätheten för att partikeln befinner sig vid position ${\displaystyle x}$ av ${\displaystyle |\psi (x)|^{2}}$.

Egentillstånd och egenenergier

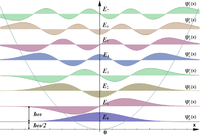Icke-normaliserade vågfunktioner (vänster) med tillhörande sannolikhetstätheter (höger) för de åtta lägsta egentillstånden.

Genom att lösa den tidsoberoende Schrödingerekvationen med någon lämplig metod, till exempel en spektralmetod, kan egentillstånden och egenenergierna för den harmoniska oscillatorn erhållas. Egentillstånden ges av

Egentillstånden för harmoniska oscillatorn ${\displaystyle \psi _{n}(x)={\frac {1}{\sqrt {2^{n}n!}}}\cdot \left({\frac {m\omega }{\pi \hbar }}\right)^{1/4}\cdot e^{-{\frac {m\omega x^{2}}{2\hbar }}}\cdot H_{n}\left({\sqrt {\frac {m\omega }{\hbar }}}x\right)}$

där ${\displaystyle H_{n}(x)}$ betecknar de olika Hermitepolynomen som ges av

${\displaystyle H_{n}(x)=(-1)^{n}e^{x^{2}}{\frac {d^{n}}{dx^{n}}}\left(e^{-x^{2}}\right)}$.

De tillhörande egenenergierna ges av

Egenenergierna för harmoniska oscillatorn ${\displaystyle E_{n}=\hbar \omega \left(n+{\frac {1}{2}}\right)}$

Detta energispektrum är intressant av tre anledningar. För det första är energierna kvantiserade, vilket innebär att bara vissa diskreta energivärden är möjliga. Detta är ett allmänt fenomen hos kvantmekaniska system med instängda partiklar.

För det andra är avståndet mellan två energinivåer konstant, vilket är en viktig skillnad från till exempel Bohrs atommodell eller en partikel i låda.

För det tredje är den lägsta möjliga energin (energin som ges av ${\displaystyle n=0}$, även kallat grundtillståndet) inte lika med potentialens minimum, utan ${\displaystyle \hbar \omega /2}$ ovan minimumet; detta kallas för nollpunktsenergi. På grund av nollpunktsenergin är positionen och rörelsemängden för oscillatorn i grundtillståndet inte fixerats så som är fallet för den klassiska oscillatorn. Detta är en följd av Heisenbergs osäkerhetsrelation som gäller för alla observabler som inte kommuterar. Nollpunktsenergin har betydande konsekvenser för kvantfältteori och kvantgravitation.

Notera att grundtillståndets sannolikhetstäthet är koncentrerad till ${\displaystyle x=0}$. Detta betyder att partikeln tillbringar största delen av sin tid i botten av potentialbrunnen, vilket förväntas av ett tillstånd med låg energi. När energin ökar kommer sannolikhetstätheten att koncentreras till de klassiska ”vändpunkterna”, där den potentiella energin är samma som tillståndets energi. Detta är konsistent med den klassiska harmoniska oscillatorn där partikeln tillbringar mest tid vid vändpunkterna. Korrespondensprincipen är därmed uppfylld. Så kallade koherenta tillstånd oscillerar på ett liknande sätt som klassiska objekt, så som illustrerat i figuren; de är inte egentillstånd till Hamiltonoperatorn.

Stegoperatorer

Metoden med stegoperatorer är ett enkelt sätt att erhålla egentillstånden och egenenergierna för den harmoniska oscillatorn. Metoden kan dessutom generaliseras till mer komplicerad problem inom kvantfältteori. Metoden bygger på användandet av stegoperatorer som definieras genom

Stegoperatorer ${\displaystyle a\equiv {\sqrt {\frac {m\omega }{2\hbar }}}\left({\hat {x}}+{\frac {i}{m\omega }}{\hat {p}}\right)}$ ${\displaystyle a^{\dagger }\equiv {\sqrt {\frac {m\omega }{2\hbar }}}\left({\hat {x}}-{\frac {i}{m\omega }}{\hat {p}}\right)}$

Omvänt kan operatorerna ${\displaystyle {\hat {x}}}$ och ${\displaystyle {\hat {p}}}$ uttryckas i termer av stegoperatorerna ${\displaystyle a}$ och ${\displaystyle a^{\dagger }}$ som

${\displaystyle {\hat {x}}={\sqrt {\frac {\hbar }{2m\omega }}}\left(a^{\dagger }+a\right)}$

${\displaystyle {\hat {p}}=i{\sqrt {\frac {m\omega \hbar }{2}}}\left(a^{\dagger }-a\right)}$

Det följer direkt av definitionen av ${\displaystyle a}$ och ${\displaystyle a^{\dagger }}$ och den kanoniska kommutatorrelationen att

Kanoniska kommutatorrelationen för ${\displaystyle a}$ och ${\displaystyle a^{\dagger }}$ ${\displaystyle [a,a^{\dagger }]=1}$

Således kan Hamiltonoperatorn för den harmoniska oscillatorn skrivas om som

${\displaystyle {\hat {H}}=\left(a^{\dagger }a+{\frac {1}{2}}\right)\equiv \left(N+{\frac {1}{2}}\right)}$

där nummeroperatorn ${\displaystyle N\equiv a^{\dagger }a}$ har införts.

Om ${\displaystyle |n\rangle }$ betecknar ett egentillstånd till ${\displaystyle {\hat {H}}}$ med egenvärdet ${\displaystyle E_{n}=\hbar \omega (n+{\frac {1}{2}})}$ så gäller att

${\displaystyle N|n\rangle =n|n\rangle }$

${\displaystyle Na|n\rangle =(n-1)a|n\rangle }$

${\displaystyle Na^{\dagger }|n\rangle =(n+1)a^{\dagger }|n\rangle }$

vilket innebär att ${\displaystyle N}$ räknar antalet kvanta, ${\displaystyle a}$ minskar antalet kvanta med ett och ${\displaystyle a^{\dagger }}$ ökar antalet kvanta med ett.

Givet ett egentillstånd ${\displaystyle |n\rangle }$ kan nya egentillstånd med lägre antal kvanta erhållas genom att applicera ${\displaystyle a}$ upprepade gånger. Till slut är antalet kvanta lika med noll, vilket motsvarar egentillståndet med egenenergi ${\displaystyle E_{n}=\hbar \omega /2}$. Detta är grundtillståndet och brukar betecknas med ${\displaystyle |0\rangle }$. Om ${\displaystyle a}$ appliceras ytterligare gånger kommer inget nytt tillstånd att erhållas, det vill säga ${\displaystyle a|0\rangle =0}$.

Alla egentillstånd kan uttryckas i termer av grundtillståndet och ${\displaystyle a^{\dagger }}$:

${\displaystyle |n\rangle ={\frac {(a^{\dagger })^{n}}{\sqrt {n!}}}|0\rangle }$

Vågfunktionerna erhålls genom att projicera tillstånden på ${\displaystyle |x\rangle }$. För grundtillståndet gäller till exempel

${\displaystyle \langle x|a|0\rangle =0\Rightarrow \left(x+{\frac {\hbar }{m\omega }}{\frac {d}{dx}}\right)\langle x|0\rangle =0\Rightarrow \langle x|0\rangle =\left({\frac {m\omega }{\pi \hbar }}\right)^{1/4}\exp \left(-{\frac {m\omega }{2\hbar }}x^{2}\right)=\psi _{0}}$

Naturliga längd- och energiskalor

Beskrivningen av kvantharmoniska oscillatorn förenklas om längd- och energiskalorna görs dimensionslösa genom att normaliseras med lämpliga enheter. Om energin mäts i enheter av ${\displaystyle \hbar \omega }$ och avstånd i enheten ${\displaystyle {\sqrt {\hbar /(m\omega )}}}$ så blir Hamiltonoperatorn

${\displaystyle {\hat {H}}=-{\frac {1}{2}}{\frac {d^{2}}{dx^{2}}}+{\frac {1}{2}}x^{2}}$

samtidigt som egenfunktionerna och egenenergierna ges av

${\displaystyle \psi _{n}=\langle x|n\rangle ={\frac {1}{\sqrt {2^{n}n!}}}\pi ^{-1/4}\exp \left(-x^{2}/2\right)H_{n}(x)}$

${\displaystyle E_{n}=n+{\frac {1}{2}}}$

där ${\displaystyle H_{n}(x)}$ betecknar Hermitepolynomen. I vissa fall är dessa naturliga längd- och energiskalor fördelaktiga eftersom det förenklar uttrycken. I andra sammanhang kan det vara fördelaktigt att skriva ut beroendet av ${\displaystyle \omega ,m,\hbar }$ explicit.

Fasrumslösningar

I fasrumsformuleringen av kvantmekaniken kan lösningarna till den kvantharmoniska oscillatorn ges på sluten form i flera olika representationer av kvasisannolikhetsfördelningen. Den mest använda är Wigners kvasisannolikhetsfördelning är

${\displaystyle F_{n}(x)={\frac {(-1)^{n}}{\pi \hbar }}L_{n}\left(4{\frac {u}{\hbar \omega }}\right)\exp \left(-2u/\hbar \omega \right)}$

där

${\displaystyle u={\frac {1}{2}}m\omega ^{2}x^{2}+{\frac {p^{2}}{2m}}}$

och ${\displaystyle L_{n}(x)}$ betecknar Laguerrepolynomen. Detta exempel visar hur Hermitepolynomen och Laguerrepolynomen är relaterade till varandra genom Wigner–Weyltransformen.

N-dimensionell oscillator

Den ${\displaystyle N}$-dimensionella oscillatorn är en generalisering av den endimensionella. Istället för att beskriva partikelns läge med en enda koordinat ${\displaystyle x}$ beskrivs den nu av ${\displaystyle N}$ olika koordinater ${\displaystyle x_{1},x_{2},...,x_{N}}$. De kanoniska kommutatorrelationerna är

${\displaystyle [x_{i},p_{j}]=i\hbar \delta _{ij}}$

${\displaystyle [x_{i},x_{j}]=0}$

${\displaystyle [p_{i},p_{j}]=0}$

Hamiltonoperatorn ges då av

Hamiltonoperatorn för ${\displaystyle N}$-dimensionell harmonisk oscillator ${\displaystyle {\hat {H}}=\sum \limits _{i=1}^{N}{\frac {{\hat {p_{i}}}^{2}}{2m}}+{\frac {1}{2}}m\omega ^{2}x_{i}^{2}}$

Formen på Hamiltonoperatorn avslöjar att den ${\displaystyle N}$-dimensionella harmoniska oscillatorn är exakt samma sak som ${\displaystyle N}$ stycken oberoende harmoniska oscillatorer med samma massa ${\displaystyle m}$ och vinkelfrekvens ${\displaystyle \omega }$. Koordinaterna ${\displaystyle x_{1},x_{2},...,x_{N}}$ kan ses som beskrivningar av ${\displaystyle N}$ olika partiklar.

Lösningen till den ${\displaystyle N}$-dimensionella kvantharmoniska oscillatorn kan erhållas direkt från lösningen till den endimensionella oscillatorn. Vågfunktionen ges av

${\displaystyle \langle \mathbf {x} |\psi _{\{n\}}\rangle =\prod \limits _{i=1}^{N}\langle x_{i}|\psi _{n_{i}}\rangle }$

Analog med endimensionella fallet definieras stegoperatorerna av

Stegoperatorer ${\displaystyle a_{i}\equiv {\sqrt {\frac {m\omega }{2\hbar }}}\left({\hat {x}}_{i}+{\frac {i}{m\omega }}{\hat {p}}_{i}\right)}$ ${\displaystyle a_{i}^{\dagger }\equiv {\sqrt {\frac {m\omega }{2\hbar }}}\left({\hat {x}}_{i}-{\frac {i}{m\omega }}{\hat {p}}_{i}\right)}$

Hamiltonoperatorn ges av

${\displaystyle H=\hbar \omega \sum _{i=1}^{N}\left(a_{i}^{\dagger }a_{i}+{\frac {1}{2}}\right)}$

Energinivåerna för systemet blir

${\displaystyle E=\hbar \omega \left[\left(n_{1}+n_{2}+...+n_{N}\right)+{\frac {N}{2}}\right]}$

där ${\displaystyle n_{i}}$ betecknar antalet kvanta i den ${\displaystyle i}$:te dimensionen.

En viktig skillnad mellan den endimensionella och den ${\displaystyle N}$-dimensionella oscillatorn är att den ${\displaystyle N}$-dimensionella oscillatorn har degenererade tillstånd, det vill säga flera olika tillstånd kan ha samma energi. Degenerationsgraden ges av

${\displaystyle g_{n}={\binom {N+n-1}{n}}}$

Notera att ${\displaystyle g_{0}=1}$ oavsett ${\displaystyle N}$, det vill säga grundtillståndet är aldrig degenererat.

Fördelningsfunktion

Sannolikheten för att ett tillstånd är besatt av en partikel ges av en fördelningsfunktion. Vid termisk jämvikt ges fördelningsfunktionen av Planckfördelningen, vilket är ett resultat av att den kvantharmoniska oscillatorn har jämnt fördelade energinivåer med konstanta avstånd. Den storkanoniska tillståndssumman ges av

${\displaystyle {\mathcal {Z}}=\sum _{N=0}^{\infty }\exp \left(-(E_{n}-N\mu )/k_{B}T\right)=\sum _{N=0}^{\infty }\exp \left(-(N\hbar \omega -N\mu )/k_{B}T\right)=\sum _{N=0}^{\infty }\exp \left((\mu -\hbar \omega )/k_{B}T\right)^{N}={\frac {1}{1-\exp \left((\mu -\hbar \omega )/k_{B}T\right)}}}$

Väntevärdet för hur många partiklar som har besatt ett tillstånd ges då av

${\displaystyle \langle N\rangle =k_{B}T{\frac {1}{\mathcal {Z}}}{\frac {d{\mathcal {Z}}}{d\mu }}={\frac {1}{\exp \left((\hbar \omega -\mu )/k_{B}T\right)-1}}}$

Detta samband gäller för varje energinivå och resulterar i Bose-Einstein-statistik. Om antalet partiklar inte är väldefinierat gäller att ${\displaystyle \mu =0}$ och Planckfördelningen erhålls

Planckfördelningen ${\displaystyle \langle N\rangle ={\frac {1}{\exp \left(\hbar \omega /k_{B}T\right)-1}}}$

Tillämpningar

Fotoner och fononer

Den kvantharmoniska oscillatorn används bland annat för att beskriva fotoner, fononer, magnoner och andra partiklar eller kvasipartiklar.

Se även

• Harmonisk oscillator

Källor

• Griffiths, David J. (2004). Introduction to Quantum Mechanics (andra upplagan). Prentice Hall. ISBN 978-0131118928 

Externa länkar

• Wikimedia Commons har media som rör Kvantharmonisk oscillator.
  Bilder & media