Histograma

Un histograma és una representació gràfica associada a una variable estadística contínua (o discreta amb molts valors diferents) per visualitzar les freqüències de les dades. Es construeix a partir d'una taula de freqüències o distribució de freqüències amb les dades agrupades en classes. Els histogrames més senzills, i que s'utilitzen més, són els que tenen totes les classes de la mateixa amplada,^[1] però a les aplicacions pràctiques també apareixen histogrames amb classes de diferent amplada.^[2][3] Malgrat la seva gran utilització, l'elecció del nombre de classes i l'amplada de les mateixes sovint és problemàtica. L'histograma és una de les Set Eines de la Qualitat.^[4]

Tipus d'histogrames i propietats

Histogrames amb classes (o intervals) d'igual amplada

Com a primer exemple, les següents dades són les notes d'un examen amb 20 estudiants:

La taula de freqüències d'aquestes dades és

Aquí s'ha utilitzat la notació habitual dels Intervals, on ${\displaystyle [0,2]}$ designa tots els nombres entre 0 i 2, inclosos 0 i 2; ${\displaystyle (2,4]}$ designa tots els nombres entre 2 i 4, exclòs el 2 i inclòs el 4, etc. Vegeu a la pàgina Taula de freqüències unes indicacions sobre aquest punt.

Un histograma d'aquestes dades consisteix en una representació gràfica on a l'eix d'abscisses hi ha les classes, i a sobre de cada classe es dibuixa un rectangle d'alçada proporcional a la freqüència de la classe. A la Figura 2 hi ha l'histograma corresponent a aquesta taula de freqüències absolutes. En lloc de les freqüències absolutes poden utilitzar-se les freqüències relatives, els percentatges, etc.; l'únic que canvia és l'escala vertical.

Histograma amb classes de diferent amplada

A la pràctica, molt sovint la taula de freqüències té classes de diferents amplades. Per exemple, la següent taula mostra la superfície (en ${\displaystyle m^{2}}$) dels habitatges de Catalunya l'any 2011^[5] que conté classes d'amplades 15, 30 i 120 ${\displaystyle m^{2}}$

${\displaystyle {\begin{array}{lrr}\hline {\mathit {Superf{\acute {\imath }}cie}}\ (m^{2})&{\mathit {Percentatge}}\\\hline ~~~[15,30]&~0,3\\~~~(30,45]&~3,6\\~~~(45,60]&14,4\\~~~(60,75]&22,7\\~~~(75,90]&27,4\\~~(90,105]&11,8\\(105,120]&~7,2\\(120,150]&~6,0\\(150,180]&~2,7\\(180,300]&~3,9\\\hline \mathbf {Total} &\mathbf {100} &\\\hline \end{array}}}$

La representació directa de les classes amb els rectangles proporcionals a la freqüència (vegeu la Figura 3) mostra una imatge distorsionada de les dades, ja que sembla que molts habitatges tinguin entre 180 i 300 ${\displaystyle m^{2}}$, mentre que aquesta classe només conté el 3,9 % dels habitatges. Això és a causa del fet que la impressió visual d'un rectangle depèn de l'àrea i no de l'alçada. El principi general de construcció dels histogrames^[3][2] és

Aplicant aquest principi, l'altura ${\displaystyle b_{i}}$ d'una classe amb amplada ${\displaystyle a_{i}}$ i freqüència absoluta ${\displaystyle F_{i}}$ és

on ${\displaystyle C}$ és una constant que determina l'escala vertical. Cal notar que si totes les classes tenen la mateixa amplada, llavors les altures dels rectangles queden proporcional a les freqüències, tal com s'ha fet a la secció anterior.

Si utilitzem freqüències relatives o percentatges (etc.) aleshores

on ${\displaystyle f_{1},\dots ,f_{k}}$ són les freqüències relatives i ${\displaystyle p_{1},\dots ,p_{k}}$són els percentatges. En aquesta secció prendrem ${\displaystyle C=1}$, ja que llavors les unitats de l'eix vertical de l'histograma són la freqüència absoluta (o freqüència relativa o percentatge, etc.) per unitat d'àrea.

A l'exemple dels habitatges, les unitats de l'eix vertical són el percentatge d'habitatges per ${\displaystyle m^{2}}$ de superfície i les altures dels rectangles són les següents:

A la Figura 4 hi ha l'histograma corresponent.

La fórmula (*) es dedueix de la següent manera: considerem una taula de freqüències (s'utilitza freqüències absolutes, però el raonament és anàleg amb freqüències relatives, percentatges, etc.), i designem per ${\displaystyle A_{1},\dots ,A_{k}}$ les àrees dels rectangles corresponents a les classes ${\displaystyle I_{1},\dots ,I_{k}}$ respectivament:

Per tal que la impressió visual sigui correcta volem que si, per exemple, la freqüència d'una classe és el doble que la d'una altra, l'àrea corresponent a la primera classe ha de ser el doble que la de la segona, això és,

Llavors,

Com que això valdrà per totes les classes, s'obté

D'on

$${\displaystyle A_{i}=C\,F_{i},\quad i=1,\dots ,k.}$$

${\displaystyle a_{i}}$

${\displaystyle I_{i}}$

${\displaystyle b_{i}}$

Elecció del nombre de classes

A la pràctica, sovint no és fàcil decidir el nombre de classes, ja que si s'utilitzen poques classes, s'amaguen les característiques de la variable, i, si se n'utilitzen moltes, llavors queden classes amb pocs elements. Tal com comenta Wilkinson"^[6] [l'histograma] és un dels gràfics més difícils de construir. Apareixen diversos problemes, entre ells, escollir el nombre de classes i decidir on posar els punts de tall".

La regla més antiga per calcular el nombre de classes, i una de les que encara s'utilitza més, és la regla de Sturges^[7] de 1926 (els paquets estadístics la utilitzen a menys que es digui una altra cosa): per a ${\displaystyle N}$ observacions, el nombre de classes recomanat ${\displaystyle k}$ és

L'argument de Sturges és que si es té, per exemple (utilitzant els seus nombres) 16 objectes, atès que ${\displaystyle 16=2^{4}}$, la manera més normal de repartir-los en grups és fent 5 grups de mides 1, 4, 6, 4, 1 (vegeu la Figura 5), que són els coeficients binomials ${\displaystyle {\binom {4}{0}},\,{\binom {4}{1}},\dots ,{\binom {4}{4}}}$. Més generalment, si tenim ${\displaystyle N=2^{r}}$ objectes, llavors, atès que

$${\displaystyle N=2^{r}=(1+1)^{r}=\sum _{i=0}^{r}{\binom {r}{i}},}$$

${\displaystyle r+1}$

$${\displaystyle \log _{2}N=\log _{2}2^{r}=r,}$$

Però diversos autors han argumentat que aquest nombre de classes pressuposa una distribució simètrica de les dades i, de forma subjacent, normalitat, i que si hi ha asimetria (vegeu més avall la secció sobre distribucions simètriques i asimètriques) cal prendre un nombre més gran d'intervals.^[8]

Una altra regla és la de Terrell and Scott:^[9]

que justifiquen sobre la base de propietats asimptòtiques.

També és important la regla de Scott:^[10]

on ${\displaystyle S}$ és una estimació de la desviació típica de la població, per exemple, la desviació típica modificada de les dades. Aquesta regla està calculada a partir d'una distribució normal, però Scott^[10] argumenta que també serveix per a distribucions més generals.

Amplada de les classes

El nombre de classes ${\displaystyle k}$ que s'ha calculat a l'apartat anterior es refereix inicialment a classes d'igual amplada. Per calcular aquesta amplada s'utilitza el rang de la distribució, que és la diferència entre l'observació més gran i la més petita, i que designarem per ${\displaystyle R}$:

$${\displaystyle R={\text{dada més gran}}-{\text{dada més petita}}.}$$

${\displaystyle a}$

$${\displaystyle a\approx {\frac {R}{k}}.}$$

Finalment, en molts casos, cal ajuntar diverses classes consecutives a l'esquerra i a la dreta per evitar que hi hagi classes buides o amb molt poques dades.

Histograma normalitzat o de densitat

Es diu que un histograma està normalitzat quan l'àrea total és 1; també es diu que és un histograma de densitat perquè és l'equivalent de la funció de densitat d'una variable aleatòria. Si s'utilitza les freqüències absolutes, aleshores les altures dels rectangles són:

$${\displaystyle b_{i}={\frac {F_{i}}{Na_{i}}},}$$

$${\displaystyle {\text{Àrea total}}=\sum _{i=1}^{k}A_{i}=\sum _{i=1}^{k}a_{i}b_{i}={\frac {1}{N}}\sum _{i=1}^{k}F_{i}=1.}$$

$${\displaystyle b_{i}={\frac {f_{i}}{a_{i}}}\quad {\text{o}}\quad b_{i}={\frac {p_{i}}{100\,a_{i}}}.}$$

L'histograma normalitzat permet comparar-lo amb la funció de densitat d'una variable aleatòria. A la Figura 6 hi ha representat l'histograma normalitzat de les notes de la primera secció, juntament amb la densitat d'una variable aleatòria normal amb mitjana i variància iguals a les de les notes.

Característiques de forma d'una distribució

Distribucions unimodals i multimodals

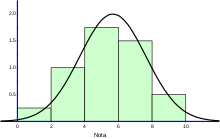
Cal recordar que la moda d'una distribució de freqüències és el valor de la variable que es repeteix més sovint, és a dir, la que té la freqüència més gran. Quan la variable és contínua (o discreta amb molts valors diferents) aleshores es parla de classe modal o interval modal com aquella classe que té la freqüència més gran. Les distribucions amb l'histograma com els de les Figures 2 i 4 que tenen forma de muntanya, ja que només tenen un màxim, o equivalentment, una sola moda, es diu que són unimodals. Les distribucions corresponents a histogrames com el de la Figura 1 que tenen forma de serralada, pel fet que tenen dos o més màxims locals, és a dir, tenen dues o més modes, es diu que són bimodals, trimodals, etc. En particular, la distribució de la Figura 1 és bimodal.

Distribucions simètriques i asimètriques (skewness)

En aquesta secció i la següent comentarem dues característiques més de la forma d'una distribució. Ens referirem només a distribucions unimodals.

L'histograma de la Figura 2 és aproximadament simètric, mentre que el de la Figura 4 és asimètric. Per mesurar el grau d'asimetria d'una distribució, Fisher va introduir el coeficient d'asimetria (en anglès, skewness):

$${\displaystyle g_{1}={\frac {\mu _{3}}{{\text{Var}}^{3/2}}},}$$

${\displaystyle \mu _{3}}$

$${\displaystyle \mu _{3}={\frac {1}{N}}\sum _{i=1}^{N}(x_{i}-{\overline {x}})^{3}={\frac {1}{N}}\sum _{i=1}^{k}(x_{i}-{\overline {x}})^{3}F_{i},}$$

$${\displaystyle {\overline {x}}={\frac {1}{N}}\sum _{i=1}x_{i}={\frac {1}{N}}\sum _{i=1}^{k}x_{i}F_{i}}$$

$${\displaystyle {\text{Var}}={\frac {1}{N}}\sum _{i=1}^{N}(x_{i}-{\overline {x}})^{2}={\frac {1}{N}}\sum _{i=1}^{k}(x_{i}-{\overline {x}})^{2}F_{i},}$$

Quan la distribució és perfectament simètrica, llavors ${\displaystyle g_{1}=0}$ .

Quan ${\displaystyle g_{1}>0}$ es diu que la distribució és asimètrica a la dreta, o esbiaixada a la dreta, com en el cas de les dades de l'histograma de la Figura 4, que ${\displaystyle g_{1}=2,13}$. Quan ${\displaystyle g_{1}<0}$ es diu que la distribució és asimètrica a l'esquerra, o esbiaixada a l'esquerra, com a la Figura 7.

La distribució de les notes de l'histograma de la Figura 2 tenen un coeficient d'asimetria ${\displaystyle g_{1}=-0,16}$, que vol dir que és lleugerament asimètric a l'esquerra.

Curtosi o apuntament

Tal com s'ha fet a la Figura 6, es pot comparar un histograma normalitzat amb una densitat normal amb la mateixa mitjana i variància que la variable estadística que s'estudiï. Si l'histograma normalitzat és més punxegut que la densitat normal (vegeu la Figura 8) es diu que la distribució de freqüències és leptocúrtica, en cas contrari (Figura 9) es diu que és platicúrtica, i si és aproximadament igual es diu que és mesocúrtica.

Per quantificar el grau de semblança amb l'apuntament de la distribució normal, Fisher va introduir el coeficient de curtosi o apuntament:

$${\displaystyle g_{2}={\frac {\mu _{4}}{{\text{Var}}^{2}}}-3,}$$

$${\displaystyle \mu _{4}={\frac {1}{N}}\sum _{i=1}^{N}(x_{i}-{\overline {x}})^{4}={\frac {1}{N}}\sum _{i=1}^{k}(x_{i}-{\overline {x}})^{4}F_{i}.}$$

${\displaystyle g_{2}}$

${\displaystyle X}$

${\displaystyle m}$

$${\displaystyle {\frac {E[(X-m)^{4}]}{{\big (}E[(X-m)^{2}]{\big )}^{2}}}=3.}$$

${\displaystyle g_{2}=0}$

${\displaystyle g_{2}>0}$

${\displaystyle g_{2}=0,74}$

${\displaystyle g_{2}<0}$

${\displaystyle g_{2}=-1,14}$

D'altra banda, per a qualsevol variable aleatòria (no constant, amb moment de 4t ordre finit) tenim ^[11] que ${\displaystyle \mu _{4}\geq {\text{Var}}^{2}}$, d'on ${\displaystyle \mu _{4}/{\text{Var}}^{2}\geq 1}$, i per tant,

$${\displaystyle g_{2}\geq -2.}$$

Histograma de freqüències acumulades

En un histograma de freqüències acumulades (absolutes o relatives, percentatges, etc.) es representen les freqüències acumulades; també s'anomena ogiva,^[12] però aquest terme també s'utilitza per al polígon de freqüències acumulades (vegeu la següent secció). La següent taula mostra les freqüències relatives acumulades de l'exemple de les 20 notes que hem comentat anteriorment:

L'histograma de freqüències relatives acumulades es mostra a la Figura 10.

Polígons de freqüències i ogives

Polígon de freqüències

El polígon de freqüències (relatives, absolutes, percentatges, etc.) d'una distribució de freqüències es construeix a partir de l'histograma corresponent ajuntant amb una línia poligonal simple els punts mitjans de les classes (que s'anomenen marques de classe).

Actualment, el seu principal interès és en l'estimació de densitats,^[13] i per aquest motiu ens restringirem a la utilització que allí se'n fa; així, només considerarem els polígons de freqüències relatives normalitzats, amb classes de la mateixa mida i on s'han ampliat el nombre de classes amb dues (de freqüència zero), a l'esquerra i dreta respectivament de les classes originals, i de la mateixa amplada que les altres (vegeu la Figura 11).

El polígon de freqüències així construït té una àrea total entre la línia poligonal i l'eix d'abscisses igual a 1^[14] i, llavors, tal com diu Scott, és una funció de densitat legítima (bona fide), ja que és una funció no negativa amb integral igual a 1.

Polígon de freqüències acumulades o ogiva

S'anomena polígon de freqüències acumulades o, tal com s'ha comentat a la secció anterior, ogiva,^[15] a una línia poligonal com la descrita a la Figura 12. La construcció gràfica a partir de l'histograma de freqüències acumulades és directe. Més concretament, a partir de la taula de freqüències relatives acumulades,

on ${\displaystyle fa_{j}}$ és la freqüència relativa acumulada de la classe ${\displaystyle j}$

$${\displaystyle fa_{j}=\sum _{i=1}^{j}f_{i},\ j=1,\dots ,k.}$$

${\displaystyle (c_{1},0),(c_{2},fa_{1}),(c_{3},fa_{2}),\dots ,(c_{k},fa_{k-1}),(c_{k+1},1)}$

${\displaystyle F}$

${\displaystyle x}$

${\displaystyle c_{1}}$

${\displaystyle c_{k+1}}$

$${\displaystyle F(x)\approx {\text{freq. relativa}}({\text{observacions}}\leq x),}$$

i, per tant, és l'equivalent a la funció de distribució d'una variable aleatòria.

Referències

Enllaços externs

• A Method for Selecting the Bin Size of a Histogram