Mitjana

S'ha proposat que «mitjana (matemàtiques)» sigui fusionat a aquest article. (Vegeu la discussió, pendent de concretar). Data: 2023

En estadística, el concepte de mitjana té dos significats estretament relacionats:

• El de mitjana aritmètica (que no és el mateix que la mitjana geomètrica o la mitjana harmònica)^[1]
• El d'esperança matemàtica d'una variable aleatòria

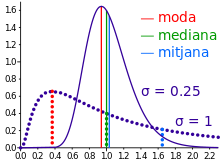
Hi ha altres mesures estadístiques que no s'han de confondre amb mitjanes, entre elles la mediana i la moda. Altres anàlisis estadístiques simples fan servir mesures de dispersió, com ara l'amplitud, l'amplitud interquartílica o la desviació tipus.

Per una variable aleatòria de valor real X, la mitjana és l'esperança de X. Cal notar que no totes les distribucions de probabilitat tenen una mitjana definida (o variància), com per exemple la distribució de Cauchy.

Per a un conjunt de dades, la mitjana és la suma de tots els valors dividida pel nombre de valors del conjunt. La mitjana d'un conjunt de dades ${\displaystyle x_{1},x_{2},...,x_{n}}$ es denota normalment com ${\displaystyle {\bar {x}}}$. Aquesta mitjana és un tipus de mitjana aritmètica. Si el conjunt de dades estigués basat en una sèrie d'observacions obtinguda pel mostreig d'una població estadística, llavors aquesta mitjana s'anomena mitjana mostral (${\displaystyle {\bar {x}}}$) per distingir-la de la mitjana poblacional ${\displaystyle \mu }$ o ${\displaystyle \mu }$_x).^[2][3] La mitjana se sol donar juntament amb la desviació tipus, ja que la primera descriu la localització central de les dades i la segona en descriu la dispersió. Una mesura alternativa de la dispersió és la desviació mitjana, que equival a la desviació absoluta mitjana de la mitjana: és menys sensible als valors extrems, però matemàticament no és tan amigable per tractar-la.

Si es pren una sèrie d'observacions com a mostra d'una població més gran (per exemple, agafant les alçades d'una mostra d'adults de la població mundial) o bé d'una distribució de probabilitat, llavors la població major es pot utilitzar per construir una "mitjana poblacional" que alhora és el valor esperat per la mostra extreta d'aquesta població. Per una població finita això seria simplement la mitjana aritmètica de la propietat en qüestió per a cada membre de la població; per una distribució de probabilitat, d'altra banda, seria la suma (o integral) sobre cada valor possible ponderat per la probabilitat d'aquest valor. És convenció universal representar la mitjana poblacional per ${\displaystyle \mu }$.^[4] En cas d'una distribució de probabilitat discreta, la mitjana d'una variable aleatòria discreta x s'obté agafant el producte de cada valor possible de x i la seva probabilitat P(x), i afegint tots aquests valors junts, donant ${\displaystyle \mu =\sum xP(x)}$.^[5]

La mitjana mostral pot diferir de la mitjana poblacional —especialment per mostres reduïdes—, però la llei dels grans nombres dicta que, com més gran és la mostra, més probable és que la mitjana mostral serà igual a la mitjana poblacional.^[6]

Les mitjanes també s'usen en camps diferents de l'estadística, com en geometria i anàlisi, per la qual cosa se n'han desenvolupat molts tipus, els quals es llisten a continuació.

Exemples de mitjanes

Mitjana aritmètica

La mitjana aritmètica és la mitjana "estàndard", i sovint se l'anomena simplement mitjana. Es calcula de la manera següent:^[1]

${\displaystyle {\bar {x}}={\frac {1}{n}}\cdot \sum _{i=1}^{n}{x_{i}}}$

No s'ha de confondre amb la mediana. La mitjana aritmètica d'un conjunt de dades no ha de ser per força el mateix valor que el valor del mig (la mediana) ni el que apareix més cops (el mode). Les distribucions asimètriques es descriuen millor amb la mitjana que no pas amb els altres estadístics (per exemple, la distribució exponencial o la distribució de Poisson).

Per exemple, la mitjana aritmètica dels sis valors 5, 10, 13, 7, 25 i 31 és:

${\displaystyle {\frac {5+10+13+7+25+31}{6}}={\frac {91}{6}}\approx 15}$

Mitjana geomètrica

La mitjana geomètrica és una mitjana útil per conjunts de nombres positius que són interpretats segons el seu producte i no pas segons la seva suma (com és el cas de la mitjana aritmètica). Per exemple, pot servir per taxes de creixement. El càlcul és el següent:^[7]

${\displaystyle {\bar {x}}=\left(\prod _{i=1}^{n}{x_{i}}\right)^{\tfrac {1}{n}}}$

Per exemple, la mitjana geomètrica dels sis valors 34, 27, 45, 55, 22 i 34 és

${\displaystyle (34\cdot 27\cdot 45\cdot 55\cdot 22\cdot 34)^{1/6}=1,699,493,400^{1/6}\approx 34.545}$

Mitjana harmònica

La mitjana harmònica és una mitjana útil per conjunts de nombres definits en relació a alguna unitat, com per exemple la velocitat (distància per unitat de temps). El seu càlcul és el següent:

${\displaystyle {\bar {x}}=n\cdot \left(\sum _{i=1}^{n}{\frac {1}{x_{i}}}\right)^{-1}}$

Per exemple, la mitjana harmònica dels sis valors 34, 27, 45, 55, 22 i 34 és

${\displaystyle {\frac {6}{{\frac {1}{34}}+{\frac {1}{27}}+{\frac {1}{45}}+{\frac {1}{55}}+{\frac {1}{22}}+{\frac {1}{34}}}}={\frac {60588}{1835}}\approx 33.0179836}$

Relació entre les mitjanes aritmètica, geomètrica i harmònica

Les mitjanes aritmètica (MA), geomètrica (MG) i harmònica (MH) satisfan aquestes desigualtats:

${\displaystyle MA\geq MG\geq MH\,}$

La igualtat es produeix només quan tots els elements de la mostra donada són iguals.

Mitjanes generalitzades

La mitjana generalitzada, també coneguda com a mitjana potencial o mitjana de Hölder, és una abstracció de les mitjanes aritmètica, quadràtica, geomètrica i harmònica. Es defineix sobre un conjunt de n nombres positius x_i segons:

${\displaystyle {\bar {x}}(m)=\left({\frac {1}{n}}\cdot \sum _{i=1}^{n}{x_{i}^{m}}\right)^{\tfrac {1}{m}}}$

Escollint el valor adequat pel paràmetre m s'obtenen totes les mitjanes:

${\displaystyle m\rightarrow \infty }$	màxim
${\displaystyle m=2}$	mitjana quadràtica
${\displaystyle m=1}$	mitjana aritmètica
${\displaystyle m\rightarrow 0}$	mitjana geomètrica
${\displaystyle m=-1}$	mitjana harmònica
${\displaystyle m\rightarrow -\infty }$	mínim

Mitjana-ƒ generalitzada

Això es pot generalitzar encara més fins a la mitjana-f generalitzada:

${\displaystyle {\bar {x}}=f^{-1}\left({{\frac {1}{n}}\cdot \sum _{i=1}^{n}{f(x_{i})}}\right)}$

I, de nou, escollint una ƒ invertible adequada donarà:

${\displaystyle f(x)=x}$	mitjana aritmètica
${\displaystyle f(x)={\frac {1}{x}}}$	mitjana harmònica
${\displaystyle f(x)=x^{m}}$	mitjana potencial
${\displaystyle f(x)=\ln x}$	mitjana geomètrica

Mitjana aritmètica ponderada

La mitjana aritmètica ponderada s'usa si es volen combinar els valors mitjans de mostres procedents de la mateixa població amb diferents mides mostrals:

${\displaystyle {\bar {x}}={\frac {\sum _{i=1}^{n}{w_{i}\cdot x_{i}}}{\sum _{i=1}^{n}{w_{i}}}}}$

Les ponderacions ${\displaystyle w_{i}}$ representen els límits de la mostra parcial.

Mitjana truncada

De vegades un conjunt de nombres pot contenir valors molt extrems, és a dir, molt més elevats o inferiors que els altres. Normalment se sol tractar de dades errònies causades per l'error experimental. La mitjana truncada, doncs, consisteix a descartar certes parts de les dades (les parts superior i inferior, normalment la mateixa quantitat als dos extrems) i després en fer la mitjana aritmètica de les dades restants. El nombre de valors extrets s'indica pel percentatge respecte al nombre total de valors.

Mitjana interquartílica

La mitjana interquartílica és un exemple específic de mitjana truncada: és simplement la mitjana aritmètica feta després de treure la quarta part de valors per sota i per sobre.

${\displaystyle {\bar {x}}={2 \over n}\sum _{i=(n/4)+1}^{3n/4}{x_{i}}}$

Mitjana d'una funció

En càlcul, i especialment en càlcul amb diverses variables, la mitjana d'una funció es defineix de manera general com el valor mitjà de la funció sobre el seu domini. Si només es té una variable, la mitjana d'una funció f(x) sobre un interval (a,b) es defineix per:

${\displaystyle {\bar {f}}={\frac {1}{b-a}}\int _{a}^{b}f(x)\,dx}$

Cal recordar que una propietat del valor mitjà ${\displaystyle {\bar {y}}}$ de molts nombres finits ${\displaystyle y_{1},y_{2},\dots ,y_{n}}$ és que ${\displaystyle n{\bar {y}}=y_{1}+y_{2}+\cdots +y_{n}}$. En altres paraules, ${\displaystyle {\bar {y}}}$ és el valor constant que, quan s'afegeix a ell mateix ${\displaystyle n}$ vegades, és igual al resultat d'afegir els ${\displaystyle n}$ termes de ${\displaystyle y_{i}}$. Anàlogament, una propietat del valor mitjà ${\displaystyle {\bar {f}}}$ d'una funció sobre l'interval ${\displaystyle [a,b]}$ és que ${\displaystyle \int _{a}^{b}{\bar {f}}\,dx=\int _{a}^{b}f(x)\,dx}$. En altres paraules, ${\displaystyle {\bar {y}}}$ és el valor constant que, quan s'integra sobre ${\displaystyle [a,b]}$, és igual al resultat d'integrar ${\displaystyle f(x)}$ sobre ${\displaystyle [a,b]}$. Però segons el segon teorema fonamental del càlcul, la integral d'una constant ${\displaystyle {\bar {f}}}$ és tan sols:

${\displaystyle \int _{a}^{b}{\bar {f}}\,dx={\bar {f}}x{\bigr |}_{a}^{b}={\bar {f}}b-{\bar {f}}a=(b-a){\bar {f}}}$

Vegeu també el primer teorema del valor mitjà per la integració, el qual garanteix que si ${\displaystyle f}$ és contínua llavors existeix un punt ${\displaystyle c\in (a,b)}$ tal que

${\displaystyle \int _{a}^{b}f(x)\,dx=f(c)(b-a)}$

El punt ${\displaystyle f(c)}$ s'anomena el valor mitjà de ${\displaystyle f(x)}$ sobre ${\displaystyle [a,b]}$; s'escriu, doncs, ${\displaystyle {\bar {f}}=f(c)}$, i es reordena l'equació precedent per aconseguir la definició de sobre.

Si es tenen múltiples variables, la mitjana en un veïnat d'un subespai relativament compacte U en un espai euclidià es defineix per:

${\displaystyle {\bar {f}}={\frac {1}{{\hbox{Vol}}(U)}}\int _{U}f}$

Això generalitza la mitjana aritmètica. D'altra banda, també és possible generalitzar la mitjana geomètrica per a funcions definint la mitjana geomètrica de f per

${\displaystyle \exp \left({\frac {1}{{\hbox{Vol}}(U)}}\int _{U}\log f\right)}$

De manera encara més general, en teoria de mesura i teoria de probabilitat els dos tipus de mitjana tenen gran importància. En aquest context, la desigualtat de Jensen estima la relació entre aquestes dues nocions diferents de la mitjana d'una funció. Finalment, cal notar que també existeixen la mitjana harmònica i la mitjana quadràtica (o valor eficaç) d'una funció.

Mitjana d'una distribució de probabilitat

Vegeu esperança matemàtica.

Mitjana d'angles

La majoria de les mitjanes més utilitzades no serveixen per quantitats circulars com angles, temps i fraccions de nombres reals. Per aquestes quantitats es necessita la mitjana de quantitats circulars.

Mitjana de Fréchet

La mitjana de Fréchet dona una manera per determinar el centre d'una distribució de masses en una superfície o, més generalment, en una varietat de Riemann. De manera diferent a altres mitjanes, la de Fréchet es defineix en un espai els elements del qual no han de poder necessàriament ser afegits els uns als altres o ser multiplicats per escalars. També es coneix aquesta mitjana per mitjana de Karcher.

Altres mitjanes

Propietats

Tots els tipus de mitjanes comparteixen algunes propietats. Algunes d'aquestes es llisten a continuació.

Mitjana ponderada

Una mitjana ponderada M és una funció que enllaça tuples de nombres positius amb nombres positius:

${\displaystyle M:(0,\infty )^{n}\to (0,\infty )}$

De tal manera que es mantenen les següents propietats:

• Punt fix: ${\displaystyle M(1,1,...,1)=1}$
• Homogeneïtat: ${\displaystyle M(\lambda \ x_{1},...,\lambda \ x_{n})=\lambda \ M(x_{1},...,x_{n})}$ per tot λ i x_i. En notació vectorial: ${\displaystyle M(\lambda \ x)=\lambda \ Mx}$ per tots els n-vectors x.
• Monotonia: si ${\displaystyle x_{i}\leq y_{i}}$ per tot i llavors ${\displaystyle Mx\leq My}$.

Segueix:

• Limitació: ${\displaystyle \min x\leq Mx\leq \max x}$
• Continuïtat: ${\displaystyle \lim _{x\to y}Mx=My}$
• Hi ha mitjanes que no són diferenciables.
• Totes les mitjanes llistades més amunt, amb l'excepció de la majoria de les mitjanes-f generalitzades, satisfan les següents propietats:
  • Si f és bijectiva, llavors la mitjana-f generalitzada satisfà la propietat de punt fix.
  • Si f és estrictament monòtona, llavors la mitjana-f generalitzada satisfà també la propietat de monotonia.
  • En general una mitjana-f generalitzada no té homogeneïtat.

Les propietats de sobre impliquen tècniques per a construir mitjanes més complexes:

Si C, M₁, ..., M_m són mitjanes ponderades i p és un nombre real positiu, llavors A i B definides per

${\displaystyle Ax=C(M_{1}x,\dots ,M_{m}x),}$

${\displaystyle Bx={\sqrt[{p}]{C(x_{1}^{p},\dots ,x_{n}^{p})}},}$

també són mitjanes ponderades.

Mitjana sense ponderar

Tal com es pot intuir, una mitjana sense ponderar equival a una mitjana ponderada amb el mateix pes per cada valor; una altra manera de dir-ho és que una ponderació homogènia permet canviar els paràmetres de ponderació sense que el resultat es vegi alterat.

Es defineix M, doncs, com una mitjana sense ponderar si és una mitjana ponderada que per cada permutació π dels pesos de ponderació el resultat és el mateix.

• Simetria: ${\displaystyle Mx=M(\pi x)}$ per totes les n-tuples π i permutacions π sobre n-tuples.

De manera anàloga a les mitjanes ponderades, si C és una mitjana ponderada, ${\displaystyle M_{1},...,M_{m}}$ són mitjanes sense ponderar, p és un nombre real positiu, llavors A i B definides per

${\displaystyle Ax=C(M_{1}x,\dots ,M_{m}x),}$

${\displaystyle Bx={\sqrt[{p}]{M_{1}(x_{1}^{p},\dots ,x_{n}^{p})}},}$

també són mitjanes sense ponderar.

Mitjanes poblacionals i mostrals

La mitjana d'una població té una esperança de μ, coneguda com la mitjana poblacional. La mitjana mostral és un bon estimador estadístic de la mitjana poblacional, ja que el seu valor esperat és el mateix que la mitjana poblacional. La mitjana mostral d'una població és una variable aleatòria no constant i, conseqüentment, té la seva pròpia distribució. Per una mostra aleatòria de n observacions d'una població distribuïda normalment, la distribució de la mitjana mostral és:

${\displaystyle {\bar {x}}\thicksim N\left\{\mu ,{\frac {\sigma ^{2}}{n}}\right\}}$

Sovint, com que la variància poblacional és un paràmetre desconegut, s'estima per la suma de quadrats mitjana, que canvia la distribució de la mitjana mostra d'una distribució normal a una distribució t de Student amb ${\displaystyle n-1}$ graus de llibertat.

Referències

Vegeu també

• Algorismes per calcular la variància
• Biaix d'un estimador
• Curtosi
• Estadística descriptiva
• Mediana
• Mitjana (estadística), el mateix que tendència central
• Moda

Enllaços externs

• Weisstein, Eric W., «Arithmetic Mean» a MathWorld (en anglès).
• Comparació entre la mitjana aritmètica i geomètrica (anglès)

Viccionari