Loi de probabilité

Vous lisez un « bon article » labellisé en 2012.

Pour les articles homonymes, voir Loi (homonymie) et Probabilité (homonymie).
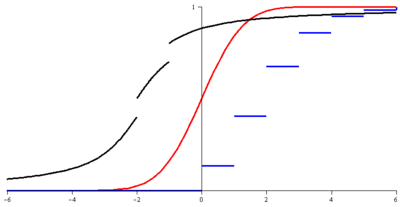  Représentation des fonctions de répartition de trois lois de probabilité :
|
En théorie des probabilités et en statistique, une loi de probabilité ou distribution de probabilité décrit le comportement aléatoire d'un phénomène dépendant du hasard. L'étude des phénomènes aléatoires a commencé avec l'étude des jeux de hasard. Jeux de dés, tirage de boules dans des urnes et jeu de pile ou face ont été des motivations pour comprendre et prévoir les expériences aléatoires. Ces premières approches sont des phénomènes discrets, c'est-à-dire dont le nombre de résultats possibles est fini ou infini dénombrable. Certaines questions ont cependant fait apparaître des lois à support infini non dénombrable ; par exemple, lorsque le nombre de tirages de pile ou face effectués tend vers l'infini, la distribution des fréquences avec lesquelles le côté pile apparaît s'approche d'une loi normale.
Des fluctuations ou de la variabilité sont présentes dans presque toute valeur qui peut être mesurée lors de l'observation d'un phénomène, quelle que soit sa nature ; de plus, presque toutes les mesures ont une part d'erreur intrinsèque. Les lois de probabilité permettent de modéliser ces incertitudes et de décrire des phénomènes physiques, biologiques, économiques, etc. Le domaine de la statistique permet de trouver des lois de probabilité adaptées aux phénomènes aléatoires.
Il existe beaucoup de lois de probabilité différentes. Parmi toutes ces lois, la loi normale a une importance particulière puisque, d'après le théorème central limite, elle approche le comportement asymptotique de nombreuses lois de probabilité.
Le concept de loi de probabilité se formalise mathématiquement à l'aide de la théorie de la mesure : une loi de probabilité est une mesure particulière, souvent vue comme la loi décrivant le comportement d'une variable aléatoire, discrète ou continue. Une mesure est une loi de probabilité si sa masse totale vaut 1. L'étude d'une variable aléatoire suivant une loi de probabilité discrète fait apparaître des calculs de sommes et de séries, alors que l'étude d'une variable aléatoire suivant une loi absolument continue fait apparaître des calculs d'intégrales. Des fonctions particulières permettent de caractériser les lois de probabilité, par exemple la fonction de répartition et la fonction caractéristique.
Définition informelle
Une loi de probabilité décrit de manière théorique le caractère aléatoire d'une expérience dont le résultat dépend du hasard[1],[2]. La notion d'« expérience aléatoire » est dégagée pour désigner un processus réel de nature expérimentale, où le hasard intervient, avec des issues possibles bien identifiées[3]. Par exemple, le lancer d'un dé ordinaire (équilibré) est une expérience aléatoire : le résultat est un chiffre entre 1 et 6, et chaque chiffre a la même chance d'apparaître ; la loi de probabilité de cette expérience aléatoire est donc : les six chiffres sont équiprobables, de probabilité 1/6.
Historiquement, les lois de probabilité ont été étudiées dans les jeux de hasard : jeux de dés, jeux de cartes, etc. Les résultats possibles d'un tel phénomène sont en nombre fini, sa loi de probabilité est dite discrète. Donner la loi de probabilité revient à donner la liste des valeurs possibles avec leurs probabilités associées[4]. Elle est alors donnée sous forme de formule, de tableau de valeurs, d'arbre de probabilité ou de fonctions (qui seront détaillées dans les sections suivantes).
Dans un contexte plus général, c'est-à-dire dans le cas où le nombre de valeurs possibles du phénomène aléatoire n'est pas fini mais infini (dénombrable ou non), la loi de probabilité décrit toujours la répartition des chances pour des résultats possibles mais est caractérisée par des fonctions (densité de probabilité et fonction de répartition, entre autres) ou plus généralement par des mesures.
Historique

L'utilisation du hasard existe depuis l'Antiquité, notamment dans les jeux de hasard, les paris sur les risques des transports maritimes ou les rentes viagères[5]. Cependant, une des premières références connues à des calculs de probabilités est un calcul élémentaire sur la Divine Comédie qui n'apparaît qu'au XVe siècle pendant la Renaissance[6]. Les premiers traités forment le début de la théorie des probabilités, principalement basée sur des probabilités combinatoires. Les problèmes se posent ainsi, à propos de la durée d'un jeu de cartes :
« Sur la durée des parties que l'on joue en rabattant... On demande combien il y a à parier que la partie qui peut durer à l'infini sera finie en un certain nombre déterminé de coups au plus. »
— Essay, de Montmort, 1713[7].
On reconnaît ici la probabilité (« à parier ») qu'une variable (« la durée de la partie ») soit plus petite qu'une valeur (« certain nombre déterminé ») ; il s'agit de la fonction de répartition de la loi de probabilité de la durée d'une partie.
C'est dans la thèse de Nicolas Bernoulli, publiée en 1711, qu'apparaît pour la première fois la loi uniforme[8]. Certaines autres lois font alors leur apparition, comme la loi binomiale ou la loi normale, même si leurs approches ne sont pas complètement rigoureuses[8]. Par exemple, la loi normale est construite par Abraham de Moivre grâce à la courbe de Gauss par une approximation numérique[9]. Au XVIIIe siècle, d'autres idées liées aux lois de probabilité émergent également[8], comme l'espérance d'une variable aléatoire discrète avec Jean le Rond D'Alembert ou les probabilités conditionnelles avec Thomas Bayes. Quelques lois de probabilité continues sont énoncées dans un mémoire de Joseph-Louis Lagrange en 1770[8].
L'utilisation rigoureuse des lois de probabilité se développe à partir du XIXe siècle dans des sciences appliquées, telles que la biométrie avec Karl Pearson[10] ou la physique statistique avec Ludwig Boltzmann[11].
La définition formelle des mesures de probabilités commence en 1896 avec une publication d'Émile Borel[12] et se poursuit avec plusieurs autres mathématiciens tels que Henri-Léon Lebesgue, René Maurice Fréchet, Paul Lévy et notamment Andreï Kolmogorov qui formule les axiomes des probabilités en 1933.
Définition mathématique
En théorie des probabilités, une loi de probabilité est une mesure dont la masse totale vaut 1. En particulier, cette mesure vérifie les trois axiomes des probabilités.
Définition[2] — Pour un espace mesurable, est une loi de probabilité, mesure de probabilité ou plus simplement probabilité si :
- est une application de dans [0,1] ;
- ;
- est -additive, c'est-à-dire pour toute famille finie ou dénombrable d'éléments deux à deux disjoints de :En particulier, .
Le triplet est appelé espace probabilisé. Une loi de probabilité est également appelée distribution de probabilité pour une étude plus appliquée[13].
Une manière usuelle d'expression d'une loi est l'utilisation d'une variable aléatoire puisque, pour toute loi de probabilité sur , il existe[14] une variable aléatoire définie sur un espace probabilisé (potentiellement différent de ) et de loi . Les lois les plus couramment étudiées en théorie des probabilités sont les lois à valeurs réelles ; elles peuvent être représentées à l'aide d'une variable aléatoire réelle par la définition suivante.
Définition[15] — Soit une variable aléatoire réelle sur l'espace probabilisé , c'est-à-dire une fonction mesurable .
La loi de probabilité de la variable aléatoire est la mesure de probabilité, notée , définie sur l'espace mesurable par :
pour tout borélien réel . Autrement dit, est la mesure image de par .
Ainsi, pour définir la loi d'une variable aléatoire, on transporte la loi de probabilité sur en une mesure sur .
La représentation d'une loi par une variable aléatoire n'est pas unique[16]. Autrement dit, deux variables aléatoires différentes, ou même définies sur des espaces différents, peuvent avoir la même loi. Deux variables aléatoires réelles et ont même loi si (en termes d'égalité de mesures). C'est-à-dire : pour tout . Le théorème suivant permet d'utiliser une autre caractérisation :
Théorème de transfert[14] (ou de transport[17]) — Soit une variable aléatoire réelle . Alors :
pour toute fonction telle qu'au moins une des deux intégrales ait un sens[18].
L'intégrale apparaissant dans le dernier terme est l'intégrale, au sens de la théorie de la mesure, de la fonction par rapport à la mesure . Cette intégrale prend la forme d'une somme dans le cas des lois discrètes.
Ainsi, deux variables aléatoires réelles et ont même loi si : pour toute fonction telle qu'au moins un des deux termes de l'égalité ait un sens.
Ce résultat est appelé law of the unconscious statistician (en) en anglais.
Loi multidimensionnelle

Intuitivement, une loi de probabilité est dite multidimensionnelle, ou n-dimensionnelle[19], si elle décrit plusieurs valeurs (aléatoires) d'un phénomène aléatoire. Par exemple lors du jet de deux dés, la loi de probabilité des deux résultats obtenus est une loi bidimensionnelle. Le caractère multidimensionnel apparaît ainsi lors du transfert, par une variable aléatoire, de l'espace probabilisé vers un espace numérique de dimension n. Dans l'exemple des deux dés, la dimension est n = 2 et l'espace est . La loi est également appelée loi jointe[20].
Un exemple important de loi multidimensionnelle est la loi de probabilité produit où et sont deux lois unidimensionnelles. Cette loi de probabilité est la loi d'un couple de variables aléatoires indépendantes[21], c'est le cas de l'exemple des deux dés.
Définition — Soit une variable aléatoire sur l'espace probabilisé , à valeurs dans muni de la tribu borélienne réelle produit . La loi de la variable aléatoire est la mesure de probabilité définie par pour tout :
La variable aléatoire est alors identifiée[22] à un vecteur aléatoire à n dimensions : . Le théorème de Cramer-Wold[23] assure que la loi (n-dimensionnelle) de ce vecteur aléatoire est entièrement déterminée par les lois (unidimensionnelles) de toutes les combinaisons linéaires de ses composantes : pour tous .

Cas d'une loi absolument continue
Une loi bidimensionnelle (ou n-dimensionnelle) est dite[24] absolument continue sur si la loi est absolument continue par rapport à la mesure de Lebesgue sur , c'est-à-dire si la loi de la variable aléatoire correspondante s'écrit sous la forme :
- pour tout
Lois marginales
Intuitivement, la loi marginale d'un vecteur aléatoire est la loi de probabilité d'une de ses composantes. Pour l'obtenir, on projette la loi sur l'espace unidimensionnel de la coordonnée recherchée. La loi de probabilité de la i-ème coordonnée d'un vecteur aléatoire est appelée la i-ème loi marginale[25]. La loi marginale de s'obtient par la formule :
- pour tout .
Les lois marginales d'une loi absolument continue s'expriment à l'aide de leurs densités marginales.
Loi conditionnelle

Intuitivement, une loi de probabilité conditionnelle permet de décrire le comportement aléatoire d'un phénomène lorsque l'on connaît une information sur ce processus. Autrement dit, la probabilité conditionnelle permet d'évaluer le degré de dépendance stochastique entre deux évènements[26]. Par exemple, lors d'un lancer de dés, la loi conditionnelle permet de donner la loi de la somme des résultats sachant que l'un des deux dés a donné un résultat d'au moins quatre.
Définition sur les évènements
La probabilité conditionnelle se définit[27], de manière la plus intuitive, sur les évènements par la probabilité d'un évènement A conditionnellement à un autre événement B. Pour tout A et B de la tribu sous-jacente tels que :
La loi de probabilité[28] est utilisée dans les probabilités et statistique élémentaires, pour la formule des probabilités totales ou le théorème de Bayes par exemple.
Définition pour les variables aléatoires
La probabilité conditionnelle est également définie pour les variables aléatoires. On étudie alors la loi d'une variable X conditionnellement à une variable Y. Lorsque , la loi de X sachant Y = y est définie par[28] :
Cependant cette définition n'est pas valide si la loi de Y est absolument continue puisque , pour tout y. La définition suivante est valide pour tout couple de variables aléatoires.
Définition[29] — Soit un couple de variables aléatoires réelles. Il existe une loi de probabilité , appelée loi conditionnelle de sachant , ou sachant , définie par, pour toute fonction borélienne bornée :
La loi est également notée ou . L'égalité précédente est une égalité entre variables aléatoires[30].
Définition pour les tribus
De manière plus générale, la loi de probabilité se définit à partir de l'espérance conditionnelle d'une variable aléatoire X sachant une tribu . Cette espérance conditionnelle est l'unique variable aléatoire -mesurable, notée et vérifiant[27] : pour toute Z, variable -mesurable. La loi conditionnelle est alors définie par[31] :
- où est la fonction indicatrice de .
Définition pour les lois absolument continues
Dans le cas des lois absolument continues, il existe une densité conditionnelle d'une loi par rapport à l'autre, et inversement. Si est la densité de la loi bidimensionnelle, les deux densités conditionnelles sont alors données par[32] :
- et .
Ici, et sont les deux lois marginales de X et Y respectivement. En remplaçant les intégrales par des sommes, on obtient des formules similaires dans le cas où les lois marginales sont discrètes ou lorsque la loi marginale de X est discrète et celle de Y est absolument continue, ou inversement[33].
Loi à valeurs dans un espace de Banach
Puisque est un espace de Banach, les lois à valeurs dans un espace de Banach généralisent les lois à valeurs réelles. La définition est alors similaire[34].
Définition — Soit une variable aléatoire sur l'espace probabilisé et à valeurs dans un espace de Banach muni de la tribu engendrée par les ensembles ouverts de . La loi de probabilité de la variable aléatoire est la mesure de probabilité définie sur l'espace mesurable par :
pour tout .
Pour obtenir de bonnes propriétés, il est courant de considérer des mesures de probabilités tendues, c'est-à-dire qui intuitivement sont concentrées sur un ensemble compact, et de supposer que l'espace de Banach est séparable[35].
Un exemple possible d'espace de Banach est l'espace des fonctions continues . Un processus stochastique est une famille de variables aléatoires indexées par un ensemble d'indices T. Une définition possible de la loi de probabilité d'un tel processus est la donnée des lois finies-dimensionnelles[36], c'est-à-dire la loi de probabilité multidimensionnelle des vecteurs lorsque . La loi peut alors être étendue par le théorème d'extension de Carathéodory pour le processus entier. Prenons l'exemple du mouvement brownien qui est à trajectoires continues, sa loi de probabilité est la mesure de Wiener[37], généralement notée W :
- , pour tout A sous-ensemble mesurable de .
Espace des lois de probabilité
Une loi de probabilité est une mesure de masse totale unitaire. L'ensemble des lois de probabilité est donc un sous-espace de l'espace des mesures finies. Cet espace est souvent noté[38] ou pour les lois de probabilité réelles. Dans la suite de cette section, les propriétés de cet espace sont détaillées pour les lois de probabilité réelles ; elles sont cependant vraies sur les espaces de Banach.
On peut munir cet espace d'une topologie appelée la topologie faible[38]. Cette topologie définit donc une convergence faible des lois de probabilité : une suite de lois de probabilité converge faiblement vers une loi de probabilité si :
- pour toute fonction continue bornée.
La convergence est notée[38] : . Cette convergence se répercute, par le théorème de transfert, sur les variables aléatoires de lois respectives ; la convergence de variables aléatoires est alors appelée convergence en loi (ou en distribution ou faible) et est notée ou . Si la convergence faible des variables aléatoires est souvent utilisée, elle ne concerne en fait que leur loi.
L'espace des lois de probabilité muni de cette topologie faible est[39] un espace métrique, complet et séparable (dans le cas d'un espace de Banach également séparable), ce qui en fait un espace polonais.
Propriétés
Paramètres et familles
Certaines lois sont regroupées par famille par rapport à certaines propriétés de leur densité ou de leur fonction de masse, ou suivant le nombre de paramètres qui les définissent, elles sont appelées famille paramétrique de lois de probabilité.
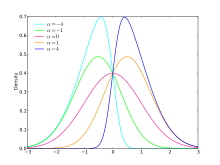

Paramètres
Les paramètres dits de position[40] influent sur la tendance centrale de la loi de probabilité, c'est-à-dire la ou les valeurs autour desquelles la loi prend ses plus grandes valeurs. L'espérance, la médiane, le mode, les différents quantiles ou déciles en sont des exemples.
Les paramètres dits d'échelle[40] influent sur la dispersion ou l'« aplatissement » de la loi de probabilité. La variance (ou le moment d'ordre deux), l'écart type et l'écart interquartile en sont des exemples.
Les paramètres dits de forme[40] sont les autres paramètres liés aux lois de probabilité. La queue ou traîne d'une loi de probabilité réelle fait partie de sa forme. Les queues de gauche et de droite sont[41] respectivement des intervalles du type et . Une loi de probabilité est dite à queue lourde si la mesure de probabilité de la queue tend moins vite vers 0, pour x allant à l'infini, que celle de la loi normale[42]. Notamment toute loi absolument continue, centrée, réduite dont la densité vérifie[43] :
est une loi à queues droite et gauche lourdes. L'asymétrie (ou moment d'ordre trois[44]) est un exemple de paramètre de forme, elle permet de rendre la queue de droite est plus ou moins lourde[45]. Le kurtosis (ou moment d'ordre quatre[44]) permet de favoriser ou de défavoriser les valeurs proches de la moyenne de celles qui en sont éloignées. Une loi de probabilité est dite mésokurtique, leptokurtique ou platikurtique si son kurtosis est nul, positif ou négatif.
Familles de lois
Une loi est dite de la famille exponentielle à un paramètre[46] si sa densité de probabilité ou sa fonction de masse ne dépend que d'un paramètre et est de la forme :
Cette famille regroupe beaucoup de lois classiques : loi normale, loi exponentielle, loi Gamma, loi du χ², loi bêta, loi de Bernoulli, loi de Poisson, etc.
Une loi est dite de la famille puissance à deux paramètres[46] et si sa densité est de la forme :
Loi directionnelle
Lorsqu'une loi de probabilité multidimensionnelle représente la direction aléatoire d'un phénomène, elle est dite loi directionnelle. Elle est alors la loi d'un vecteur aléatoire unitaire d-dimensionnel où ou, de manière équivalente, c'est une loi de probabilité sur la sphère d-dimensionnelle. Une loi directionnelle d-dimensionnelle peut alors être représenté par un vecteur (d-1-dimensionnel) en coordonnées polaires. Les lois de von Mises et de Bingham en sont des exemples[a 1].
Moments
S'il existe, le n-ième moment d'une loi de probabilité est défini par :
- .
Cette formule s'écrit[47] plus simplement dans le cas où la loi est définie à partir de la variable aléatoire .
Le premier moment, ou moment d'ordre 1, est également appelé l'espérance de la loi ; lorsque ce moment est nul, la loi est dite centrée. Le deuxième moment d'une loi centrée est également appelé la variance de la loi [48] ; lorsque ce moment vaut 1, la loi est dite réduite.
Certaines lois sont définies par un nombre fini de leur moments : la loi de Poisson est complètement définie par son espérance[49], la loi normale est complètement définie par ses deux premiers moments[50]; cependant, d'une manière générale, la collection de tous les moments d'une loi de probabilité ne suffit pas à caractériser cette dernière[51]. Certaines lois ne possèdent pas de moments, c'est le cas de la loi de Cauchy.
Entropie
Les lois de probabilité permettent de représenter des phénomènes aléatoires. L'entropie de Shannon d'une loi de probabilité a été introduite en thermodynamique pour quantifier l'état de désordre moléculaire d'un système[52]. Le but est de mesurer par une fonction le manque d'information de la loi de probabilité[53]. L'entropie a d'abord été définie pour les lois discrètes puis étendue pour les lois absolument continues. Pour une loi discrète et une loi de densité , l'entropie H est définie respectivement par[52],[54] :
- et .
- La loi normale est celle d'entropie maximale parmi toutes les lois possibles ayant même moyenne et même écart-type[11].
- La loi géométrique est celle d'entropie maximale parmi toutes lois discrètes de même moyenne[11].
- La loi uniforme continue est celle d'entropie maximale parmi les lois à support borné.
- La loi exponentielle est celle d'entropie maximale parmi les lois portées par et ayant la même moyenne[11].
- Les lois de la famille puissance, comme celle de Zipf, sont d'entropie maximale parmi celles auxquelles on impose la valeur du logarithme d'une moyenne.
L'état d'entropie maximale est l'état le plus désordonné, le plus stable et le plus probable d'un système[53]. Ces lois sont donc les moins prévenues de toutes les lois compatibles avec les observations ou les contraintes, et donc les seules admissibles objectivement comme distributions de probabilités a priori. Cette propriété joue un grand rôle dans les méthodes bayésiennes.
Classification des lois de probabilité sur la droite réelle
Les lois de probabilité les plus courantes dans les applications sont les lois dites discrètes et les lois dites absolument continues. Il existe cependant des lois de probabilité ni discrètes ni absolument continues.
Lois discrètes
Définition

Une loi de probabilité est dite concentrée[49] ou portée sur un ensemble si . Une loi de probabilité est dite discrète[13],[15] s'il existe un ensemble fini ou dénombrable sur lequel elle est concentrée.
Un élément est appelé un atome d'une loi de probabilité si le singleton et si . L'ensemble des atomes d'une loi de probabilité est fini ou dénombrable. Plus généralement, cette propriété est valable pour toute mesure σ-finie. Pour une loi de probabilité réelle, l'ensemble de ses atomes est exactement l'ensemble des points de discontinuité de sa fonction de répartition[55] ; dans ce cas, la finitude ou la dénombrabilité de l'ensemble des atomes se retrouve à partir du fait que la fonction de répartition est bornée[56].
Un critère suffisant pour qu'une loi soit discrète est que soit fini ou dénombrable.
Si est discrète, alors elle est concentrée en particulier sur l'ensemble (fini ou dénombrable) de ses atomes. Pour définir , il suffit alors de définir l'ensemble des couples[49] : , où est la fonction de masse de . On obtient ainsi :
- , pour tout ,
où est la mesure de Dirac[16],[24] au point .
Dans le cas où la loi de probabilité est définie à partir d'une variable aléatoire, les précédentes notions s'utilisent aussi pour cette variable aléatoire : une variable aléatoire est dite concentrée sur un ensemble , respectivement est dite discrète, si sa loi est concentrée sur , respectivement est discrète. De même, l'ensemble des atomes de est l'ensemble des atomes de .
Pour une variable aléatoire discrète , on obtient :
- , pour tout ,
où est la fonction de masse de , et la mesure de Dirac au point .
Pour une variable aléatoire discrète , le théorème de transfert s'exprime sous forme de sommes (ou de séries)[57] :
- , pour toute fonction positive ou nulle, ou telle que la série converge absolument.
La fonction de répartition d'une loi discrète est constante par morceaux[49]. Une loi discrète peut être représentée par un diagramme en bâtons[13].
Exemples
Voici une liste non exhaustive de lois de probabilité discrètes à support fini ou dénombrable.
Mesure de Dirac
La mesure de Dirac est la plus simple des lois discrètes au sens où le support de la loi ne contient qu'une valeur[58]. Si une variable aléatoire est de loi de Dirac , alors vaut avec une probabilité égale à 1. Cette loi modélise un phénomène déterministe (non aléatoire) puisque le résultat de l'expérience est (presque sûrement) égal à la valeur connue .
Loi uniforme discrète
La loi uniforme discrète modélise un phénomène aléatoire dont les résultats sont équiprobables, par exemple un lancer de dé. Si le support de la loi est l'ensemble à éléments distincts , alors cette loi est définie par :
Loi de Bernoulli
La loi de Bernoulli correspond à une expérience à deux issues (succès–échec), généralement codées respectivement par les valeurs 1 et 0, lors d'une expérience à deux issues et dont la probabilité de succès est . Cette loi dépend d'un paramètre mesurant la probabilité de succès. Une variable aléatoire à valeurs dans possède une loi de Bernoulli si :
- et .
Son univers image est .
Loi binomiale
C'est la loi du nombre de succès obtenus à l'issue de épreuves de Bernoulli indépendantes et de même paramètre , autrement dit c'est la loi de la somme de variables aléatoires indépendantes de loi de Bernoulli de même paramètre. Cette loi à support fini est définie par :
- , pour tout .
Son univers image est .
Distribution arithmétique
C’est une distribution concentrée sur un ensemble du type , où .
Loi géométrique
C'est la loi du numéro de l'épreuve amenant le premier succès lors d'une succession d'épreuves de Bernoulli indépendantes et de même paramètre . Elle peut ainsi modéliser le temps d'attente du premier succès dans une série d'épreuves de Bernoulli indépendantes à probabilité de succès . C'est l'unique loi discrète à posséder la propriété de perte de mémoire. Cette loi à support infini dénombrable est définie par :
- , pour tout .
Son univers image est .
Loi de Poisson
La loi de Poisson est la loi qui décrit le comportement du nombre d'évènements se produisant dans un laps de temps fixé lorsque l’écart entre deux évènements successifs suit une loi exponentielle, ce qui est le cas dans la plupart des applications. Cette loi à support infini dénombrable dépend d'un paramètre . Si est une variable aléatoire suivant une loi de Poisson, alors :
- , pour tout .
Son univers image est .
Loi hypergéométrique
La loi hypergéométrique est la loi suivie par le nombre de boules gagnantes extraites lors d'un tirage simultané de boules dans une urne contenant boules gagnantes et boules perdantes. Cette loi à support fini dépend de trois paramètres , et , et est définie par :
- , pour tout .
Lois absolument continues
Définitions

Une loi de probabilité réelle est dite absolument continue[59] ou à densité[24] lorsqu'elle est absolument continue par rapport à la mesure de Lebesgue.
Si est absolument continue alors en vertu du théorème de Radon-Nikodym[60], elle possède une densité de probabilité par rapport à la mesure de Lebesgue, c'est-à-dire qu'il existe[24] une unique (à égalité Lebesgue-presque partout près) fonction mesurable positive telle que pour tout :
où est la fonction caractéristique du borélien . Cette densité de probabilité n'a pas toujours d'expression analytique (voir les exemples ci-dessous).
Lorsqu'une loi de probabilité absolument continue est définie à partir d'une variable aléatoire , la variable aléatoire est dite absolument continue[16] ou à densité et la densité de la loi est également appelée la densité de , elle est parfois notée .
Pour une variable aléatoire absolument continue , le théorème de transfert s'écrit[61] à l'aide d'une intégrale de Lebesgue[59], pour toute fonction intégrable par rapport à ou positive ou nulle :
- .
La fonction de répartition d'une loi absolument continue est localement absolument continue, c'est une propriété nécessaire et suffisante. Une loi absolument continue ne possède pas d'atome[62]. Toutefois, cette propriété, qui oppose les lois absolument continues aux lois discrètes, n'est pas caractéristique des lois absolument continues mais des lois continues (voir la section Lois singulières ci-dessous).
Les lois absolument continues sont parfois appelées plus simplement lois continues[63]. C'est un abus de langage dû au fait que dans la plupart des applications en statistique, les lois continues sont absolument continues[64], mais ce n'est pas vrai dans le cas général.
Exemples
Loi uniforme
La loi uniforme sur un intervalle indique, intuitivement, que toutes les valeurs de l'intervalle ont les mêmes chances d'apparaître. Plus formellement, chaque sous-intervalle a une probabilité égale à la mesure de Lebesgue de (multipliée par une constante) d'apparaître. La loi uniforme ne dépend que de l'intervalle, son support est compact et sa densité est donnée par :
- pour .
- sinon.
Loi exponentielle
La loi exponentielle est la loi communément utilisée pour modéliser le temps de vie d'un phénomène puisque c'est l'unique loi absolument continue possédant la propriété de perte de mémoire. En ce sens elle est l'analogue continu de la loi géométrique. Cette loi à support semi-infini ne dépend que d'un paramètre (parfois appelé l'intensité), sa densité est donnée par, pour tout :
- .
Loi normale
La loi normale, ou loi gaussienne, est une loi centrale en théorie des probabilités et en statistique. Elle décrit le comportement des séries d'expériences aléatoires lorsque le nombre d'essais est très grand. C'est la loi limite dans le théorème central limite, elle est également l'unique loi stable de paramètre 2. La loi normale est caractérisée par sa moyenne (qui est également sa médiane) et par son écart-type, son support est la droite réelle. Sa densité est symétrique et sa forme est communément appelée la courbe de Gauss ou courbe en cloche :
Loi de Cauchy
La loi de Cauchy est la loi stable de paramètre 1, ce qui lui donne de bonnes propriétés. Elle est cependant un exemple typique de loi n'admettant pas de moments, en particulier ni moyenne, ni variance. Son support est la droite réelle et sa densité est symétrique et définie par :
- .
La loi de la position d'un mouvement brownien plan au moment où celui-ci atteint la droite est une loi de Cauchy[a 2].
Loi de Tukey-lambda
La loi de Tukey-lambda est une loi absolument continue, elle possède donc une densité de probabilité mais cette dernière n'a pas d'expression analytique. Cette loi dépend d'un paramètre, son support est soit un intervalle borné centré à l'origine, soit la droite réelle (en fonction du paramètre). La loi de Tuckey-lambda est définie à partir de sa fonction quantile (voir section Autres caractérisations ci-dessous) :
- .
Lois singulières
Définition
Une loi de probabilité est dite continue ou diffuse[55] lorsqu'elle ne possède pas d'atome.
En particulier, les lois absolument continues sont continues, la réciproque n'est cependant pas vraie. La fonction de répartition d'une loi de probabilité réelle continue est continue[55], c'est une propriété nécessaire et suffisante.
Une loi de probabilité est dite singulière lorsqu'elle est continue mais pas absolument continue. C'est-à-dire qu'une loi singulière ne possède ni atome, ni densité.
Ces notions se disent également pour les lois de probabilité définies à partir de variables aléatoires : une variable aléatoire est continue (ou diffuse), respectivement singulière, lorsque sa loi de probabilité associée est continue (ou diffuse), respectivement singulière.
Exemple

C'est une loi singulière. Elle est définie à partir de l'ensemble de Cantor : . Lorsque sont des variables indépendantes et identiquement distribuées de loi uniforme discrète sur , alors
est une variable aléatoire de loi de Cantor[65]. Cette loi de probabilité[66] s'écrit sous la forme , c'est la loi uniforme sur l'ensemble de Cantor. Sa fonction de répartition est l'escalier de Cantor, elle est dérivable presque partout et de dérivée nulle presque partout[65].
Dans les applications, il est rare que les lois continues contiennent une partie singulière[64]. L'ensemble de Cantor apparaît toutefois dans certains exemples bien connus : l'ensemble des zéros du mouvement brownien est un ensemble de type Cantor.
Autres cas
Il existe des lois de probabilité qui ne sont ni discrètes, ni absolument continues, ni singulières, elles sont parfois appelées lois mixtes[67],[68].
D'un point de vue plus général, toute loi de probabilité peut se décomposer[64],[56] en une combinaison linéaire d'une loi continue et d'une loi discrète . De plus le théorème de décomposition de Lebesgue appliqué[64] à indique que cette loi continue se décompose en une combinaison linéaire de deux lois continues, l'une est absolument continue par rapport à la mesure de Lebesgue et l'autre est singulière, étrangère à la mesure de Lebesgue. La décomposition s'écrit donc[69] :
avec et . La présence de assure que .

La loi de probabilité réelle suivante est un exemple de loi mixte obtenue en mélangeant une loi discrète, définie par ses atomes et sa fonction de masse , avec une loi absolument continue[64] de densité :
où . Sa fonction de répartition est une fonction continue par morceaux[70], mais pas constante par morceaux (ce qui est le cas des fonctions de répartition des lois discrètes).
Intuitivement, cela correspond à un phénomène aléatoire dont la loi est absolument continue. Cependant l'appareil de mesure ne peut mesurer les données qu'à partir d'un certain seuil c. Toutes les mesures non détectées par l'appareil seront assignées à 0, ainsi la loi est nulle sur toute partie « plus petite » que c alors qu'un saut apparaît au singleton c. Les mesures suivent la loi absolument continue pour les valeurs plus grandes que c[67]. Dans cet exemple la fonction de répartition est discontinue en c.
Caractérisations d'une loi de probabilité
Il existe plusieurs fonctions à variables réelles ou complexes qui déterminent de manière unique les lois de probabilité. Les propriétés de certaines de ces fonctions permettent de déduire des propriétés pour les lois comme le calcul des moments ou une expression de la convergence en loi.
À l'aide de la fonction de répartition

D'après le lemme de classe monotone, les ensembles , appelés pavés ou rectangles, engendrent[71] la tribu borélienne réelle et sont stables par intersection finie, il suffit alors de définir une loi de probabilité sur les pavés. On suppose que la loi de probabilité est réelle, c'est-à-dire .
La fonction de répartition d'une loi de probabilité réelle, notée par , est[72] la fonction définie par, pour tout :
Une loi de probabilité est caractérisée par sa fonction de répartition, c'est-à-dire que deux lois de probabilité sont égales si et seulement si leurs fonctions de répartitions sont égales[73].
Plus généralement, toute fonction croissante, continue à droite et vérifiant : et est la fonction de répartition d'une unique[74] loi de probabilité sur . La loi de probabilité définie à partir d'une fonction de répartition est appelée mesure de Lebesgue-Stieltjes[73].
Un des avantages de la fonction est qu'elle est bien définie pour toute loi de probabilité[74]. Cependant elle n'a pas toujours d'expression explicite, un exemple étant la fonction de répartition de la loi normale. La fonction de répartition permet parfois des calculs de lois aisés (loi du maximum ou du minimum d'un échantillon, par exemple) et fournit un critère commode[75] de convergence des lois de probabilité via le théorème porte-manteau.
À l'aide de la fonction caractéristique

On appelle fonction caractéristique d'une loi de probabilité , et l'on note , la « symétrie » de la transformée de Fourier de . Pour tout :
Suivant la définition de la transformée de Fourier, la fonction caractéristique est sa symétrique ou non[76]. Comme son nom l'indique, la fonction caractéristique détermine la loi de manière unique[77], c'est-à-dire que deux lois de probabilité sont égales si et seulement si leurs fonctions caractéristiques sont égales.
Un des avantages de la fonction caractéristique est qu'elle existe pour toute loi de probabilité[75],[76]. De plus, en utilisant la formule d'inversion de la transformée de Fourier[78], la loi de probabilité s'obtient à partir de la fonction caractéristique. La représentation des lois par la fonction caractéristique permet également de caractériser[79] la convergence des lois de probabilité via le théorème porte-manteau.
Dans le cas où la loi de probabilité est définie à partir d'une variable aléatoire , d'après le théorème de transfert, pour tout :
À l'aide de la fonction génératrice des moments
La fonction génératrice des moments d'une loi de probabilité , notée , est la « symétrie » de la transformée de Laplace de [65],[80]. Lorsque la fonction est intégrable par rapport à la mesure , pour tout :
La fonction génératrice des moments détermine la loi de probabilité de manière unique si cette fonction existe sur un intervalle contenant l'origine[75].
Un des avantages de cette fonction génératrice des moments est qu'elle permet de retrouver les moments de la loi de probabilité par les dérivées[80]. Pour tout , la -ième dérivée de la fonction génératrice des moments en 0 est le moment d'ordre de la loi de probabilité :
- .
La représentation des lois par la fonction génératrice des moments permet également de caractériser[75] la convergence des lois de probabilité via le théorème porte-manteau.
Dans le cas où la loi de probabilité est définie à partir d'une variable aléatoire , d'après le théorème de transfert, pour tout :
- .
De plus, pour des lois définies à partir de variables aléatoires, cette fonction permet aisément de montrer l'indépendance des variables[80].
Il existe un cas particulier pour les lois discrètes. La fonction génératrice des probabilités d'une loi de probabilité discrète est définie[80] comme l'espérance de la série génératrice : , sous réserve d’existence de cette série. Cette fonction génératrice détermine la loi de probabilité de manière unique[80].
Autres caractérisations

La fonction quantile[81] d'une loi de probabilité réelle , notée , est la fonction qui donne les quantiles de la loi. Elle est définie par[82], pour tout :
- ,
où est la fonction de répartition de .
Certaines lois de probabilité sont plus faciles à définir, via leur fonction quantile. Intuitivement, est la valeur telle qu'une proportion des valeurs possibles de la loi lui soit inférieure. , et sont respectivement le 1er quartile, la médiane[Information douteuse] et le 3e quartile de la loi.
Si est bicontinue alors est la fonction réciproque de la fonction de répartition[81] : ; c'est pour cela que dans le cas général on appelle aussi la fonction quantile réciproque généralisée de ou fonction inverse continue à droite de .
Cette fonction quantile détermine la loi associée[82] au sens où, si est une variable aléatoire de loi uniforme continue sur [0, 1], alors est une variable aléatoire de loi initiale. Cette représentation est particulièrement utile pour simuler des lois de probabilité[83] puisqu'il suffit alors de simuler une loi uniforme continue et d'y appliquer la fonction quantile (voir la section ci-dessous sur la simulation des lois de probabilité).
Certaines lois n'ont pas de fonction de répartition explicite mais sont définies à partir de leur fonction quantile, c'est le cas de la loi de Tukey-lambda.
Utilisations
La répartition statistique d'une variable au sein d'une population est souvent voisine des modèles mathématiques des lois de probabilité[84]. Il est souvent intéressant, pour des raisons théoriques et pratiques, d'étudier le modèle probabiliste, dit théorique[85]. L'étude commence alors par une sélection au hasard de plusieurs valeurs ou individus. Si la méthode utilisée est parfaite, c'est-à-dire que ces valeurs observées sont issues d'une sélection équiprobable[84], alors elles sont des variables aléatoires et l'étude du phénomène revient à étudier la loi de probabilité.
Simulation d'une loi de probabilité

Afin d'étudier les lois de probabilité, il est important de pouvoir les simuler, ceci est dû notamment à l’utilisation de l'informatique dans les sciences. Comme indiqué ci-dessus, les lois de probabilité sont caractérisées par la fonction quantile via une variable aléatoire de loi uniforme continue. Cette méthode générale comprend deux étapes[86] : la génération de valeurs dites pseudo-aléatoires de loi uniforme et l'inversion de la fonction de répartition de la loi étudiée. Cette deuxième étape n'est pas évidente à réaliser pour toutes les lois, d'autres méthodes sont alors utilisées.
|
Simulation de la loi uniforme
Pour obtenir des valeurs suivant la loi uniforme continue, l'ordinateur simule des valeurs de la loi uniforme discrète. Plusieurs méthodes ont été utilisées[87] : l'utilisation de tables de données qui pouvaient en contenir plus d'un million est de moins en moins utilisée ; l'utilisation de processus physique comme la création d'un bruit électronique est assez coûteuse pour la récupération des données ; l'utilisation d'algorithmes arithmétiques est la méthode la plus simple. Ces algorithmes étant déterministes (non aléatoires), les valeurs obtenues sont appelées pseudo-aléatoires. De nombreux algorithmes ont été créés pour améliorer l'indépendance entre les valeurs et leur répartition dans l'intervalle .
Simulation des autres lois
Lorsque la fonction de répartition est inversible, on utilise la caractérisation par la fonction quantile. Quelques exemples illustrent des cas où cette fonction n'est pas inversible : la méthode de Box-Muller permet de simuler la loi normale[88], la méthode de rejet de von Neumann est fondé sur un test statistique et est applicable pour plusieurs lois[89], d'autres méthodes spécifiques aux lois existent[90]. Pour une distribution à support fini, on peut utiliser la méthode des alias qui simule la distribution en temps constant.
Exemple
Une utilisation importante d'une simulation de loi de probabilité est la méthode de Monte-Carlo, pour faire des calculs approchés d’intégrales.
Par exemple pour approcher la valeur de π, la méthode consiste à simuler un grand nombre de valeurs suivant une loi uniforme continue sur et de compter la proportion des couples d'entre eux qui vérifient . Cette proportion se rapproche de lorsque le nombre de points tend vers l'infini[91].
Approximation d'une loi de probabilité

Plusieurs approximations d'une loi de probabilité existent en utilisant les différentes caractérisations détaillées ci-dessus. C'est généralement les techniques utilisées dans les cas pratiques. La première étape est la récolte des données, ce qui permet de construire les objets empiriques comme la fonction de répartition empirique. Ces derniers sont parfois appelés, par abus de langage, des lois de probabilité mais ce sont en fait des lois empiriques appelées distributions statistiques[84]. Des théorèmes limites ou des tests statistiques permettent finalement d'identifier la meilleure loi de probabilité qui modélise le phénomène aléatoire initial[85].
« Les probabilités doivent être regardées comme analogues à la mesure des grandeurs physiques, c'est-à-dire qu'elles ne peuvent jamais être connues exactement mais seulement avec une certaine approximation. »
— Émile Borel[92]
Par la fonction de répartition
Le test statistique de Kolmogorov-Smirnov, basé sur le théorème porte-manteau, permet d'identifier la fonction de répartition empirique calculée à partir des données à une fonction de répartition d'une loi de probabilité, en fonction d'un taux de rejet. L'avantage de la convergence des fonctions de répartition est que ces fonctions existent pour toutes lois de probabilité. Cette convergence permet en particulier d'approcher une loi absolument continue par une suite de lois discrètes[93].
Convergence des autres fonctions caractéristiques
Différents théorèmes de convergence de variables aléatoires permettent de construire une suite de lois de probabilité qui converge vers une loi donnée, ou inversement de construire une loi comme limite de lois de probabilité. Le théorème central limite concerne la loi normale pour loi limite. Le théorème de continuité de Paul Lévy concerne la convergence des fonctions caractéristiques.

Régression quantile
La régression quantile permet d'approcher les quantiles de la loi par les quantiles empiriques, c'est-à-dire calculés à partir d'éventuelles données. On peut utiliser un test statistique pour comparer les quantiles empiriques (observés) avec les quantiles de la loi qui est supposée modéliser le phénomène.
Cette approche est particulièrement utile pour étudier certaines lois qui ne sont pas connues explicitement par leur densité ou leur fonction de répartition mais par leurs quantiles, c'est le cas de la loi de Tukey-lambda.
Tests statistiques
Plusieurs tests statistiques existent pour comparer deux lois. Plus précisément, les tests d'adéquation permettent de comparer une loi empirique (c'est-à-dire calculée à partir des données issues d'échantillons) à une loi de probabilité dite a priori qui est censée modéliser le phénomène étudié. Les deux principaux tests sont : le test de Kolmogorov-Smirnov mentionné ci-dessus qui compare les fonctions de répartition et le test d'adéquation du χ² qui compare les effectifs observés en utilisant une loi du χ². Parmi ces tests, ceux qui concernent la loi normale sont dits tests de normalité.
Les tests d’homogénéité permettent de comparer deux lois empiriques pour savoir si elles sont issues du même phénomène ou, de manière équivalente, si elles peuvent être modélisées par la même loi de probabilité a priori. Ces tests comparent certaines propriétés des lois empiriques à la propriété de la loi a priori. Ils sont utiles dans la pratique puisqu'ils permettent de comparer non pas des lois entières mais des valeurs issues des lois[94] : le test de Fisher estime le rapport des variances empiriques via la loi de Fisher[94], le test de Student estime la moyenne empirique via la loi de Student[95], etc.
Exemples de modélisation
Les lois de probabilité sont utilisées pour représenter les phénomènes observés. Une loi de probabilité, dite a priori, est supposée modéliser les données récupérées, des tests statistiques sont alors réalisés pour affirmer ou infirmer la concordance de la loi de probabilité avec les données. Dans bien des domaines, les méthodes ont évolué et de meilleures lois de probabilité ont été créées afin de mieux correspondre au problème posé. Voici une liste d'exemples concrets qui proposent des modélisations :
- en économie : la bourse est une institution qui permet d'échanger des biens ou des titres. Afin de mieux estimer le prix futur d'un bien ou d'un titre, une étude de l'évolution historique de son prix est réalisée, notamment par la modélisation des variations des cours des prix. Ces variations ont d'abord été modélisées par une loi normale (Bachelier, 1900), puis une amélioration a été faite avec les lois stables de Pareto (Mandelbrot, 1963). Depuis, de nouveaux modèles sont toujours recherchés pour améliorer la perception des risques[a 3] ;
- aux jeux de hasard : pour jouer au loto français, il faut choisir six numéros parmi les quarante-neuf possibles. Si les joueurs choisissent leurs numéros au hasard, c'est-à-dire avec une loi uniforme discrète, alors le nombre de gagnants suit une loi de Poisson. Grâce à cette considération, une étude peut être réalisée puisque le nombre de gagnants est une donnée connue. Il apparaît que le choix n'est pas uniforme mais que les petits numéros ont été plus choisis[a 4] ;
- en maintenance : une bonne compréhension de la dégradation permet d'améliorer la performance de la maintenance. Plusieurs lois a priori ont été utilisées pour modéliser l'évolution de la fissure des chaussées : la loi exponentielle, la loi de Weibull, la loi log-normale, la loi log-logistique, etc. Pour une utilisation de la méthode du maximum de vraisemblance, la loi log-logistique fait partie des lois les plus adaptées[a 5] ;
- en médecine : pour tester l'efficacité des médicaments, un essai clinique est réalisé auprès d'un échantillon d'utilisateurs. Cette méthode fait partie de la théorie de la décision. Une des méthodes est de sélectionner un malade pour réaliser un test avec deux issues (succès ou échec), c'est-à-dire de modéliser par une loi de Bernoulli, puis de recommencer le plus de fois possibles ; c'est la méthode des urnes de Bernoulli. Une meilleure méthode est d'utiliser la loi hypergéométrique, ce choix permet de ne considérer qu'une population d'individus de taille fixée préalablement[a 6] ;
- en météorologie : en hydrologie, la pluviométrie est l'étude de la quantité d'eau issue de la pluie tombée en un point du sol pendant une durée de temps fixée. Le choix de la loi a priori ne fait pas consensus au sein de la communauté scientifique internationale. Certains auteurs préconisent l'utilisation de la loi log-normale qui s'ajuste bien aux petites valeurs. D'autres proposent la loi Gamma qui s'ajuste bien aux valeurs expérimentales. L'utilisation de la loi de Pareto a son intérêt pour représenter les valeurs moyennes[a 7].
Notes et références
- ↑ Wackerly, Mendenhall et Schaeffer 2008, p. 20.
- ↑ a et b Barbé et Ledoux 2007, p. 41.
- ↑ Henry 2001, p. 163.
- ↑ Wackerly, Mendenhall et Schaeffer 2008, p. 86.
- ↑ Henry 2001, p. 14.
- ↑ Dalang et Conus 2008, p. 127.
- ↑ Henry 2001, p. 34.
- ↑ a b c et d Dalang et Conus 2008, p. 128.
- ↑ Henry 2001, p. 42.
- ↑ Henry 2001, p. 54.
- ↑ a b c et d Caumel 2011, p. 137.
- ↑ Henry 2001, p. 55.
- ↑ a b et c Ruegg 1994, p. 35.
- ↑ a et b Ducel 1996, p. 8.
- ↑ a et b Saporta 2006, p. 16.
- ↑ a b et c Barbé et Ledoux 2007, p. 45.
- ↑ Barbé et Ledoux 2007, p. 54.
- ↑ Shiryaev 1995, p. 196.
- ↑ Shiryaev 1995, p. 160.
- ↑ Saporta 2006, p. 69.
- ↑ Saporta 2006, p. 22.
- ↑ Saporta 2006, p. 85.
- ↑ Saporta 2006, p. 87.
- ↑ a b c et d Ducel 1996, p. 9.
- ↑ Barbé et Ledoux 2007, p. 51.
- ↑ Ruegg 1994, p. 20.
- ↑ a et b Klebaner 2005, p. 44.
- ↑ a et b Barbé et Ledoux 2007, p. 150.
- ↑ Barbé et Ledoux 2007, p. 162.
- ↑ Barbé et Ledoux 2007, p. 160.
- ↑ Klebaner 2005, p. 46.
- ↑ Saporta 2006, p. 77.
- ↑ Saporta 2006, p. 80.
- ↑ Ledoux et Talagrand 2002, p. 37.
- ↑ Ledoux et Talagrand 2002, p. 38.
- ↑ Shiryaev 1995, p. 178.
- ↑ Klebaner 2005, p. 139.
- ↑ a b et c Ledoux et Talagrand 2002, p. 39.
- ↑ Ledoux et Talagrand 2002, p. 40.
- ↑ a b et c Ruppert 2004, p. 17.
- ↑ Ruppert 2004, p. 25.
- ↑ Ruppert 2004, p. 28.
- ↑ Ruppert 2004, p. 30.
- ↑ a et b Ruppert 2004, p. 26.
- ↑ Ruppert 2004, p. 24.
- ↑ a et b Wackerly, Mendenhall et Schaeffer 2008, p. 463.
- ↑ Shiryaev 1995, p. 182.
- ↑ La racine carrée de la variance est l'écart type, qui est une mesure de la dispersion des valeurs d'un échantillon statistique ou d'une distribution de probabilité.
- ↑ a b c et d Shiryaev 1995, p. 155.
- ↑ Shiryaev 1995, p. 234.
- ↑ Shiryaev 1995, p. 294.
- ↑ a et b Caumel 2011, p. 135.
- ↑ a et b Jedrzejewski 2009, p. 13.
- ↑ Caumel 2011, p. 136.
- ↑ a b et c Martiano 2006, p. 242.
- ↑ a et b Barbé et Ledoux 2007, p. 47.
- ↑ Martiano 2006, p. 157.
- ↑ Barbé et Ledoux 2007, p. 13.
- ↑ a et b Shiryaev 1995, p. 156.
- ↑ Barbé et Ledoux 2007, p. 31.
- ↑ Barbé et Ledoux 2007, p. 32.
- ↑ Ruegg 1994, p. 52.
- ↑ Saporta 2006, p. 18.
- ↑ a b c d et e Klebaner 2005, p. 36.
- ↑ a b et c Klebaner 2005, p. 37.
- ↑ Ledoux et Talagrand 2002, p. 22.
- ↑ a et b Bogaert 2006, p. 71.
- ↑ Caumel 2011, p. 80.
- ↑ Shiryaev 1995, p. 158.
- ↑ Bogaert 2006, p. 72.
- ↑ Shiryaev 1995, p. 144.
- ↑ Shiryaev 1995, p. 151.
- ↑ a et b Shiryaev 1995, p. 154.
- ↑ a et b Shiryaev 1995, p. 152.
- ↑ a b c et d Klebaner 2005, p. 38.
- ↑ a et b Saporta 2006, p. 55.
- ↑ Shiryaev 1995, p. 282.
- ↑ Saporta 2006, p. 57.
- ↑ Shiryaev 1995, p. 322.
- ↑ a b c d et e Saporta 2006, p. 60.
- ↑ a et b Bogaert 2006, p. 88.
- ↑ a et b Barbé et Ledoux 2007, p. 50.
- ↑ Barbé et Ledoux 2007, p. 49.
- ↑ a b et c Saporta 2006, p. xxviii.
- ↑ a et b Ruegg 1994, p. 37.
- ↑ Jedrzejewski 2009, p. 187.
- ↑ Jedrzejewski 2009, p. 182.
- ↑ Jedrzejewski 2009, p. 188.
- ↑ Jedrzejewski 2009, p. 189.
- ↑ Jedrzejewski 2009, p. 191.
- ↑ Jedrzejewski 2009, p. 215.
- ↑ Henry 2001, p. 194.
- ↑ Bogaert 2006, p. 70.
- ↑ a et b Saporta 2006, p. 340.
- ↑ Saporta 2006, p. 342.
Articles
- ↑ (en) K. V. Mardia, « Characterizations of directional distributions », Statistical Distributions in Scientific Work, vol. 3, , p. 365-385 (lire en ligne).
- ↑ [PDF] Michel Balazard, Éric Saiar et Marc Yor, « Note sur la fonction zeta de Riemann, 2 », Advances in Mathematics, vol. 143, , p. 284-287 (lire en ligne).
- ↑ [PDF] Michel Albouy et A. Sinani, « L'efficience des bourses de province françaises », Journal de la société statistique de Paris, vol. 122, no 4, , p. 200-214 (lire en ligne).
- ↑ [PDF] P. Roger et M.-H. Broihanne, « Les joueurs de loto français choisissent-ils leurs numéros au hasard? », Revue de statistique appliquée, vol. 54, no 3, , p. 83-98 (lire en ligne).
- ↑ [PDF] E. Courilleau et J. M. Marion, « Comparaison de modèles d'estimation de la fonction de survie appliquée à des données routières. », Revue de statistique appliquée, vol. 47, no 1, , p. 81-97 (lire en ligne).
- ↑ [PDF] F. Boutros-Toni, « L'analyse séquentielle exhaustive. Application en médecine. », Revue de statistique appliquée, vol. 29, no 4, , p. 31-50 (lire en ligne).
- ↑ [PDF] J. de Reffye, « Étude phénoménologique des précipitations pluvieuses. Modélisation mathématique des intensités de pluie en un point du sol. », Revue de statistique appliquée, vol. 30, no 3, , p. 39-63 (lire en ligne).
Voir aussi
Bibliographie
- Philippe Barbé et Michel Ledoux, Probabilité, Les Ulis, EDP Sciences, , 241 p. (ISBN 978-2-86883-931-2, lire en ligne).

- Patrick Bogaert, Probabilités pour scientifiques et ingénieurs : Introduction au calcul des probabilités, Paris, Éditions De Boeck, , 387 p. (ISBN 2-8041-4794-0, lire en ligne).

- Yves Caumel, Probabilités et processus stochastiques, Paris/Berlin/Heidelberg etc., Springer, , 303 p. (ISBN 978-2-8178-0162-9, lire en ligne).

- Dalang et Conus, Introduction à la théorie des probabilités, Lausanne, Presses polytechniques et universitaires romandes, , 204 p. (ISBN 978-2-88074-794-7, lire en ligne).

- Yves Ducel, Les probabilités à l'agrégation externe de mathématiques : Guide pour une révision, Besançon, Presses Universitaires de Franche-Comté, , 42 p. (ISBN 2-909963-08-X, lire en ligne).

- Michel Henry, Probabilités et statistique, Presses Universitaires de Franche-Comté, , 262 p. (lire en ligne).

- Franck Jedrzejewski, Modèles Aléatoires et Physique Probabiliste, Paris/Berlin/Heidelberg etc., Springer, , 572 p. (ISBN 978-2-287-99307-7, lire en ligne).

- (en) Fima Klebaner, Introduction to Stochastic Calculus With Applications, Imperial College Press, , 416 p. (ISBN 1-86094-555-4, lire en ligne).

- (en) Michel Ledoux et Michel Talagrand, Probability in Banach spaces : isoperimetry and processes, Berlin/Heidelberg/Paris etc., Springer, , 485 p. (ISBN 3-540-52013-9, lire en ligne).

- Jean-Jacques Martiano, Maths : Prépas commerciales, Principes, , 539 p. (ISBN 978-2-84472-828-9, lire en ligne).

- Alan Ruegg, Autour de la modélisation en probabilités, Presses Polytechniques et universitaires romandes, , 4e éd., 157 p. (ISBN 2-88074-286-2, lire en ligne).

- (en) David Ruppert, Statistics and Finance : An Introduction, Springer, , 485 p. (ISBN 0-387-20270-6, lire en ligne).

- Gilbert Saporta, Probabilités, Analyse des données et Statistiques, Paris, Éditions Technip, , 622 p. [détail des éditions] (ISBN 978-2-7108-0814-5, présentation en ligne).

- (en) Albert Shiryaev, Probability, Springer, , 2e éd., 627 p. (ISBN 978-0-387-94549-1, lire en ligne).

- (en) Dennis Wackerly, William Mendenhall et Richard L. Schaeffer, Mathematical Statistics with applications, Brooks Cole, , 7e éd., 922 p. (lire en ligne).

Articles connexes
- Théorie des probabilités
- Probabilité
- Probabilités (mathématiques élémentaires)
- Axiomes des probabilités
- Mesure (mathématiques)
- Loi de Gumbel
- Loi empirique
- Loi de probabilité marginale
- Probabilité conditionnelle
- Variable aléatoire
- Liste de lois de probabilité
- Avec grande probabilité
- Presque sûrement
Liens externes
- Ressource relative à la santé
 :
: - Medical Subject Headings
- Notice dans un dictionnaire ou une encyclopédie généraliste
 :
: - Store norske leksikon
- Notices d'autorité
 :
: - BnF (données)
- LCCN
- GND
- Japon
- Israël
- Tchéquie
v · m Index du projet probabilités et statistiques | |||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||
 Portail des probabilités et de la statistique
Portail des probabilités et de la statistique





















![{\displaystyle \mathbb {E} \left[\varphi (X)\right]{\stackrel {\text{déf.}}{=}}\int _{\Omega }\varphi {\big (}X(\omega ){\big )}\mathbb {P} (\mathrm {d} \omega )=\int _{\mathbb {R} }\varphi (x)\mathbb {P} _{X}(\mathrm {d} x),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4ad97bc026c84c768efe3c24a1fa90be1477713)


![{\displaystyle \mathbb {E} \left[\varphi (X)\right]=\mathbb {E} \left[\varphi (Y)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/885e7731a6347edc000195e769b173b3999cde23)





























![{\displaystyle \mathbb {E} \left[\varphi (X)|Y\right]=\int \varphi (x)\mathbb {P} _{X|Y}(\mathrm {d} x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7eaf8a0e5f85539c530ae8654d99a7c00e03091c)



![{\displaystyle \mathbb {E} \left[X|{\mathcal {G}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b047bb458622f35497bd0b378b3b1d82ec3c19a)
![{\displaystyle \mathbb {E} \left[Z\mathbb {E} (X|{\mathcal {G}})\right]=\mathbb {E} \left[ZX\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4a68f01eae65f27c2b7b93da93f785365810180)





























![{\displaystyle \left]-\infty ,x\right[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d1fe7a3c2bec379b123b3abe379a16729cabb9a9)









![{\displaystyle m_{n}=\mathbb {E} [X^{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/91cde357ac7466638096542ae55ceadddfd0bed6)












![{\displaystyle \{(\omega ,p(\omega ))\in \Omega _{a}\times ]0,1]\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/db8be31292fb88ffd029900198d992475308baa6)










![{\displaystyle \mathbb {E} \left[\varphi (X)\right]=\sum _{x\in \mathbb {R} _{a}}\varphi (x)\ p_{X}(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ba4e2a34cd458757b0c23ff0fb778c3785aa9a4a)





![{\displaystyle p\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33c3a52aa7b2d00227e85c641cca67e85583c43c)























![{\displaystyle \mathbb {E} \left[\varphi (X)\right]=\int _{\mathbb {R} }\varphi (x)f_{X}(x)\,\mathrm {d} x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3426601fcb58528af38fe8263c952f8751b12976)
![{\displaystyle \left[c,d\right]\subset \left[a,b\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5ae9069496f00ddb9ada019064530383bfc8abc7)
![{\displaystyle \left[c,d\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a1d8fbbc9f73f14f49a31914ad74c9e36a20a12)

![{\displaystyle x\in \left[a,b\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c4dd3adabf0430c82fd37cb45576a1df8c60002)

















![{\displaystyle \alpha ,\beta ,\gamma \in \left[0,1\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8e63b30e07aaa958969a4ef3a3f5dd95d6476848)




![{\displaystyle \alpha \in \left]0,1\right[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/52e48c2c2556c120c6d8d07d20f24a778ef8c8f4)
![{\displaystyle \left]-\infty ,x\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8de33d15a9fefbd6eafe1a3db13a4439dacf0859)




![{\displaystyle F(x)=\mathbb {P} {\big (}\left]-\infty ,x\right]{\big )}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f4231eca481e0de76f53ee43bb3bf705e87a5898)





![{\displaystyle \Phi _{X}(t)=\int _{\mathbb {R} }\mathrm {e} ^{\mathrm {i} tx}\,\mathbb {P} _{X}(\mathrm {d} x)=\int _{\Omega }\mathrm {e} ^{\mathrm {i} tX(\omega )}\,\mathbb {P} (\mathrm {d} \omega )=\mathbb {E} \left[\mathrm {e} ^{\mathrm {i} tX}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d8ab30c7b612196a03feaf60e34456621665846e)






![{\displaystyle M_{X}(t)=\int _{\mathbb {R} }\mathrm {e} ^{tx}\,\mathbb {P} _{X}(\mathrm {d} x)=\int _{\Omega }\mathrm {e} ^{tX(\omega )}\,\mathbb {P} (\mathrm {d} \omega )=\mathbb {E} \left[\mathrm {e} ^{tX}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c9ff25d0cc9030c9bd14689dafff0a413f7774dd)



![{\displaystyle p\in \left]0,1\right[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/93d00558eab93aa70de150faece10dc0ef6df8a6)








![{\displaystyle \left[0,1\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c57121c2b6c63c0b2f38eb96b1f7a543b5d1c522)
















