Estymator Kaplana-Meiera

Estymator Kaplana-Meiera – używany w statystycznej analizie przeżycia estymator prognozujący funkcję przeżycia. W badaniach medycznych może być użyty np. do przewidywania frakcji pacjentów, którzy przeżyją określony czas po operacji. Ekonomista może szacować czas jaki ludzie pozostają bezrobotni po utracie pracy. Inżynier może mierzyć czas do awarii urządzenia.

Wykres estymaty Kaplana-Meiera funkcji przeżycia składa się z szeregu poziomych odcinków, schodzących coraz niżej (funkcja schodkowa). Coraz większa próba statystyczna powoduje powstanie coraz większej liczby coraz krótszych odcinków, w granicy dążąc do prawdziwej funkcji przeżycia.

Przykład wykresu estymaty Kaplana-Meiera dla dwóch prób pacjentów

Ważną zaletą estymatora Kaplana-Meiera jest branie pod uwagę obserwacji cenzorowanych – braków danych od pewnego momentu czasu, różnego dla każdego obserwowanego obiektu (np. w przypadku odejścia pacjenta ze szpitala, utraty kontaktu z badanym itp.).

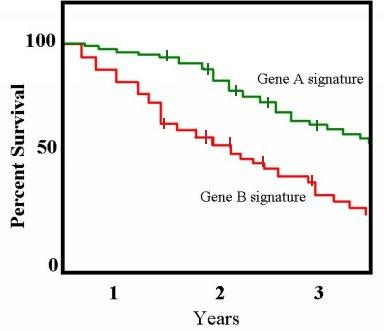
W statystyce medycznej typowe zastosowanie może obejmować podział pacjentów na grupy różniące się tylko jedną cechą, np. występowaniem określonego genu, albo podawaniem innego leku. Na wykresie pacjenci z grupy B umierają znacznie szybciej niż z grupy A. Po dwóch latach 80% pacjentów z grupy A ciągle żyje, a z grupy B mniej niż połowa.

Obliczanie

Niech S ( t ) {\displaystyle S(t)} będzie prawdopodobieństwem, że element populacji przeżyje co najmniej t . {\displaystyle t.} Uporządkujmy N {\displaystyle N} -elementową próbę z tej populacji według czasu przeżycia:

t 1 ⩽ t 2 ⩽ t 3 ⩽ … ⩽ t N . {\displaystyle t_{1}\leqslant t_{2}\leqslant t_{3}\leqslant \ldots \leqslant t_{N}.}

Z każdym t i {\displaystyle t_{i}} związana jest liczba n i {\displaystyle n_{i}} tych, o których wiemy, że dożyli do tego momentu oraz d i , {\displaystyle d_{i},} liczba śmierci w momencie t i . {\displaystyle t_{i}.} Warto zauważyć, że odległości pomiędzy kolejnymi momentami t i {\displaystyle t_{i}} zwykle nie będą stałe. Na przykład jeśli rozpatrujemy 10 przypadków, ze śmiercią w dniu 3, utratą kontaktu (obserwacja cenzorowana) w dniu 9 i kolejną śmiercią w dniu 11, to wówczas:

t 1 = 3 ,   n 1 = 10 ,   d 1 = 1 , {\displaystyle t_{1}=3,\ n_{1}=10,\ d_{1}=1,}
t 2 = 11 ,   n 2 = 8 ,   d 2 = 1. {\displaystyle t_{2}=11,\ n_{2}=8,\ d_{2}=1.}

Estymator Kaplana-Meiera to nieparametryczny estymator największej wiarygodności S ( t ) . {\displaystyle S(t).} Jest to iloczyn postaci:

S ^ ( t ) = ∏ t i < t n i − d i n i . {\displaystyle {\hat {S}}(t)=\prod \limits _{t_{i}<t}{\frac {n_{i}-d_{i}}{n_{i}}}.}

Alternatywną, używaną niekiedy definicją jest:

S ^ ( t ) = ∏ t i ⩽ t n i − d i n i . {\displaystyle {\hat {S}}(t)=\prod \limits _{t_{i}\leqslant t}{\frac {n_{i}-d_{i}}{n_{i}}}.}

Definicje różnią się tylko warunkiem na czas. W pierwszej estymator jest funkcją lewostronnie ciągłą, a w drugiej funkcją prawostronnie ciągłą.

Niech T {\displaystyle T} będzie zmienną losową mierzącą czas życia a F ( t ) {\displaystyle F(t)} jej dystrybuantą. Wówczas:

S ( t ) = P [ T > t ] = 1 − P [ T ⩽ t ] = 1 − F ( t ) . {\displaystyle S(t)=P[T>t]=1-P[T\leqslant t]=1-F(t).}

Stąd definicja z ciągłością prawostronną może być preferowana, gdy chcemy uzyskać prawostronnie ciągłą estymatę dystrybuanty.

Wariancja

Stworzono wiele różnych wzorów dla celów estymacji wariancji estymatora Kaplana-Meiera. Jednym z najczęściej używanych jest wzór Greenwooda:

Var ^ ( S ^ ( t ) ) = S ^ ( t ) 2 ∑ t i < t d i n i ( n i − d i ) . {\displaystyle {\widehat {\operatorname {Var} }}({\widehat {S}}(t))={\widehat {S}}(t)^{2}\sum \limits _{t_{i}<t}{\frac {d_{i}}{n_{i}(n_{i}-d_{i})}}.}

Porównywanie estymat

W niektórych przypadkach potrzebne jest porównanie dwóch różnych krzywych przeżycia otrzymanych z estymatora Kaplana-Meiera. Można to zrobić na wiele sposobów, w szczególności:

  • test Coxa
  • test Coxa-Mantela
  • logarytmiczny test rang (ang. log-rank test)
  • uogólnienie Gehana testu Wilcoxona
  • uogólnienie Peto i Peto testu Wilcoxona.

Bibliografia

  • Kaplan E.L., Meier Paul, „Nonparametric estimation from incomplete observations”. J. Am. Stat. Assoc. 53, s. 457–481 (1958).
  • Kaplan E.L na temat tej pracy w „This week’s citation classic”. Current Contents 24, s. 14 (1983). Dostępne w UPenn jako PDF.
  • Greenwood M., The natural duration of cancer. Reports on Public Health and Medical Subjects. London: Her Majesty’s Stationery Office 1926; 33: s. 1–26.

Linki zewnętrzne

  • Przykład estymacji Kaplana-Meiera w czasie rzeczywistym w Javie (ang.)
  • Obliczanie krzywych Kaplana-Meiera autorstwa Steve Dunn. cancerguide.org. [zarchiwizowane z tego adresu (2019-06-17)]. (ang.).
  • Kalkulator MTBF (ang.)