Funkcja wiarygodności

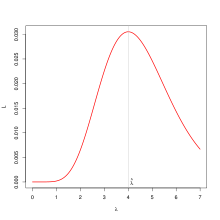
Funkcja wiarygodności (wiarygodność) – w statystyce, funkcja parametru modelu i próby losowej, która jest proporcjonalna do prawdopodobieństwa zaobserwowania próby o konkretnej postaci przy różnych parametrach modelu. Wyraża „wiarygodność” wartości parametru w obliczu danych. Odgrywa kluczową rolę we wnioskowaniu statystycznym^[1]. Jej nazwę wprowadził Ronald Fisher w 1922^[2].

Definicja

Najbardziej ogólna postać funkcji wiarygodności ${\displaystyle L(H_{\theta }),}$ zapisywanej także jako ${\displaystyle L(H_{\theta }|D)}$ lub z użyciem symbolu ${\displaystyle {\mathcal {L}},}$ to^[1]:

${\displaystyle L(H_{\theta }|D)=K\times P(D|H_{\theta }),}$

gdzie ${\displaystyle K}$ to arbitralna dodatnia stała proporcjonalności wynikająca ze specyficzności przyjętego modelu, ${\displaystyle H_{\theta }}$ to reprezentujący różne hipotezy wektor zmiennych wartości parametru ${\displaystyle \theta ,}$ a ${\displaystyle D}$ to stały, dany wektor obserwacji. ${\displaystyle P}$ to funkcja gęstości lub masy prawdopodobieństwa, dla przyjętego modelu statystycznego^[1][3].

Realizacja funkcji wiarygodności dla wektora obserwacji ma z reguły dla danych iid formę typu^[4]:

${\displaystyle L(H_{\theta })=\prod _{i=1}^{n}P(x_{i}|\theta ).}$

Wiarygodność to, w uproszczeniu, prawdopodobieństwo parametru w konkretnym kontekście ustalonych obserwacji i modelu. Ma podobną postać do prawdopodobieństwa danych dla parametru (czyli funkcji gęstości lub masy), ale przyjmuje odwrotnie to, który czynnik jest losowy, a który stały^[1][2].

Interpretacja

Interpretacja wiarygodności ma sens tylko z zachowaniem kontekstu; bardziej przyjaznym wskaźnikiem jest iloraz wiarygodności, który wskutek dzielenia pozbawiony jest stałej ${\displaystyle K}$ reprezentującej specyfikę modelu^[1].

Oszacowanie wiarygodności nie jest jednak samo w sobie wyczerpującą podstawą do osądzania prawdziwości hipotez. Sam fakt, że jedno wyjaśnienie jest dużo bardziej prawdopodobne od alternatywnego, w oderwaniu od dodatkowych wskaźników i rozumowania, nie jest wyczerpująco diagnostyczny. Ilustruje to problem błędu rozumowania prokuratorskiego, takiego jak sprawa Sally Clark, matki dwójki dzieci, które zmarły z rozpoznaniem nagłej śmierci łóżeczkowej. Po śmierci drugiego dziecka została oskarżona o morderstwo i skazana w 1999, w dużej mierze w oparciu o zeznania profesora pediatrii, który oszacował szansę na dwukrotne wystąpienie bardzo rzadkiej w populacji przyczyny śmierci przypadkiem na bardzo małą. Proces ściągnął na Clark dużą antypatię opinii publicznej. Została uniewinniona na podstawie nowo ujawnionych dowodów w 2003, popadła jednak w alkoholizm i zmarła w 2007 w wieku 43 lat, osieracając jedno żyjące dziecko. Sposób argumentacji statystycznej przedstawionej w trakcie procesu był potem głęboko krytykowany jako tragiczne nadużycie^[5][6].

Prawo wiarygodności

Pojęcie wiarygodności może być pomocne we wnioskowaniu w przypadku porównywania dwóch hipotez. Zgodnie z prawem wiarygodności, jeżeli obie są zgodne z dostępnymi danymi, większe poparcie w danych ma hipoteza o większej wiarygodności^[7]. Porównując wiarygodności można nie tylko wskazać, która z hipotez ma lepsze poparcie, ale możliwe jest również mierzenie tego poparcia dzięki ilorazowi wiarygodności^[8].

Zastosowania

Wiarygodność jest wykorzystywana we wszystkich głównych podejściach do wnioskowania statystycznego (np. częstościowym czy bayesowskim). Część statystyków preferuje odrębne podejście oparte wręcz wyłącznie na ilorazach wiarygodności^[1].

Ponieważ wiarygodność jest z reguły używana w postaci ilorazów, często wyraża się ją w postaci logarytmu naturalnego. Jest on także łatwiejszy w maksymalizacji, co wykorzystuje metoda największej wiarygodności w estymacji^[1].

Iloraz wiarygodności

Iloraz wiarygodności, zapisywany z reguły przy pomocy symbolu ${\displaystyle \Lambda ,}$ to:

${\displaystyle \Lambda (\theta _{1}:\theta _{2}\mid x)={\frac {L(\theta _{1}\mid x)}{L(\theta _{2}\mid x)}}.}$

Wiele testów statystycznych opiera się o – poprzedzone wyborem odpowiedniego (lub nie) modelu, definiującego ${\displaystyle P}$ – porównanie wiarygodności dwóch hipotez. Takie porównanie jest częścią lematu Neymana-Pearsona, i było ważnym historycznym źródłem kształtującym testy w podejściu częstościowym. W statystyce bayesowskiej miary tego typu noszą nazwę czynnika Bayesa^[1].

Przypisy