Krzywa eliptyczna

Niektóre z zamieszczonych tu informacji wymagają weryfikacji. Uwagi: dużo błędów zostało zakomentowanych w kodzie strony. Po wyeliminowaniu niedoskonałości należy usunąć szablon {{Dopracować}} z tego artykułu.

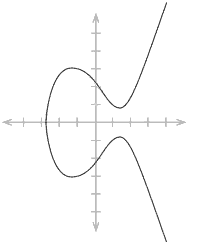
Krzywa eliptyczna – pojęcie z zakresu geometrii algebraicznej, oznaczające według współczesnej definicji gładką krzywą algebraiczną (czyli rozmaitość algebraiczną wymiaru 1) o genusie równym 1 wraz z wyróżnionym punktem ${\displaystyle O,}$ zwanym „punktem w nieskończoności”. Elementy krzywej rozumianej jako zbiór nazywa się, zgodnie z terminologią geometryczną, punktami.

Dowodzi się, że każda krzywa eliptyczna jest rozmaitością abelową – można na niej zdefiniować w sensowny (zgodny z własnościami geometryczno-algebraicznymi) sposób operację grupową („dodawanie” punktów), dla której ${\displaystyle O}$ jest elementem neutralnym.

Można również pokazać, że każdą krzywą eliptyczną nad dowolnym ciałem ${\displaystyle K}$ można zapisać w postaci równania

${\displaystyle y^{2}+a_{1}xy+a_{3}y=x^{3}+a_{2}x^{2}+a_{4}x+a_{6}}$

dla pewnych stałych ${\displaystyle a_{k}\in K,}$ gdzie ${\displaystyle x,}$ ${\displaystyle y}$ to współrzędne punktów na płaszczyźnie ${\displaystyle K^{2}.}$ Reprezentacja taka z reguły nie jest jednoznaczna. W szczególnych przypadkach definicję tę można znacznie uprościć. Równanie to przedstawia tzw. model afiniczny krzywej eliptycznej.

Postać normalna krzywej

W przypadku, gdy charakterystyka ciała ${\displaystyle K}$ jest inna, niż 2 i 3 (czyli, w szczególności, np. jeśli krzywa jest zdefiniowana nad ciałem liczb zespolonych), równanie afiniczne krzywej można uprościć do postaci

${\displaystyle y^{2}=x^{3}+Ax+B,A,B\in K}$

nazywanej równaniem (postacią) Weierstrassa.

Dla ciała charakterystyki 3 najbardziej ogólną postacią równania jest

${\displaystyle y^{2}=4x^{3}+b_{2}x^{2}+2b_{4}x+b_{6}.}$

Zastosowania

Dzięki zastosowaniu krzywych eliptycznych udało się rozwiązać jeden z najstarszych problemów matematycznych: przeprowadzić dowód wielkiego twierdzenia Fermata^[1]. Problem ten pozostawał nierozwiązany przez ponad 300 lat, zaś jego rozwiązanie podał Wiles w roku 1993, korzystając właśnie z pojęć z zakresu krzywych eliptycznych. Dowód jednak zawierał luki, które wraz ze współpracownikami Wilesowi udało się usunąć w roku 1994.

Jednym z kluczowych zastosowań krzywych eliptycznych współcześnie jest kryptografia.

 Osobny artykuł: Kryptografia krzywych eliptycznych.

Zobacz też

Zobacz multimedia związane z tematem: Krzywa eliptyczna

• funkcje eliptyczne
• kryptografia krzywych eliptycznych

Przypisy

Linki zewnętrzne

• Eric W.E.W. Weisstein Eric W.E.W., Elliptic Curve, [w:] MathWorld, Wolfram Research [dostęp 2020-12-12]  (ang.).
• Jennifer Balakrishnan, E is for Elliptic Curves (ang.), Oxford University Mathematical Institute, maths.ox.ac.uk, 19 sierpnia 2022 [dostęp 2023-05-29].