Antiprismă

Antiprisme n-gonale uniforme
Antiprismă hexagonală
Descriere
Tip	poliedru uniform în sensul de poliedru semiregulat
Fețe	2 n-goane, 2n triunghiuri
Laturi (muchii)	4n
Vârfuri	2n
χ	2
Configurația vârfului	3,3,3,n
Simbol Schläfli	{ }⊗{n}[1] s{2,2n} sr{2,n}
Simbol Conway	An
Diagramă Coxeter
Grup de simetrie	Dnd, [2+,2n], (2*n), ordin 4n
Grup de rotație	Dn, [2,n]+, (22n), ordin 2n
Poliedru dual	trapezoedru n-gonal dual uniform
Proprietăți	Convexe, cu fețe poligoane regulate, tranzitiv pe fețe
Desfășurată

În geometrie, o antiprismă n-gonală este un poliedru compus din două copii paralele ale unui poligon cu n laturi, conectate printr-o bandă de triunghiuri alternante. Antiprismele sunt o subclasă de prismatoide și sunt un tip (degenerat) de poliedre snub.

Antiprismele sunt similare cu prismele, cu excepția faptului că bazele sunt rotite una față de alta și că fețele laterale sunt triunghiuri în loc de patrulatere.

În cazul unei baze regulate cu „n” laturi, de obicei se ia în considerare cazul în care copia sa este rotită cu un unghi de ${\displaystyle 180^{\circ }/n\,}$. O regularitate suplimentară se obține atunci când linia care leagă centrele bazelor este perpendiculară pe planele bazelor, făcând-o o antiprismă dreaptă. Ca fețe are cele două baze n-gonale și, conectate la aceste baze, 2n triunghiuri isoscele.

Antiprisme uniforme

O antiprismă uniformă are, în afară de fețele de bază, 2n triunghiuri echilaterale ca fețe. Antiprismele uniforme formează o clasă infinită de poliedre tranzitive pe vârfuri, la fel cu prismele uniforme. Pentru n = 2 se obține tetraedrul regulat ca antiprismă digonală (antiprismă degenerată), iar pentru n = 3 octaedrul regula ca antiprismă triunghiulară (antiprismă nedegenerată).

Poliedrele duale ale antiprismelor sunt trapezoedrele. Existența lor a fost discutată și numele lor a fost inventat de Johannes Kepler, deși este posibil ca acestea să fi fost cunoscute anterior de Arhimede, întrucât îndeplinesc aceleași condiții pe vârfuri ca și poliedrele arhimedice.

Familia antiprismelor n-gonale uniforme     v • d • m
Imagine poliedru												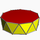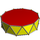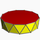...	Antiprismă apeirogonală
Imagine pavare sferică												Imagine pavare plană
Configurația vârfului n.3.3.3	2.3.3.3	3.3.3.3	4.3.3.3	5.3.3.3	6.3.3.3	7.3.3.3	8.3.3.3	9.3.3.3	10.3.3.3	11.3.3.3	12.3.3.3	...	∞.3.3.3

Diagrame Schlegel

Diagrame Schlegel ale antiprismelor

A3

A4

A5

A6

A7

A8

Coordonate carteziene

Coordonatele carteziene ale vârfurilor unei antiprisme drepte cu baze n-gonale (regulate) și triunghiuri isoscele sunt

${\displaystyle \left(\cos {\frac {k\pi }{n}},\sin {\frac {k\pi }{n}},(-1)^{k}h\right)}$

unde k poate lua valori între 0 și 2n − 1; dacă triunghiurile sunt echilaterale,

${\displaystyle 2h^{2}=\cos {\frac {\pi }{n}}-\cos {\frac {2\pi }{n}}}$.

Volumul și aria anvelopei

Fie a lungimea laturii unei antiprisme uniforme. Atunci, volumul este

${\displaystyle V={\frac {n{\sqrt {4\cos ^{2}{\frac {\pi }{2n}}-1}}\sin {\frac {3\pi }{2n}}}{12\sin ^{2}{\frac {\pi }{n}}}}a^{3}}$

iar aria anvelopei este

${\displaystyle A={\frac {n}{2}}\left(\cot {\frac {\pi }{n}}+{\sqrt {3}}\right)a^{2}}$.

Poliedre înrudite

Există un set infinit de antiprisme trunchiate, inclusiv o formă de simetrie inferioară a octaedrului trunchiat (antiprismă triunghiulară trunchiată). Acestea pot fi alternate pentru a crea antiprisme snub, dintre care două sunt poliedre Johnson, iar antiprisma triunghiulară snub este o formă de simetrie inferioară a icosaedrului.

Antiprisme
				...
s{2,4}	s{2,6}	s{2,8}	s{2,10}	s{2,2n}
Antiprisme trunchiate
				...
ts{2,4}	ts{2,6}	ts{2,8}	ts{2,10}	ts{2,2n}
Antiprisme snub
J84	Icosaedru	J85	Fețe neregulate...
				...
ss{2,4}	ss{2,6}	ss{2,8}	ss{2,10}	ss{2,2n}

Simetrie

Grupul de simetrie al unei antiprisme drepte cu bază regulată și fețele laterale triunghiuri isoscele este D_nd de ordinul 4n, cu excepția cazului tetraedrului, care are grupul de simetrie mai mare T_d de ordinul 24, care are trei versiuni ale D_2d ca subgrupuri, și cazul octaedrului, care are grupul de simetrie mai mare O_h de ordinul 48, care are patru versiuni ale D_3d ca subgrupuri.

Grupul de simetrie admite simetria față de centru (inversiunea față de punctul din centru) dacă și numai dacă n este impar.

Grupul de rotații este D_n de ordinul 2n, cu excepția cazului tetraedrului, care are un grup de rotații mai mare T de ordinul 12, care are trei versiuni ale D ₂ ca subgrupuri, și cazul octaedrului, care are grupul de rotații mai mare O de ordinul 24, care are patru versiuni ale D_{3</ sub> ca subgrupuri.}

Antiprisme stelate

5/2-antiprismă			5/3-antiprismă
9/2-antiprismă		9/4-antiprismă		9/5-antiprismă

Antiprismele stelate uniforme sunt denumite după poligoanele stelate, {p/q}, de la bazle lor și există în versiuni directe sau retrograde. Formele retrograde, numite și retroprisme, au figurile vârfurilor intersectate și sunt notate cu fracții inversate, p/(p - q) în loc de p/q, de exemplu 5/3 în loc de 5/2.

În formele retrograde, dar nu și în formele directe, triunghiurile care unesc bazele stelate intersectează axa simetriei de rotație.

Unele antiprisme stelate retrograde cu baze poligonale convexe regulate nu pot fi construite cu muchii de lungimi egale, deci nu sunt poliedre uniforme.

Compușii de antiprisme stelate pot fi de asemenea construiți acolo unde p și q au factori comuni. De exemplu: o antiprismă stelată 10/4 este compusul a două antiprisme stelate 5/2.

Antiprisme stelate cu bazele având până la 12 laturi, după simetrii
Grup de simetrie sferică	Stelate uniforme				Alte stelate
D4d [2+,8] (2*5)					3.3/2.3.4
D5h [2,5] (*225)	3.3.3.5/2				3.3/2.3.5
D5d [2+,10] (2*5)	3.3.3.5/3
D6d [2+,12] (2*6)		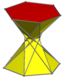			3.3/2.3.6
D7h [2,7] (*227)	3.3.3.7/2	3.3.3.7/4
D7d [2+,14] (2*7)	3.3.3.7/3
D8d [2+,16] (2*8)	3.3.3.8/3	3.3.3.8/5
D9h [2,9] (*229)	3.3.3.9/2	3.3.3.9/4
D9d [2+,18] (2*9)	3.3.3.9/5
D10d [2+,12] (2*10)	3.3.3.10/3
D11h [2,11] (*2.2.11)	3.3.3.11/2	3.3.3.11/4	3.3.3.11/6
D11d [2+,22] (2*11)	3.3.3.11/3	3.3.3.11/5	3.3.3.11/7
D12d [2+,24] (2*12)	3.3.3.12/5	3.3.3.12/7
...

Note

Bibliografie

• en Anthony Pugh (1976). Polyhedra: A visual approach. California: University of California Press Berkeley. ISBN 0-520-03056-7.  Chapter 2: Archimedean polyhedra, prisma and antiprisms

Vezi și

• Compus prismatic de antiprisme
• Compus prismatic de antiprisme cu libertate de rotație

Legături externe

• Materiale media legate de antiprismă la Wikimedia Commons
• en Eric W. Weisstein, Antiprism la MathWorld.
• en Nonconvex Prisms and Antiprisms
• en Paper models of prisms and antiprisms

Portal matematică

v • d • m Poliedru (categorie) 1–10 fețe Monoedru (1) · Diedru (2) · Triedru (3) · Tetraedru (4) · Pentaedru (5) · Hexaedru (6) · Heptaedru (7) · Octaedru (8) · Eneaedru (9) · Decaedru (10) 2–20 fețe Endecaedru (11) · Dodecaedru (12) · Tridecaedru (13) · Tetradecaedru (14) · Pentadecaedru (15) · Hexadecaedru (16) · Heptadecaedru (17) · Octadecaedru (18) · Eneadecaedru (19) · Icosaedru (20) >20 fețe Icositetraedru (24)  · Triacontaedru (30) · Icosidodecaedru (32) · Hexacontaedru (60) · Eneacontaedru (90) · Hectotriadioedru (132) · Apeiroedru (∞) (regulat) Noțiuni de bază față · latură · vârf · poliedru uniform (poliedru regulat · poliedru cvasiregulat · poliedru semiregulat) Poliedre convexe poliedru platonic · poliedru arhimedic · poliedru Catalan · poliedru Johnson Poliedre neconvexe poliedru Kepler–Poinsot · poliedru stelat (poliedru stelat uniform) · hemipoliedru Poliedre prismatice prismă · antiprismă · trunchi · cupolă · pană · piramidă · paralelipiped