Hauteur d'un triangle

Pour les articles homonymes, voir Hauteur.

{\displaystyle H_{A}} — Deux triangles ABC avec leur hauteur issue de A et le pied $H_{A}$ de la hauteur.

En géométrie plane, une hauteur d'un triangle est une droite passant par un sommet et coupant perpendiculairement le côté opposé à ce sommet (éventuellement prolongé). Les pieds des hauteurs sont les projetés orthogonaux de chacun des sommets sur la droite portant le côté opposé.

On donne également le nom de hauteur au segment joignant un sommet et le pied de la hauteur passant par ce sommet, ainsi qu'à la longueur de ce segment, soit la distance séparant un sommet et la droite portant son côté opposé^[1].

Pour une hauteur passant par un sommet donné (appelé apex), la base associée à cette hauteur est le côté opposé au sommet (ou sa longueur).

Calcul des hauteurs

Avec les notations classiques d'un triangle (ABC) , la hauteur (en tant que distance) issue de A vaut ${\textstyle h_{A}=2{S \over a}}$ où $S$ est l'aire du triangle (laquelle s'exprime en fonction des côtés par la formule de Héron). Les hauteurs sont donc inversement proportionnelles aux longueurs des côtés auxquelles elles aboutissent.

Orthocentre

Les trois hauteurs d'un triangle sont concourantes. Leur point d'intersection $H$ , est nommé orthocentre du triangle. L'orthocentre d'un triangle acutangle est situé à l'intérieur du triangle tandis que celui d'un triangle obtusangle est situé à l'extérieur.

Une démonstration utilise la relation ${\overrightarrow {AH}}\cdot {\overrightarrow {BC}}+{\overrightarrow {BH}}\cdot {\overrightarrow {CA}}+{\overrightarrow {CH}}\cdot {\overrightarrow {AB}}=0$ qui montre que si un point $H$ appartient à deux hauteurs, il appartient aussi à la troisième.

Démonstration par homothétie

On considère l'homothétie de centre le centre de gravité du triangle et de rapport –2. Elle transforme le triangle ABC en un triangle A'B'C' (triangle antimédian du triangle ABC).

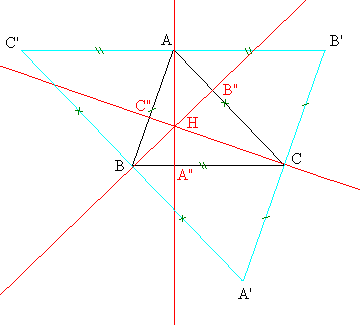
Le point I milieu de [BC] (non représenté dans la figure précédente) a pour image le point A qui est donc le milieu de [B'C']. La hauteur issue de A est perpendiculaire à [BC] donc à [B'C']. Comme elle passe de plus par son milieu, c'est la médiatrice du segment [B'C'].

On démontre ainsi que les trois hauteurs du triangle ABC sont les trois médiatrices du triangle A'B'C'^[2]. Par conséquent, elles sont concourantes.


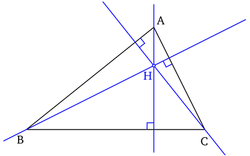Hauteurs et orthocentre d'un triangle acutangle.		Hauteurs et orthocentre d'un triangle obtusangle.

L'orthocentre est le barycentre des systèmes :

{\begin{pmatrix}A&B&C\\\tan {\widehat {A}}&\tan {\widehat {B}}&\tan {\widehat {C}}\end{pmatrix}}

{\begin{pmatrix}A&B&C\\a/\cos {\widehat {A}}&b/\cos {\widehat {B}}&c/\cos {\widehat {C}}\end{pmatrix}}

ou encore

{\begin{pmatrix}A&B&C\\{\frac {1}{b^{2}+c^{2}-a^{2}}}&{\frac {1}{c^{2}+a^{2}-b^{2}}}&{\frac {1}{a^{2}+b^{2}-c^{2}}}\end{pmatrix}}

Ses coordonnées trilinéaires par rapport aux côtés du triangle sont :

1/\cos {\widehat {A}}:1/\cos {\widehat {B}}:1/\cos {\widehat {C}}

\cos {\widehat {A}}-\sin {\widehat {B}}\sin {\widehat {C}}:\cos {\widehat {B}}-\sin {\widehat {C}}\sin {\widehat {A}}:\cos {\widehat {C}}-\sin {\widehat {A}}\sin {\widehat {B}}

Pour un triangle acutangle, notant R le rayon du cercle circonscrit :

Les distances aux sommets sont données par : $AH=a\cot {\widehat {A}}=2R\cos {\widehat {A}}$ et les formules permutées.

On en déduit la relation : $a.BH.CH+b.CH.AH+c.AH.BH=abc$ ^[3].

Les distances aux côtés sont données par : $HH_{A}={\frac {H_{A}B.H_{A}C}{h_{A}}}={\frac {abc}{2S}}\cos {\widehat {B}}\cos {\widehat {C}}=2R\cos {\widehat {B}}\cos {\widehat {C}}$ .

Les trois sommets du triangle et leur orthocentre forment un quadrangle orthocentrique : chacun de ces points est l'orthocentre du triangle formé par les trois autres points.

Dans un triangle, le centre du cercle inscrit dans le triangle et les centres des cercles exinscrits forment également un quadrangle orthocentrique.

Triangle orthique

Article détaillé : Triangle orthique.

Les pieds des hauteurs forment un triangle, à la fois triangle cévien et triangle podaire de l'orthocentre, appelé le triangle orthique du triangle.

Les hauteurs sont les bissectrices de ce triangle^[4].

Symétriques de l'orthocentre

Les symétriques A₁, B₁ et C₁ de l'orthocentre H par rapport aux milieux des côtés du triangle se trouvent sur le cercle circonscrit.

Les symétriques orthogonaux A₂, B₂ et C₂ de l'orthocentre par rapport aux côtés du triangle (ou par rapport aux pieds des hauteurs) se trouvent également sur le cercle circonscrit.

Ceci découle de l'observation que d'une part ${\widehat {AHC}}={\widehat {A}}+{\widehat {C}}$ , et que d'autre part ${\widehat {AB_{1}C}}={\widehat {AHC}}=\pi -{\widehat {B}}$ , et de même pour $B_{2}$ .

Pour une autre démonstration utilisant des homothéties voir Cercle d'Euler.

Cercle de Taylor

Soit A', B' et C' les pieds des hauteurs du triangle. On note A₂ et A₃ les projetés orthogonaux de A' sur les côtés AB et AC du triangle et on définit de même B₂ et B₃ par rapport à B' et C₂ et C₃ par rapport à C'. Les six points ainsi définis sont cocycliques : ils sont situés sur le cercle de Taylor du triangle ^[5]^,^[4] .

On a : (A₂A₃, BC) = (AB, AC), la droite (A₂A₃) est antiparallèle de (BC) par rapport à (AB) et (AC), et des propriétés analogues pour (B₂B₃) et (C₂C₃).

(B₂C₂) est parallèle à (BC). De même (A₂C₃) //(AC) et (A₃B₃)//(AB).

C'est la configuration d'un cercle de Tucker particulier, dit cercle de Taylor.

On trouve A₂A₃ = B₂B₃ = C₂C₃.

L'hexagone ayant pour sommets ces six projections est l'hexagone de Catalan.

Centre du cercle de Taylor

Les trois droites (A₁A₂), (B₁B₂) et (C₁C₂) joignant les projections sont parallèles aux côtés du triangle orthique et coupent ses côtés en leurs milieux P, Q et R. Ces droites déterminent les côtés du triangle PQR qui est le triangle médian du triangle orthique.

Le centre est sur la droite reliant le centre O du cercle circonscrit au point de Lemoine, passant par les points X15 , X32 au milieu de O-X52

Si le triangle ABC est acutangle alors le centre du cercle de Taylor est le centre du cercle inscrit dans le triangle médian du triangle orthique.

Centre du cercle de Taylor d'un triangle acutangle.

Si le triangle ABC est obtusangle alors le centre du cercle de Taylor est un des centres des cercles exinscrits du triangle PQR. Plus précisément, si ABC est obtus en A (respectivement en B, en C), alors le centre du cercle de Taylor est le centre du cercle exinscrit à PQR dans l'angle de sommet P, milieu de [B’C’] (respectivement Q milieu de [C’A’] , R milieu de [A’B’]).

Centre du cercle de Taylor d'un triangle obtus en C.

Axe orthique

Article détaillé : Axe orthique.

Dans un triangle ABC, soit A' (respectivement B' et C') le pied de la hauteur issue de A (respectivement issue de B et de C).

A₁, B₁ et C₁ sont les trois autres points d'intersection des côtés du triangle ABC et de ceux du triangle orthique A’B’C’ : on note A₁ l'intersection de (BC) et de (B'C'), B₁ l'intersection de (AC) et de (A'C'), C₁ l'intersection de (AB) et de (A'B').

Les trois points A₁, B₁ et C₁ sont alignés sur une droite dénommée l'axe orthique du triangle.

L'axe orthique est aussi l'axe radical du cercle circonscrit et du cercle d'Euler.

La droite d'Euler, ligne des centres des deux cercles, est perpendiculaire à l'axe.

Cercle des hauteurs

Notant $H_{A},H_{B},H_{C}$ les pieds des hauteurs issues de $A,B,C$ , les expressions ci-dessus montrent qu'on a les égalités, avec $R$ le rayon du cercle circonscrit :

k^{2}=HA\times HH_{A}=HB\times HH_{B}=HC\times HH_{C}={\frac {HA\cdot HB\cdot HC}{2R}}

Le cercle de centre $H$ et de rayon $k$ est appelé cercle des hauteurs ou cercle de Mention, du nom de Jules-Alexandre Mention, qui l'a étudié.

Cercle de Mention dans le cas où l'orthocentre est à l'intérieur du triangle

Dans le cas où le triangle est obtusangle, Mention a établi que ce cercle était le lieu des centres des hyperboles équilatères inscrites au triangle, c'est-à-dire tangentes aux côtés du triangle^[6].Toujours dans ce cas, on peut voir que (BC) est la polaire de A par rapport à ce cercle, et, de même, que (CA) est la polaire de B et (AB) celle de C, d'où l'autre nom de cercle polaire^[7]. Dans ce cas, le cercle des hauteurs, le cercle circonscrit et le cercle d'Euler ont deux points communs^[7].

Cercle de Mention dans le cas où l'orthocentre est à l'extérieur du triangle

Notes et références

↑ Alexander Andre Victor Sarrazin de Montferrier, Dictionnaire de mathématiques pures et appliquées, 1838 (lire en ligne), p. 574.
↑ Trajan Lalesco, La géométrie du triangle, Jacques Gabay, 1987 (ISBN 2-87647-007-1), p. 2
↑ Mohammed AASSILA, 1000 challenges mathématiques, Géométrie, Ellipses, 2018, p. 124 et 132
↑ ^{a et b} Patrice Debart, « Triangle orthique », sur debart.fr
↑ Yvonne et René Sortais, Géométrie de l'espace et du plan, Hermann, 1988, p. 105-106
↑ J. Mention, « Sur l'hyperbole équilatère », Nouvelles annales de mathématiques : journal des candidats aux écoles polytechnique et normale, vol. 2, n^o 4,‎ 1865, p. 30-39 (lire en ligne)
↑ ^{a et b} Serge Mehl, « Cercle polaire d'un triangle également appelé cercle conjugué », sur ChronoMath, une chronologie des MATHÉMATIQUES (consulté le 19 avril 20234)

Voir aussi

Bibliographie

Jacques Bouteloup, « Cercles de Tücker », Quadrature,‎ janvier-mars 2007 (lire en ligne).
Jean-Denis Eiden, Géométrie analytique classique, Calvage & Mounet, 2009 (ISBN 978-2-91-635208-4).
Jean Fresnel, Méthodes modernes en géométrie
Bruno Ingrao, Coniques affines, euclidiennes et projectives, C&M (ISBN 978-2-916352-12-1)

Articles connexes

Théorème de Hamilton

v · m Triangles
Description	Sommet Apex Côté Angle Base
Types	Triangle équilatéral Triangle isocèle Triangle d'or Triangle rectangle Angle droit Cathète Hypoténuse Triangle de Kepler Triangle obtusangle Triangle acutangle Triangle isocèle rectangle Triangle pseudo-rectangle Triangle scalène Triangle de Héron
Points remarquables (Nombre de Kimberling)	Centres : Centre du cercle inscrit Centre de gravité Centre du cercle circonscrit Orthocentre Centre du cercle d'Euler Centre du cercle de Spieker Points de Brocard Points de Feuerbach Point de Fermat ou Point de Torricelli Point de Longchamps Point de Miquel Point de Gergonne Point de Nagel Point de Vecten Points isogonaux Points isodynamiques Point de Lemoine Points de Terquem Points de Napoléon Mittenpunkt
Droites remarquables	Cévienne Hauteur Médiane Bissectrice Médiatrice Droite de Brocard Droite d'Euler Droite de Lemoine Droite de Newton Droite de Simson (ou droite de Wallace) Droite de Steiner Ménélienne Symédiane Axe orthique Droite centrale
Cercles remarquables	Cercle circonscrit Cercle exinscrit Cercle inscrit Cercle d'Euler Cercle d'Apollonius Cercles de Lemoine Cercle de Longchamps Cercle de Miquel Cercle de Taylor Cercle de Tucker Cercle podaire Cercle de Brocard Cercle de Spieker Cercle de Fuhrmann Cercles de Johnson Cercle pédal
Triangles remarquables	Triangle de Bevan Triangle de Feuerbach Triangle de Gergonne Triangle de Morley Triangle de Nagel Triangle inscrit de périmètre minimal (Problème de Fagnano) Triangle médian Triangle orthique Triangle podaire Triangle tangentiel Triangle de Fuhrmann
Courbes remarquables	Deltoïde de Steiner Coniques Conique inscrite de Serret (ou de MacBeath) Conique orthique Hyperbole de Kiepert Paraboles Parabole tritangente Parabole de Kiepert Ellipses Ellipse de Mandart Ellipse de Steiner Coniques circonscrites et inscrites à un triangle Cubiques
Théorèmes	Théorème de Pythagore Théorème de Thalès Théorème de Napoléon Théorème japonais de Carnot Théorème de Ménélaüs Théorème de Morley Théorème de Nagel Théorème de Neuberg Théorème de Hamilton Théorème d'Euler Théorème de Feuerbach Théorème de Viviani Avec des céviennes Théorème de Ceva Théorème de Gergonne Théorème de Stewart Théorème de Terquem Théorème de Routh Théorème de Jacobi Avec des cercles Théorème des six cercles Théorème des trois cercles de Miquel
Relations entre triangles	Triangles isométriques Triangles semblables Inégalités dans le triangle
Résolution	Loi des cosinus Loi des sinus Loi des tangentes Loi des cotangentes Aire Formule de Héron