Limite superiore e limite inferiore

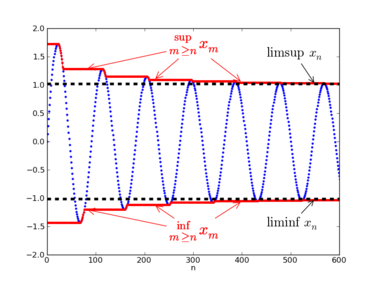
In matematica vengono presi in considerazione due tipi di costruzioni, chiamate rispettivamente limite inferiore (o anche minimo limite) e limite superiore (o anche massimo limite) che rispetto a quella di limite sono più deboli ma di attuazione più generale e che possono essere utili per trattare varie questioni sui limiti. Le due nozioni si introducono per funzioni a valori reali, per successioni di insiemi e, in generale, per funzioni aventi come codominio un insieme parzialmente ordinato. Nel caso più semplice di una successione di numeri reali queste due nozioni servono a "limitare" il codominio di questa funzione, cioè la regione nella quale si trovano "definitivamente" i componenti della successione.

Limite inferiore e superiore di una successione

Data una successione di numeri reali ${\displaystyle ({x_{n}})}$, siano:

${\displaystyle {b_{k}}=\sup\{x_{k},x_{k+1},\dots \}\quad k=1,2,\dots }$

${\displaystyle \beta =\inf\{b_{1},b_{2},\dots \}}$

Allora ${\displaystyle \beta }$ è il limite superiore di ${\displaystyle ({x_{n}})}$:^[1]

${\displaystyle \beta =\limsup _{n\rightarrow \infty }x_{n}:=\lim _{n\to \infty }{\Big (}\sup _{m\geq n}x_{m}{\Big )}=\inf\{\,\sup\{\,x_{k}:k\geq n\,\}:n\geq 0\,\}}$

Si nota che:

${\displaystyle \lim _{k\to \infty }b_{k}=\beta }$

ed esiste una sottosuccessione ${\displaystyle {x_{n_{i}}}}$di ${\displaystyle {x_{n}}}$ tale che:

${\displaystyle \lim _{i\to \infty }x_{n_{i}}=\beta }$

e ${\displaystyle \beta }$ è il più grande numero che gode di tale proprietà.

In modo analogo si definisce il limite inferiore di una successione:^[2]

${\displaystyle \liminf _{n\to \infty }x_{n}:=\lim _{n\to \infty }{\Big (}\inf _{m\geq n}x_{m}{\Big )}=\sup\{\,\inf\{\,x_{m}:m\geq n\,\}:n\geq 0\,\}}$

Talvolta per indicare i limiti superiore e inferiore si usa la notazione:

${\displaystyle \varliminf _{n\to \infty }x_{n}:=\liminf _{n\to \infty }x_{n}\quad \varlimsup _{n\to \infty }x_{n}:=\limsup _{n\to \infty }x_{n}}$

Se gli elementi della successione appartengono ad un insieme parzialmente ordinato del quale esistano gli estremi superiore e inferiore, i limiti superiore e inferiore esistono sempre, e si ha:

${\displaystyle -\limsup _{n\rightarrow \infty }(-x_{n})=\liminf _{n\to \infty }x_{n}}$

Se la successione ${\displaystyle {x_{n}}}$ converge si ha:^[2]

${\displaystyle \limsup _{n\to \infty }(x_{n})=\liminf _{n\to \infty }(x_{n})=\lim _{n\to \infty }x_{n}}$

Le nozioni di limite inferiore e superiore sono collegate alla O-grande, in quanto tali entità forniscono delle restrizioni ai valori della successione soltanto al limite. In alternativa, avendo introdotto i concetti di valore limite e classe limite, i limiti superiore e inferiore di una successione possono essere definiti semplicemente come il massimo ed il minimo della classe limite di tale successione, che si dimostra esistere sempre.

Limiti inferiore e superiore di una funzione reale

Sia ${\displaystyle f:A\rightarrow \mathbb {R} }$ una funzione definita in un sottoinsieme ${\displaystyle A}$ di un qualsiasi spazio topologico, sia ${\displaystyle x_{0}}$ un punto di accumulazione e ${\displaystyle I(x_{0})}$ la famiglia di intorni di ${\displaystyle x_{0}}$ in ${\displaystyle A}$, con ${\displaystyle U\in I(x_{0})}$. Il limite inferiore di una funzione reale per ${\displaystyle x\rightarrow x_{0}}$ viene definito come:

${\displaystyle \liminf _{x\to x_{0}}f(x)=\sup _{U}\,\left[\inf _{x\in (U\cap A\setminus \{x_{0}\})}f(x)\right]=\sup\{\,\inf\{f(x)|\;x\in (U\cap A\setminus \{x_{0}\})\,\}\,\}}$

Intuitivamente, il limite inferiore di ${\displaystyle f}$ per ${\displaystyle x}$ → ${\displaystyle x_{0}}$ è il valore massimo, al variare dell'intorno di ${\displaystyle x_{0}}$, del più piccolo valore che la funzione assume in un singolo intorno.

Il limite superiore di una funzione reale per ${\displaystyle x\rightarrow x_{0}}$ viene definito analogamente:

${\displaystyle \limsup _{x\to x_{0}}f(x)=\inf _{U}\,\left[\sup _{x\in (U\cap A\setminus \{x_{0}\})}f(x)\right]=\inf\{\,\sup\{f(x)|x\in (U\cap A\setminus \{x_{0}\})\,\}\,\}}$

Esso corrisponde dunque al valore più piccolo tra i valori massimi che la funzione assume in ogni intorno del punto.

Caratteristiche e proprietà

Sfruttando le definizioni degli algoritmi di estremo superiore e inferiore, valgono queste caratteristiche dei due limiti, cioè

${\displaystyle \liminf _{x\to x_{0}}f(x)=m\in \mathbb {R} \iff \left\{{\begin{matrix}\forall \varepsilon \!>\!0\;\exists \,U_{\varepsilon }(x_{0})|\;\forall x\in (U_{\varepsilon }\!\cap \!A\!\setminus \!\{x_{0}\})\implies f(x)>m-\varepsilon \\\!\!\!\!\!\!\!\!\!\!\!\!\!\forall \varepsilon \!>\!0\;\forall \,U_{\varepsilon }(x_{0}),\exists x\in (U_{\varepsilon }\!\cap \!A\!\setminus \!\{x_{0}\})|\;f(x)<m+\varepsilon \end{matrix}}\right.}$

La prima riga afferma che definitivamente ogni livello più basso di ${\displaystyle m}$ è invalicabile, cioè tutto un intorno di ${\displaystyle x_{0}}$ ha immagini maggiori di ${\displaystyle m-\varepsilon }$ (corrispondente alla proprietà di essere un estremo superiore); la seconda che in ogni intorno si può trovare una ${\displaystyle x}$ con immagine arbitrariamente vicina a ${\displaystyle m}$ (dovuta all'essere un estremo inferiore).

Nel caso infinito, valgono invece queste proprietà:

${\displaystyle \liminf _{x\to x_{0}}f(x)=-\infty \iff \forall K\!>\!0\;\forall \,U(x_{0}),\exists x\in (U\!\cap \!A\!\setminus \!\{x_{0}\})|\;f(x)<-K}$

${\displaystyle \liminf _{x\to x_{0}}f(x)=+\infty \iff \forall K\!>\!0\;\exists \,U(x_{0}),\forall x\in (U\!\cap \!A\!\setminus \!\{x_{0}\})|\;f(x)>K}$

Le proprietà per il massimo limite si ricavano analogamente.

Inoltre, al contrario del limite, limite inferiore e superiore esistono sempre, in quanto calcolate con algoritmi di estremo superiore e estremo inferiore su insiemi reali. Vale inoltre che:

${\displaystyle \liminf _{x\rightarrow x_{0}}f(x)\leq \limsup _{x\rightarrow x_{0}}f(x)}$

e l'uguaglianza sussiste se e solo se esiste in ${\displaystyle \mathbb {R} \cup \{-\infty ,+\infty \}}$ il limite ${\displaystyle \lim _{x\rightarrow x_{0}}f(x)}$, che sarà uguale al valore comune di ${\displaystyle \liminf }$ e ${\displaystyle \limsup }$.

Convergenza delle successioni di numeri reali

Si osserva che le definizioni precedenti hanno senso in ogni insieme parzialmente ordinato nel quale esistano gli estremi superiori e inferiori. Questo induce a estendere le definizioni a successioni aventi i componenti in ambienti più "esotici" dell'insieme dei numeri reali. In ogni reticolo completo esistono i sup e gli inf di qualsiasi sottoinsieme: quindi risulta particolarmente interessante considerare i limiti inferiore e superiore delle sequenze di elementi di reticoli completi.

Si osserva anche che l'insieme dei numeri reali ${\displaystyle \mathbb {R} }$ non costituisce un reticolo completo, ma che si ottiene la sua completezza aggiungendogli l'infinito negativo e il positivo: in effetti l'insieme ${\displaystyle [-\infty ,\infty ]}$ costituisce un insieme totalmente ordinato completo.

In questo ambiente una successione ${\displaystyle \{x_{n}:n\in \mathbb {N} \}}$ converge se e solo se ${\displaystyle \liminf x_{n}=\limsup x_{n}}$, e in tale caso ${\displaystyle \lim x_{n}}$ è uguale al loro comune valore (si osserva che quando si opera nel solo ${\displaystyle \mathbb {R} }$, non si prende in considerazione la divergenza a ${\displaystyle -\infty }$ o a ${\displaystyle +\infty }$).

Come esempio si consideri la sequenza data da ${\displaystyle x_{n}=\sin n}$. In virtù del fatto che pi greco è un numero irrazionale, si dimostra che ${\displaystyle \liminf x_{n}=-1}$ e ${\displaystyle \limsup x_{n}=+1}$.

Se ${\displaystyle I\equiv \liminf x_{n}}$ e ${\displaystyle S\equiv \limsup x_{n}}$, allora l'intervallo ${\displaystyle [I,S]}$ potrebbe non contenere nessuno dei numeri ${\displaystyle x_{n}}$, ma ogni ampliamento anche molto piccolo ma fissato ${\displaystyle [I-\epsilon ,S+\epsilon ]}$ (dipendente da un ${\displaystyle \epsilon >0}$ "arbitrariamente piccolo") contiene gli ${\displaystyle x_{n}}$, al più ad eccezione di un insieme finito di indici n. In effetti l'intervallo ${\displaystyle [I,S]}$ è il più piccolo intervallo chiuso con questa proprietà.

Un esempio tratto dalla teoria dei numeri riguarda:

${\displaystyle \liminf _{n}(p_{n+1}-p_{n})}$

dove con ${\displaystyle p_{n}}$ si denota l'n-esimo numero primo. Il valore di questo limite inferiore si è congetturato essere 2: questa è la congettura dei numeri primi gemelli, tuttora indimostrata; il risultato più avanzato (ottenuto tra il 2013^[3] e il 2014^[4]) è che tale limite sia minore o uguale a 246.

Successioni di insiemi

L'insieme delle parti ${\displaystyle P(X)}$ di un insieme ${\displaystyle X}$ costituisce un reticolo completo e talora risulta utile prendere in considerazione i limiti superiore e inferiore di successioni in ${\displaystyle P(X)}$, cioè successioni di sottoinsiemi di ${\displaystyle X}$. Se ${\displaystyle X_{n}}$ è una tale successione, allora un elemento ${\displaystyle a}$ di ${\displaystyle X}$ appartiene a ${\displaystyle \liminf X_{n}}$ se e solo se esiste un intero naturale ${\displaystyle n_{0}}$ tale che ${\displaystyle a}$ appartiene ad ${\displaystyle X_{n}}$ per tutti gli ${\displaystyle n>n_{0}}$. L'elemento ${\displaystyle a}$ appartiene a ${\displaystyle \limsup X_{n}}$ se e solo se per ogni intero naturale ${\displaystyle n_{0}}$ esiste un indice ${\displaystyle n>n_{0}}$ tale che ${\displaystyle a}$ appartiene a ${\displaystyle X_{n}}$. In altre parole,${\displaystyle \limsup X_{n}}$ consiste di quegli elementi che si trovano in insiemi della forma ${\displaystyle X_{n}}$ per una infinità di n, mentre ${\displaystyle \liminf X_{n}}$ consiste di quegli elementi che sono esclusi al più da un numero finito di ${\displaystyle X_{n}}$.

Usando le notazioni usuali della teoria degli insiemi, l'infimo di una successione di insiemi è l'intersezione numerabile degli insiemi, cioè il più esteso insieme incluso in tutti gli insiemi da intersecare:

${\displaystyle \inf \left\{\,X_{n}:n=1,2,3,\dots \,\right\}={\bigcap _{n=1}^{\infty }}X_{n}}$

La successione ${\displaystyle \{I_{n}:n\in \mathbb {N} \}}$, dove con ${\displaystyle I_{n}}$ si denota l'infimo degli insiemi con indice maggiore o uguale a n, è non decrescente, in quanto ${\displaystyle I_{n}\subset I_{n+1}}$. Quindi l'unione degli infimi relativi agli indici da 1 a n è uguale all'n-esimo infimo. Facendo andare questa successione di insiemi al limite:

${\displaystyle \liminf _{n\rightarrow \infty }X_{n}={\bigcup _{n=1}^{\infty }}\left({\bigcap _{m=n}^{\infty }}X_{m}\right)}$

Il limsup può essere definito simmetricamente. Il supremo di una successione di insiemi è il più piccolo insieme che contiene tutti gli insiemi, cioè l'unione numerabile degli insiemi.

${\displaystyle \sup \left\{\,X_{n}:n=1,2,3,\dots \,\right\}={\bigcup _{n=1}^{\infty }}X_{n}}$

Il limsup è invece la intersezione numerabile di questa successione non crescente (ogni supremo è un sottoinsieme del supremo che lo precede)

${\displaystyle \limsup _{n\rightarrow \infty }X_{n}={\bigcap _{n=1}^{\infty }}\left({\bigcup _{m=n}^{\infty }}X_{m}\right)}$

Per un esempio vedi lemma di Borel-Cantelli. Quando questi due insiemi coincidono si parla di insieme limite della successione ${\displaystyle (X_{n})_{n}}$.

Note

Bibliografia

• Walter Rudin, Real and Complex Analysis, Mladinska Knjiga, McGraw-Hill, 1970, ISBN 0-07-054234-1.
• (EN) H. Amann, Escher, Joachim, Analysis, Basel; Boston: Birkhäuser, 2005, ISBN 0-8176-7153-6.
• (EN) Mario O González, Classical complex analysis, New York: M. Dekker, 1991, ISBN 0-8247-8415-4.

Voci correlate

• Classe limite
• Estremo superiore e estremo inferiore
• Funzione semicontinua
• Limite (matematica)
• Successione (matematica)

Altri progetti

• Wikiversità contiene risorse sui limiti
• Wikimedia Commons contiene immagini o altri file sui limiti