偏相関
偏相関(へんそうかん、英: partial correlation)は、別の交絡因子による影響を取り除いた関心のある2つの変数の間の相関を表す概念である。ピアソンの積率相関係数を使用すると、別の交絡因子がある場合に誤解を招く結果が得られる。この誤解を招く情報は、偏相関係数を計算し交絡変数を制御することによって回避できる。
偏相関係数は、ピアソンの積率相関係数と同様に、–1から1の範囲の値を取る。偏相関係数の値が–1のときは、別の交絡因子による影響を取り除いた完全な負の相関(線形関係)を表す。偏相関係数の値が1のときは完全な正の相関(線形関係)を表し、値が0のときは線形関係がないことを表す。
定義
n 個の制御変数 Z = {Z1, Z2, ..., Zn} が与えられた場合の X と Y の間の偏相関 ρXY·Z は、eX(X を Z で線形回帰したときの残差)と eY(Y を Z で線形回帰したときの残差)の相関である。
計算
関連する2つの線形回帰問題を解き、残差を取得し、残差間の相関を計算する。
線形回帰の使用
例
| X | Y | Z |
|---|---|---|
| 2 | 1 | 0 |
| 4 | 2 | 0 |
| 15 | 3 | 1 |
| 20 | 4 | 1 |
> X = c(2,4,15,20) > Y = c(1,2,3,4) > Z = c(0,0,1,1) > mm1 = lm(X~Z) > res1 = mm1$residuals > mm2 = lm(Y~Z) > res2 = mm2$residuals > cor(res1,res2) [1] 0.919145 > cor(X,Y) [1] 0.9695016 > generalCorr::parcorMany(cbind(X,Y,Z)) nami namj partij partji rijMrji [1,] "X" "Y" "0.8844" "1" "-0.1156" [2,] "X" "Z" "0.1581" "1" "-0.8419"
再帰式の使用
逆行列の使用
解釈
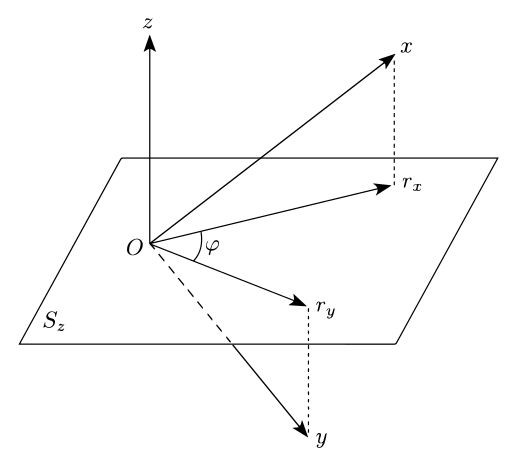
幾何学的
条件付き独立性テストとして
参照:フィッシャー変換
半偏相関(部分相関)
時系列分析で使用
関連項目
参考文献
外部リンク

ウィキバーシティに偏相関に関する学習教材があります。
- Prokhorov, A.V. (2001), “Partial correlation coefficient”, in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4, https://www.encyclopediaofmath.org/index.php?title=Partial_correlation_coefficient&oldid=14288
- Mathematical formulae in the "Description" section of the IMSL Numerical Library PCORR routine
- A three-variable example
| |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 標本調査 | |||||||||||||||
| 記述統計学 |
| ||||||||||||||
| 推計統計学 |
| ||||||||||||||
| ベイズ統計学 |
| ||||||||||||||
| 相関 |
| ||||||||||||||
| モデル | |||||||||||||||
| 回帰 |
| ||||||||||||||
| 分類 |
| ||||||||||||||
| 教師なし学習 |
| ||||||||||||||
| 統計図表 | |||||||||||||||
| 生存時間分析 | |||||||||||||||
| 歴史 |
| ||||||||||||||
| 応用 | |||||||||||||||
| 出版物 |
| ||||||||||||||
| 全般 | |||||||||||||||
| その他 | |||||||||||||||
| | |||||||||||||||











