Distribució khi quadrat

${\displaystyle \chi ^{2}}$

Funció de densitat de probabilitat
Funció de distribució de probabilitat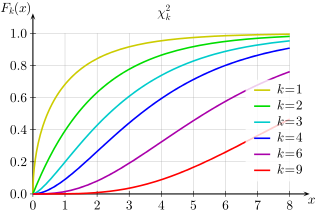
Tipus	família exponencial, Distribució khi quadrat no central, distribució gamma, Generalized chi-squared distribution (en) i distribució de probabilitat contínua
Notació	${\displaystyle \chi ^{2}(k)\;}$ o ${\displaystyle \chi _{k}^{2}\!}$
Paràmetres	${\displaystyle k\in (0,\infty )}$ (graus de llibertat)
Suport	${\displaystyle x>0}$
fdp	${\displaystyle {\frac {1}{2^{k/2}\Gamma (k/2)}}\;x^{k/2-1}e^{-x/2}\,\ x>0}$
FD	${\displaystyle {\frac {1}{\Gamma (k/2)}}\;\gamma \left({\frac {k}{2}},\,{\frac {x}{2}}\right)\;}$
Esperança matemàtica	${\displaystyle k}$
Mediana	${\displaystyle \approx k{\bigg (}1-{\frac {2}{9k}}{\bigg )}^{3}\;}$
Moda	${\displaystyle k-2,\ {\text{si}}\ k\geq 2}$
Variància	${\displaystyle 2k\;}$
Coeficient de simetria	${\displaystyle {\sqrt {8/k}}\,}$
Curtosi	${\displaystyle {\frac {12}{\nu }}}$
Entropia	${\displaystyle {\frac {k}{2}}+\ln(2\Gamma ({\frac {k}{2}}))+(1-{\frac {k}{2}})\psi ({\frac {k}{2}})}$
FGM	${\displaystyle (1-2t)^{-\nu /2},\ t\in (-\infty ,1/2)}$
FC	${\displaystyle (1-2\mathrm {i} t)^{-\nu /2}}$
Mathworld	Chi-SquaredDistribution

En Teoria de la probabilitat i Estadística la distribució distribució khi quadrat ${\displaystyle \chi ^{2}}$(pronunciat [xi] o [ci]), també anomenada khi quadrat de Pearson, amb ${\displaystyle k}$ de llibertat és la distribució de la suma dels quadrats de ${\displaystyle k}$ variables aleatòries normals estàndard independents. És un cas particular de la distribució gamma i es pot estendre a un nombre no enter de graus de llibertat. És molt important en Estadística ja que intervé en nombrosos tests estadístics, com el de la ${\displaystyle t}$ de Student o de la ${\displaystyle \chi ^{2}}$ de Pearson, així com en la construcció de diversos intervals de confiança.

La referència bàsica d'aquest article és Johnson et al.^[1].

Definició, funció de densitat i funció de distribució

Siguin ${\displaystyle Z_{1},\dots ,Z_{k}}$ variables aleatòries independents, totes amb distribució normal estàndard ${\displaystyle {\mathcal {N}}(0,1)}$. La variable aleatòria

es diu que té una distribució ${\displaystyle \chi ^{2}}$ amb ${\displaystyle k}$ graus de llibertat i s'escriu ${\displaystyle Q\sim \chi _{k}^{2}}$ o ${\displaystyle Q\sim \chi ^{2}(k)}$ .

La funció de densitat és

on ${\displaystyle \Gamma (a)}$ és la funció gamma. Per tant, tenim que la distribució coincideix amb una distribució gamma amb paràmetre de forma ${\displaystyle k/2}$ i paràmetre d'escala 2, ${\displaystyle Q\sim \Gamma {\Big (}{\frac {k}{2}},2{\Big )}}$ .

Funció de distribució

La funció de distribució es pot escriure en termes de la funció gamma incompleta:

on ${\displaystyle \gamma (\nu ,x)}$ és la funció gamma incompleta inferior.

Extensió a graus de llibertat no enters

La funció ${\displaystyle f(x;k)}$ està ben definida i és una funció de densitat per a qualsevol ${\displaystyle k\in (0,\infty )}$: en efecte, fixat qualsevol nombre real ${\displaystyle k>0}$, tenim que ${\displaystyle f(x;k)\geq 0}$ i ${\displaystyle \int _{-\infty }^{\infty }f(x;k)\,dx=1}$. Aleshores, una variable aleatòria amb aquesta densitat es diu que té una distribució ${\displaystyle \chi ^{2}}$ amb ${\displaystyle k}$ graus de llibertat. Alternativament, la distribució ${\displaystyle \Gamma {\Big (}{\frac {k}{2}},2{\Big )}}$ està definida per a qualsevol ${\displaystyle k\in (0,\infty )}$. A partir d'ara, suposarem que ${\displaystyle k\in (0,\infty )}$. i especificarem quan suposem que ${\displaystyle k}$ és un nombre natural.

Moments, funció generatriu de moments i funció característica

Moments

Aquestes propietats es dedueixen particularitzant les corresponents propietats de la distribució gamma. Si ${\displaystyle Q\sim \chi ^{2}(k)}$ aleshores té moments de tots els ordres, que valen

Utilitzant la funció Gamma es pot escriure

$${\displaystyle E[Q^{n}]=2^{n}\,{\frac {\Gamma {\big (}(k/2)+n{\big )}}{\Gamma (k/2)}}.}$$

En particular,

d'on Així,

$${\displaystyle E[Q]=k\quad {\text{i}}\quad {\text{Var}}(Q)=2k.}$$

Moments d'ordre negatiu

Si ${\displaystyle X}$ és una variable aleatòria positiva, ${\displaystyle X\geq 0}$, aleshores per a qualsevol ${\displaystyle r>0}$ podem calcular

però pot donar ${\displaystyle +\infty }$ . Quan dóna finit, llavors es diu que la variable ${\displaystyle X}$ té moment d'ordre negatiu ${\displaystyle -r}$.^[2]

Sigui ${\displaystyle Q\sim \chi ^{2}(k)}$. Llavors, si ${\displaystyle r\in (0,\nu /2)}$ , ${\displaystyle Q}$ té moment d'ordre negatiu ${\displaystyle -r}$ i val ^[2]

Per exemple, si ${\displaystyle \nu =4}$ , llavors ${\displaystyle Q}$ té moment negatiu d'ordre -1 i val Aquesta propietat s'utilitza per a calcular els moments de distribucions de quocients (o ratios) de variables aleatòries independents quan al denominador hi ha una distribució khi quadrat, com en el cas d'una distribució ${\displaystyle t}$ de Student o una distribució ${\displaystyle F}$.

Funció generatriu de moments

La funció generatriu de moments és

Funció característica

La funció característica és

Caràcter reproductiu

Del caràcter reproductiu de les distribucions gamma es dedueix el de les distribucions ${\displaystyle \chi ^{2}}$: Siguin ${\displaystyle Q_{1},\dots ,Q_{n}}$ independents, amb distribucions ${\displaystyle Q_{i}\sim \chi ^{2}(k_{i})}$, ${\displaystyle 1=1,\dots ,n}$. Llavors,

Propietat.:^[3] Siguin ${\displaystyle Q_{1}\sim \chi ^{2}(k_{1})}$ i ${\displaystyle Q_{2}\sim \chi ^{2}(k_{2})}$. Suposem que ${\displaystyle Q=Q_{1}-Q_{2}}$ és independent de ${\displaystyle Q_{2}}$. Aleshores ${\displaystyle Q\sim \chi ^{2}(k_{1}-k_{2})}$.

Aproximació per la distribució normal

En aquesta secció considerarem la distribució ${\displaystyle \chi ^{2}}$ amb un nombre enter de graus de llibertat. D'acord amb el teorema central del límit, si ${\displaystyle Q_{k}\sim \chi ^{2}(k)}$, aleshores

En altres paraules, per a ${\displaystyle k}$ gran, ${\displaystyle Q_{k}}$ és aproximadament normal ${\displaystyle {\mathcal {N}}(k,2k)}$.

Però aquesta aproximació demana ${\displaystyle k}$ força gran. La següent aproximació, deguda a Fisher,^[4] és més ràpida

Equivalentment, per a ${\displaystyle k}$ gran, ${\displaystyle {\sqrt {2Q_{k}}}}$ és aproximadament normal ${\displaystyle {\mathcal {N}}({\sqrt {2k-1}},1)}$ .

Segons Johnson et al^[5] encara és més ràpida l'aproximació deguda a Wilson and Hilferty:^[6] per a ${\displaystyle k}$ gran, ${\displaystyle {\sqrt[{3}]{Q_{k}/k}}}$ és aproximadament normal ${\displaystyle {\mathcal {N}}{\big (}1-{\frac {2}{9k}},{\frac {2}{9k}}{\big )}.}$

La distribució χ² i les mostres de poblacions normals

El següent resultat té una importància fonamental en la inferència estadística basada en mostres de poblacions normals.

Teorema. Sigui ${\displaystyle X_{1},\dots ,X_{n}}$ una mostra d'una població normal ${\displaystyle {\mathcal {N}}(\mu ,\sigma ^{2})}$, és a dir, les variables aleatòries ${\displaystyle X_{1},\dots ,X_{n}}$ són independents i totes tenen distribució ${\displaystyle {\mathcal {N}}(\mu ,\sigma ^{2})}$. Considerem la mitjana mostral $${\displaystyle {\overline {X}}={\frac {1}{n}}\sum _{i=1}^{n}X_{i}.}$$ Aleshores: ${\displaystyle {\frac {1}{\sigma ^{2}}}\sum _{i=1}^{n}{\big (}X_{i}-{\overline {X}}{\big )}^{2}\sim \chi ^{2}(n-1).}$ Les variables aleatòries ${\displaystyle {\overline {X}}}$ i ${\displaystyle \sum _{i=1}^{n}{\big (}X_{i}-{\overline {X}}{\big )}^{2}}$ són independents.

A partir d'aquest teorema i del fet que ${\displaystyle {\overline {X}}\sim {\mathcal {N}}(\mu ,\sigma ^{2}/n)}$, tenim que la variable aleatòria (estadístic)

té una distribució ${\displaystyle t}$ de Sudent amb ${\displaystyle n-1}$ graus de llibertat: ${\displaystyle T\sim t(n-1)}$, on

és la variància mostral.

Relació amb altres distribucions

• Si ${\displaystyle Q_{k}\sim \chi ^{2}(k)}$, aleshores ${\displaystyle Q_{k}}$ té una distribució gamma ${\displaystyle \Gamma {\Big (}{\frac {k}{2}},2{\Big )}}$.
• Si ${\displaystyle Q_{k}\sim \chi ^{2}(k)}$ i ${\displaystyle c>0}$, aleshores ${\displaystyle c\,Q_{k}\sim \Gamma {\Big (}{\frac {k}{2}},2c{\Big )}}$. En particular, per a ${\displaystyle \theta >0}$, tenim que ${\displaystyle {\tfrac {\theta }{2}}Q_{2k}\sim \Gamma (k,\theta )}$. Aquesta propietat és deguda a la propietat d'escala de la distribució gamma.

• Relació amb la distribució de Poisson.^[10]. Sigui ${\displaystyle Q_{k}\sim \chi ^{2}(k)}$ amb ${\displaystyle k}$ parell. Aleshores per a qualsevol ${\displaystyle a>0}$,

on ${\displaystyle Y}$ és una variable aleatòria amb una distribució de Poisson de paràmetre ${\displaystyle a/2}$.

Noteu que aquesta propietat és equivalent a la que es formula a la pàgina de la distribució de Poisson: Si ${\displaystyle Y}$ és una variable amb distribució de Poisson de paràmetre ${\displaystyle \lambda }$, aleshores ^[11] per a ${\displaystyle n=0,\,1,2,\dots }$,

$${\displaystyle P(Y\leq n)=P(Q_{2(n+1)}>2\lambda ),}$$

on ${\displaystyle Q_{2(n+1)}\sim \chi ^{2}{\big (}2(n+1){\big )}}$.

• Si ${\displaystyle Q\sim \chi _{2}^{2}}$, aleshores ${\displaystyle Q}$ té una distribució exponencial de paràmetre 1/2.
• Si ${\displaystyle Q\sim \chi _{2k}^{2}}$, aleshores ${\displaystyle Q}$ té una distribució d'Erlang de paràmetres ${\displaystyle k}$ i 1/2.
• Si ${\displaystyle X\sim \operatorname {Erlang} (k,\lambda )}$ (distribució d'Erlang) llavors ${\displaystyle 2\lambda X\sim \chi ^{2}(2k)}$.
• Si ${\displaystyle X\sim \operatorname {Rayleigh} (1)\,}$ (distribució de Rayleigh) llavors ${\displaystyle X^{2}\sim \chi ^{2}(2)\,}$.
• Si ${\displaystyle X\sim \operatorname {Maxwell} (1)\,}$ (distribució de Maxwell) llavors ${\displaystyle X^{2}\sim \chi ^{2}(3)\,}$.
• Si ${\displaystyle Q_{1}\sim \chi ^{2}(k_{1})\,}$ i ${\displaystyle Q_{2}\sim \chi ^{2}(k_{2})\,}$ són independents, llavors ${\displaystyle Q_{1}/(Q_{1}+Q_{2})\sim \operatorname {Beta} ({\tfrac {k_{1}}{2}},{\tfrac {k_{2}}{2}})\,}$ (Distribució beta).
• Si ${\displaystyle X\sim \operatorname {U} (0,1)\,}$ (distribució uniforme contínua) llavors ${\displaystyle -2\log(X)\sim \chi ^{2}(2)\,}$.

Aplicacions

La distribució khi quadrat té moltes aplicacions en inferència estadística, per exemple en el test khi quadrat i en l'estimació de variàncies. També està involucrada en el problema d'estimar la mitjana d'una població normalment distribuïda i en el problema d'estimar el pendent d'una recta de regressió lineal, a través del seu paper en la distribució t de Student, i participa en tots els problemes d'anàlisi de variància, pel seu paper en la distribució F de Snedecor, que és la distribució del quocient de dues variables aleatòries de distribució khi-quadrat i independents. També té ús al contrast de ${\displaystyle k}$ poblacions amb els contrasts d'homogeneïtat i al d'independència.

Referències

Bibliografia

• Johnson, N. L.; Kotz, S.; Balakrishnan, N. Continuous Univariate Distributions (en anglès). 1 1. 2a edició. Nova York: Wiley, 1994. ISBN 0-471-58495-9. 

Vegeu també

• Distribució gamma
• Distribució exponencial
• Distribució de Poisson
• Prova de khi-quadrat de Pearson
• Distribució multinomial